NIH/NSF (DMS/NIGMS): Geometric flow approach to implicit solvation modeling

A. Progress Statement

As stated in the proposal, current computation of biomolecular solvation faces many fundamental limitations and sever challenges, such as ad hoc assumptions about solvent-solute interfaces to define some of the most important components of the solvation model, and about linear and local solvent response to all solute perturbation. Our goal is to develop geometric flow (i.e., differential geometry) approaches to overcome the abovementioned difficulties in implicit solvent theory and explore the application of the new solvation model. During the last three years, we have investigated novel geometric flow approaches for the solvation analysis of small compounds and biomolecules. We have also developed differential geometry based multiscale models. Applications are considered to viral surface analysis, charge transport in ion channels, proton transport, molecular surface generation. Computational algorithm design and software development are in progress.

B. Studies and Results

[Differential geometry based solvation models]

We have constructed a novel differential geometry based solvation model that starts with a total free energy functional [1, 2]:

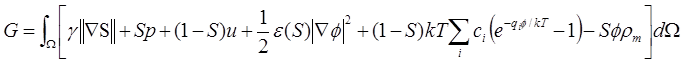
where first three terms are surface energy, mechanical work and solvent-solute interactions, respectively. The rest terms are the electrostatic energy. Here, is the surface tension, S is a surface characteristic function, p is the pressure, is the dielectric function, is the electrostatic potential, k is the Boltzmann constant and T is the temperature, is the bulk concentration of ith ion, and is charge source function of the solute. Coupled generalized Poisson-Boltzmann and geometric flow equations,

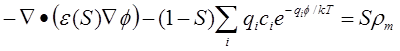
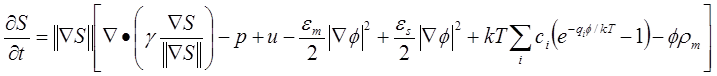
are derived via the variation of the total free energy functional. We would like to quote two anonymous referees’ comments of our manuscript [1] as a summary of this work:

Reviewer #1: The authors present a method for simultaneously computing the electrostatic and 'surface' free energy of a molecule. The approach combines a finite difference Poisson-Boltzmann treatment of the electrostatics with a computational geometry treatment of the molecule: In the latter, the surface bounding the low dielectric interior from the high dielectric solvent is treated through a 3-D functional S, which takes on a value of 1 or 0 in the two regions, and smooth varies between these values in the interface. Then van der Waals, PV and surface free energy terms are introduced as functions of S. The total energy can then be optimized by simultaneous solution of the PB equation and the S dependent energy terms through variation of the phi (potential) and S functionals. This provides a self consistent treatment of the dielectric boundary in the PB and the surface free energy terms.

This is a novel and important advance in the continuum treatment of molecular free energies. The ms. explains the basic ideas clearly and thoroughly, and there is a thorough and systematic exploration of the best way to solve the coupled surface-electrostatic equations numerically. The results are compared to appropriate previous calculations, and the results appear to be very good. This is an excellent piece of work. I only had a few small comments [break].

Fig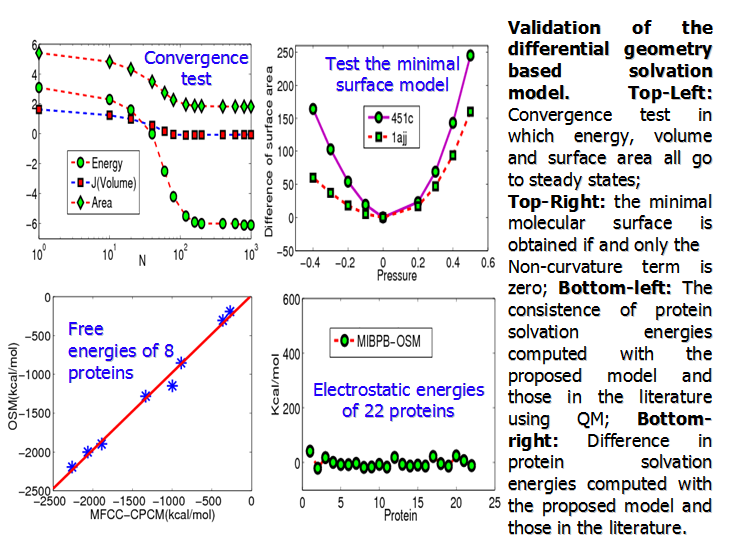

Figure 1. Differential geometry based solvation model [1,2].

Reviewer #2: Synopsis: A novel generalized Poisson-Boltzmann equation is derived, based on total free energy functional that couples polar and non-polar contributions. The formalism also yields a generalized geometric flow equation for construction of realistic solvent-solute boundaries. The new model is tested against experimental solvation free energies of several small molecules, and against QM energies for 22 proteins. Accuracy, stability and robustness issues are thoroughly discussed.

Over-all: this is a very interesting, thorough work. Given the importance of the implicit solvent framework for molecular modeling, and the pressing need for improving its accuracy, this study is very relevant.

Recommendation: Publish with minor (non-mandatory) revisions.

This work has already covered a lot of ground and addressed most of key issues that one would expect in a paper describing a novel method. Addressing additional issues listed below will, in my opinion, strengthen the paper, but should not be considered as mandatory [break].

Figure 2. Surface electrostatic potential [11].

Atomic partial charges are used in our earlier differential geometry based solvation models, which depends on existing molecular mechanical force field software packages for partial charge assignments. As most force field models are parameterized for certain class of molecules or materials, the use of partial charges limits the accuracy and applicability of our earlier models. Moreover, the fixed point charge does not account for the charge rearrangement during the solvation process. The present work proposes a differential geometry based multiscale solvation model which makes use of electron density computed directly from the quantum mechanical principle. We construct a new multiscale total energy functional which consists of not only polar and nonpolar solvation contributions, but also the electronic kinetic and potential energies. By using the Euler-Lagrange variation, we derive a system of three coupled governing equations, i.e., the generalized Poisson-Boltzmann equation for electrostatic potential, the generalized Laplace-Beltrami equation for solvent-solute boundary, and the Kohn-Sham equation for electronic structure. We develop an appropriate iterative procedure to solve three coupled equations and to minimize the solvation free energy. The present multiscale model is numerically validated for its stability, consistency and accuracy. Applications are considered to a few sets of molecules, including a case which is difficult for existing solvation models. Comparison is made with many other classic and quantum models. By using experimental data, we show that the present quantum formulation of our differential geometry based multiscale solvation model improves the prediction of our earlier models, and outperforms some explicit solvation analysis. This work is presented in Ref. [11]

[Differential geometry based nonpolar solvation models]

Nonpolar solvation analysis offers a unique setting to test the validity of solvent-solute interface in the differential geometry based solvation model due to the absence of the interference of electrostatic effects. Many implicit models have been developed for nonpolar solvation analysis. However, their performance is not satisfactory as shown Figure 3. These models rely on unphysical definitions of solvent-solute boundaries. Based on the differential geometry, the present work defines the solvent-solute boundary via the variation of the nonpolar solvation free energy. The solvation free energy functional of the system is constructed based on a continuum description of the solvent and the discrete description of the solute, which are dynamically coupled by the solvent-solute boundaries via dispersion interactions. The first variation of the energy functional gives rise to the governing Laplace-Beltrami equation. The present model predictions of the nonpolar solvation energies are in an excellent agreement with experimental data, which sheds light on the nature of solvent-solute boundaries. This work is presented in Ref. [22].

Figure 3. Differential geometry based nonpolar solvation model [22] gives rise to superb prediction of experimental results.

[Differential geometry based multiscale models]

We have developed a differential geometry based multiscale paradigm to model complex macromolecular systems, and to put macroscopic and microscopic descriptions on an equal footing [3,21]. Large chemical and biological systems such as fuel cells, ion channels, molecular motors, and viruses are of great importance to the scientific community and public health. Typically, these complex systems in conjunction with their aquatic environment pose a fabulous challenge to theoretical description, simulation, and prediction. In our approach, the differential geometry theory of surfaces and geometric measure theory are employed as a natural means to couple the macroscopic continuum mechanical description of the aquatic environment with the microscopic discrete atomistic description of the macromolecule. Multiscale free energy functionals, or multiscale action functionals are constructed as a unified framework to derive the governing equations for the dynamics of different scales and different descriptions. Two types of aqueous macromolecular complexes, ones that are near equilibrium and others that are far from equilibrium, are considered in our formulations. We show that generalized Navier–Stokes equations for the fluid dynamics, generalized Poisson equations or generalized Poisson–Boltzmann equations for electrostatic interactions, and Newton’s equation for the molecular dynamics can be derived by the least action principle. These equations are coupled through the continuum-discrete interface whose dynamics is governed by potential driven geometric flows. Comparison is given to classical descriptions of the fluid and electrostatic interactions without geometric flow basedmicro-macro interfaces. The detailed balance of forces is emphasized in the present work. We further extend the proposed multiscale paradigm to micro-macro analysis of electrohydrodynamics, electrophoresis, fuel cells, and ion channels. We derive generalized Poisson–Nernst–Planck equations that are coupled to generalized Navier–Stokes equations for fluid dynamics, Newton’s equation for molecular dynamics, and potential and surface driving geometric flows for the micro-macro interface. For excessively large aqueous macromolecular complexes in chemistry and biology, we further develop differential geometry based multiscale fluid-electro-elastic models to replace the expensive molecular dynamics description with an alternative elasticity formulation. This work is published in Ref [3] (61 pages) and [21] (55 pages).

[Application to viral surface analysis]

We have developed a differential geometry-based multiscale paradigm to model complex biomolecule systems [4]. Viruses are infectious agents that can cause epidemics and pandemics. The understanding of virus formation, evolution, stability, and interaction with host cells is of great importance to the scientific community and public health. Typically, a virus complex in association with its aquatic environment poses a fabulous challenge to theoretical description and prediction. In our approach, the differential geometry theory of surfaces and geometric measure theory are employed as a natural means to couple the macroscopic continuum domain of the fluid mechanical description of the aquatic environment from the microscopic discrete domain of the atomistic description of the biomolecule. A multiscale action functional is constructed as a unified framework to derive the governing equations for the dynamics of different scales. We show that the classical Navier-Stokes equation for the fluid dynamics and Newton’s equation for the molecular dynamics can be derived from the least action principle. These equations are coupled through the continuum-discrete interface whose dynamics is governed by potential driven geometric flows.

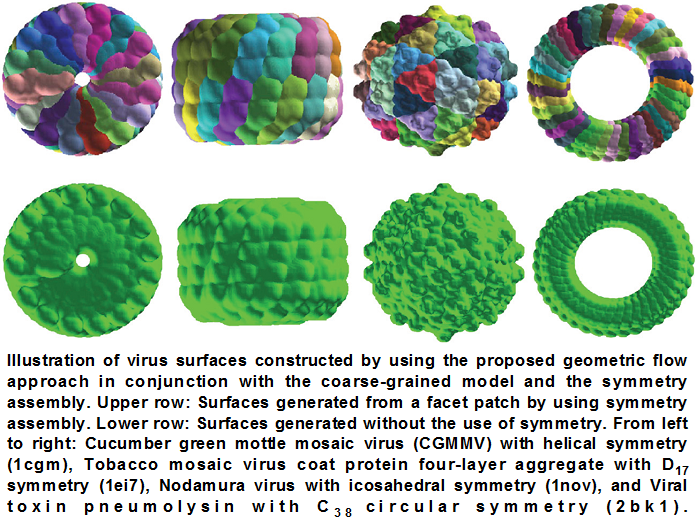
Figure 4. Virus surfaces [4].

[Application to ion transport in ion channels]

The Poisson Nernst-Planck (PNP) model is based on a mean-field approximation of ion interactions and continuum descriptions of concentration and electrostatic potential. It provides qualitative explanation and increasingly quantitative predictions of experimental measurements for the ion transport problems in many areas such as semiconductor devices, nanofluidic systems and biological systems, despite of many limitations. However, in the PNP model, the number of equations to be solved and the number of diffusion coefficient profiles to be determined for the calculation directly depend on the number of ion species in the system, since each ion species corresponds to one Nernst-Planck equation and one position-dependent diffusion coefficient profile. In a complex system with multiple ion species, the PNP can be computationally expensive and parameter demanding, as experimental measurements of diffusion coefficient profiles are generally quite limited for most confined regions such as ion channels, nano-structures and nanopores. We propose an alternative model to reduce number of Nernst-Planck equations to be solved in complex chemical and biological systems with multiple ion species by substituting Nernst-Planck equations with Boltzmann distributions of ion concentrations. As such, we solve the coupled Poisson-Boltzmann and Nernst-Planck (PBNP) equations, instead of the PNP equations. The proposed PBNP equations are derived from a total energy functional by using the variational principle. We design a number of computational techniques, including the Dirichlet to Neumann mapping, the matched interface and boundary (MIB), and relaxation based iterative procedure, to ensure efficient solution of the proposed PBNP equations. Two protein molecules, cytochrome c551 and Gramicidin A, are employed to validate the proposed model under a wide range of bulk ion concentrations and external voltages. Extensive numerical experiments show that there is an excellent consistence between the results predicted from the present PBNP model and those obtained from the PNP model in terms of the electrostatic potentials, ion concentration profiles, and current-voltage (I-V) curves. The present PBNP model is further validated by a comparison with experimental measurements of I-V curves under various ion bulk concentrations. Numerical experiments indicate that the proposed PBNP model is more efficient than the original PNP model in terms of simulation time. This work is published in Ref. [8].

Figure 5. Ion channel model [8,10]. Upper left: Gramicidin A channel; Upper right: Electrostatic surface potential of the Gramicidin A protein; Bottom left: The projection of the electrostatic potential along the channel axis. Bottom right: Voltage-Current relations compared with experimental data for the Gramicidin A channel.

[Application to proton transport in ion channels]

Proton transport plays an important role in biological energy transduction and sensory systems. Therefore it has attracted much attention in biological science and biomedical engineering in the past few decades. The present work proposes a multiscale/multiphysics model for the understanding of the molecular mechanism of proton transport in transmembrane proteins involving continuum, atomic and quantum descriptions, assisted with the generation and visualization of membrane channel surfaces. We describe proton dynamics quantum mechanically via a new density functional theory based on the Boltzmann statistics, while implicitly model numerous solvent molecules as a dielectric continuum to reduce the number of degrees of freedom. The density of all other ions in the solvent is assumed to obey the Boltzmann distribution. The impact of protein molecular structure and its charge polarization on the proton transport is considered explicitly at the atomic scale. A variational solute-solvent interface is designed to separate the explicit molecule and implicit solvent regions. We formulate a total free energy functional to put proton kinetic and potential energies, free energy of all other ions, polar and nonpolar energies of the whole system on an equal footing. The variational principle is employed to derive coupled governing equations for the proton transport system. Generalized Laplace-Beltrami equation, generalized Poisson-Boltzmann equation and generalized Kohn-Sham equation are obtained from the present variational framework. The variational solvent-solute interface is generated and visualized to facilitate the multiscale discrete/continuum/quantum descriptions. Theoretical formulations for the proton density and conductance are constructed based on fundamental laws of physics. A number of mathematical algorithms, including the Dirichlet to Neumann mapping (DNM), matched interface and boundary (MIB) method, Gummel iteration, and Krylov space techniques are utilized to implement the proposed model in a computationally efficient manner. The Gramicidin A (GA) channel is used to validate the performance of the proposed proton transport model and demonstrate the efficiency of the proposed mathematical algorithms. The proton channel conductance is studied over a number of applied voltages and reference concentrations. A comparison with experimental data verifies the present model predictions and confirms the proposed model. This modeling and computation of proton transport are developed in Refs [12, 13,20] .

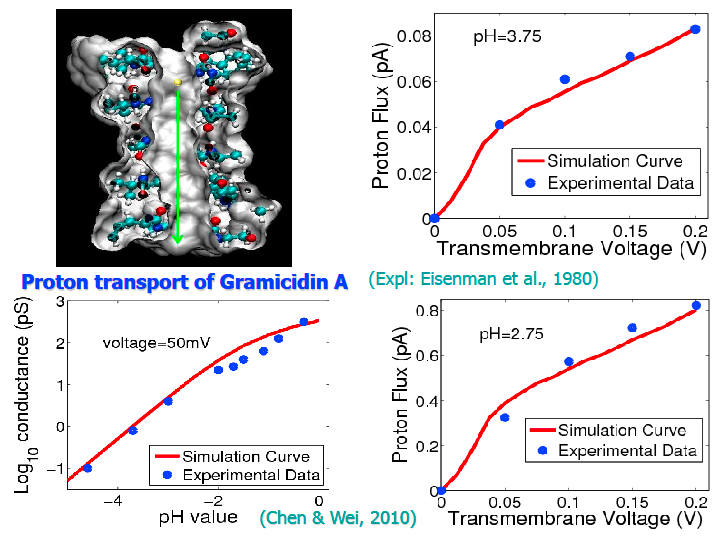
Figure 6. Simulation and comparison with experimental data for proton transport in the Gramicidin A channel [12,13,20].

[Application to electron transport in nano-devices]

The miniaturization of nano-scale electronic devices, such as metal oxide semiconductor field effect transistors (MOSFETs), has given rise to a pressing demand in the new theoretical understanding and practical tactic for dealing with quantum mechanical effects in integrated circuits. Modeling and simulation of this class of problems have emerged as an important topic in applied and computational mathematics. Based on the mathematical framework developed in our solvation analysis, we presents mathematical models and computational algorithms for the simulation of nano-scale MOSFETs. We introduce a unified two-scale energy functional to describe the electrons and the continuum electrostatic potential of the nano-electronic device. This framework enables us to put microscopic and macroscopic descriptions in an equal footing at nano scale. By optimization of the energy functional, we derive consistently-coupled Poisson-Kohn-Sham equations. Additionally, layered structures are crucial to the electrostatic and transport properties of nano transistors. A material interface model is proposed for more accurate description of the electrostatics governed by the Poisson equation. Finally, a new individual dopant model that utilizes the Dirac delta function is proposed to understand the random doping effect in nano electronic devices. Two mathematical algorithms, the matched interface and boundary (MIB) method and the Dirichlet-to-Neumann mapping (DNM) technique, are introduced to improve the computational efficiency of nano-device simulations. Electronic structures are computed via subband decomposition and the transport properties, such as the I-V curves and electron density, are evaluated via the non-equilibrium Green's functions (NEGF) formalism. Two distinct device configurations, a double-gate MOSFET and a four-gate MOSFET, are considered in our three-dimensional numerical simulations. For these devices, the current fluctuation and voltage threshold lowering effect induced by the discrete dopant model are explored. Numerical convergence and model well-posedness are also investigated in the present work. This work is published in Ref. [6]

[Application to fast molecular surface generation]

We introduce a new framework for the surface generation based on the partial differential equation (PDE) transform, which utilizes high order geometric evolution equations. The PDE transform has recently been introduced by us as a general approach for the mode decomposition of images, signals, and data. It relies on the use of arbitrarily high-order PDEs to achieve the time–frequency localization, control the spectral distribution, and regulate the spatial resolution. The present work provides a new variational derivation of high-order PDE transforms. The fast Fourier transform is utilized to accomplish the PDE transform so as to avoid stringent stability constraints in solving high-order PDEs. As a consequence, the time integration of high-order PDEs can be done efficiently with the fast Fourier transform. The present approach is validated with a variety of test examples in two-dimensional and three-dimensional settings. We explore the impact of the PDE transform parameters, such as the PDE order and propagation time, on the quality of resulting surfaces. Additionally, we utilize a set of 10 proteins to compare the computational efficiency of the present surface generation method and a standard approach in Cartesian meshes. Moreover, we analyze the present method by examining some benchmark indicators of biomolecular surface, that is, surface area, surface-enclosed volume, solvation free energy, and surface electrostatic potential. A test set of 13 protein molecules is used in the present investigation. The electrostatic analysis is carried out via the Poisson–Boltzmann equation model. To further demonstrate the utility of the present PDE transform-based surface method, we solve the Poisson–Nernst–Planck equations with a PDE transform surface of a protein. Second-order convergence is observed for the electrostatic potential and concentrations. Finally, to test the capability and efficiency of the present PDE transform-based surface generation method, we apply it to the construction of an excessively large biomolecule, a virus surface capsid. Virus surface morphologies of different resolutions are attained by adjusting the propagation time. Therefore, the present PDE transform provides a multiresolution analysis in the surface visualization. Extensive numerical experiment and comparison with an established surface model indicate that the present PDE transform is a robust, stable, and efficient approach for biomolecular surface generation in Cartesian. This work is described in Ref. [19]

[Application to mode decomposition]

The geometry flow formalism proposed in the present work is utilized to develop a new method for the mode decomposition [15,16,17]. This new method is called partial differential equation (PDE) transform [15]. Like the wavelet transform, the PDE transform is able to decompose signals, images and data into functional modes, such as edges, trend, texture and feature with controllable frequency ranges and time-frequency localizations, which correspond to appropriate multiresolution analysis in the physical domain. Similarly, the PDE transform also has a prefect reconstruction of original signals, images and data. The PDE transform has found its success in signal processing [16,17], biomedical image analysis [15] and biomolecular surface construction and visualization [19].

[Computational algorithms]

Computational methods and algorithms are designed and developed for the solution of the generalized Poisson-Boltzmann equation and generalized geometric flow equations [1,2]. Specifically, a second-order finite difference scheme is designed to solve the generalized Poisson-Boltzmann equation. The effect of the appropriate preconditioner to the basic Poisson-Boltzmann solver is explored. Both a simpleminded Euler method and an appropriate alternative direction implicit (ADI) scheme are constructed to solve the nonlinear generalized geometric flow equation. The ADI scheme allows a relatively large time stepping and provides better efficiency. Finally, two iterative approaches are designed and tested for the solution of the coupled Poisson-Boltzmann equation and the generalized geometric flow equation. All computational methods have been extensively validated [1,2].

Second order convergent numerical method has been developed to solve the Poisson-Nernst-Planck (PNP) equations against complex protein surfaces, geometric singularities, and singular delta functions [10]. This is the first second order solver for the PNP equations in biomolecular context.

The matched interface and boundary (MIB) developed in Wei’s lab has been further studied to account for solving the Poisson-Boltzmann equation with multiple material interfaces, which occur in implicit solvation models when metal active centers exist. This is the first time the second order convergent numerical method has been constructed for this class of problems. This work is described in Refs. [9,14].

We have been putting effort on the development of efficient computational methods and software packages for the biophysical and biochemistry communities. The MIBPB package described in our recent paper [5] has been further improved by considering a full scope of topological variations in complex biomolecules. Previously, geometric singularities of large proteins may cause a stop of our algorithm, although on a rare basis. We have fixed the algorithm problem and developed a robust interface technique based Poisson-Boltzmann solver package.

We are developing a finite element version of our MIB method and comparing this approach with our earlier finite difference based MIB. A three-dimensional MIB Galerkin method is under construction. Part of our work is described in Refs. [24,25].

[Software development]

We have developed a software package for the solution of the Poisson-Boltzmann equation [5]. The Poisson-Boltzmann equation (PBE) is an established model for the electrostatic solvation analysis of biomolecules. The development of advanced computational techniques for the solution of the PBE has been an important topic in the past two decades. This work presents a matched interface and boundary (MIB) based PBE software package, the MIBPB solver, for electrostatic analysis. The MIBPB has a unique feature that it is the first interface technique based PBE solver that rigorously enforces the solution and flux continuity conditions at the dielectric interface between the biomolecule and the solvent. For protein molecular surfaces which may possess troublesome geometrical singularities, the MIB scheme makes the MIBPB by far the only existing PBE solver that is able to deliver the second order convergence, i.e., the accuracy increases four times when the mesh size is halved. The MIBPB method is also equipped with a Dirichlet-to-Neumann mapping (DNM) technique, that builds a Green's function approach to analytically resolve the singular charge distribution in biomolecules in order to obtain reliable solutions at meshes as coarse as 1 while it usually takes other traditional PB solvers 0.25to reach similar level of reliability. The present work further accelerates the rate of convergence of linear equation systems resulting from the MIBPB by utilizing the Krylov subspace (KS) techniques. Condition numbers of the MIBPB matrices are signi_cantly reduced by using appropriate Krylov subspace solver and preconditioner combinations. Both linear and nonlinear PBE solvers in the MIBPB package are tested by protein-solvent solvation energy calculations and analysis of salt effects on protein-protein binding energies, respectively.

[Report from Nathan Baker group]

• We received the FORTRAN code from Zhan and Guowei Wei in January 2011 and slightly modified it to implement appropriate interaction potentials and non-polar free energy.

• In a paper recently submitted to Journal of Computational Chemistry [26], we have developed a new parameterization scheme for our geometric flow approach.  Implicit solvent models are popular for their high computational efficiency and simplicity over explicit solvent models and are extensively used for computing molecular solvation properties.  The accuracy of implicit solvent models depends on the geometric description of the solute-solvent interface and the solvent dielectric profile that is defined near the surface of the solute molecule.  Typically, it is assumed that the dielectric profile is spatially homogeneous in the bulk solvent medium and varies sharply across the solute-solvent interface.  However, the specific form of this profile is often described by ad hoc geometric models rather than physical solute-solvent interactions.  Hence, it is of significant interest to improve the accuracy of these implicit solvent models by more realistically defining the solute-solvent boundary within a continuum setting.  Recently, a differential geometry-based geometric flow solvation model was developed, in which the polar and nonpolar free energies are coupled through a characteristic function that describes a smooth dielectric interface profile across the solvent–solute boundary in a thermodynamically self-consistent fashion.  The main parameters of the model are the solute/solvent dielectric constants, solvent pressure on the solute, microscopic surface tension, solvent density, and molecular force-field parameters.  In this work, we investigate how changes in the pressure, surface tension, and choice of different force-field charge and radii parameters affect the prediction accuracy for hydration free energies of 17 small organic molecules based on the geometric flow solvation model.  These results are highlighted in the following Figure 7 and provide insights on the parameterization, accuracy, and predictive power of this new implicit solvent model.

Figure 7. Solvation errors for 17 small molecules generated by new parameterizations of the differential geometry based solvation model by Baker’s group.

C. Future Plan

In our future plan, we will explore a number of fronts. The first is to further advance the application of the present geometric flow framework to geometric and topological modeling of biomolecular systems. Additionally, we will construct differential geometry based models and methods for nanofluidic systems. Finally, we will continue our computational algorithm and software development.

First, geometric modeling and topological modeling of macromolecular systems are important tasks in structural biology and molecular biology. The differential geometry based methods and techniques developed in the present work can play a crucial role in such modeling. The essential idea is to combine geometric flow evolution equations to improve the quality of biomolecular data collected by the Cryo Electron Microscopy, which is of low resolution and often corrupted with noise. The experience learned from the present project will enable us to do an excellent job in geometric and topological modeling of macromolecules, including improved meshing, a better estimation of area and volume, robust calculation of curvature, genus number, and Frenet frame.

Additionally, nano-fluidics is a fast-growing nano-bio technology. It has been applied to a wide range of chemical and biological systems, including DNA sequencing, PCR, separation of protein-antibody, membrane protein crystallization, etc. Most current theories describe only the flow effect, but ignore the electrostatic interactions. A multiscale model has been proposed in our recent work [3]. One of our future interests is to carry detail numerical analysis and simulation of nanofluidic systems by using the proposed differential geometry based multiscale models.

The Baker group will continue making contribution to solvation modeling and software development. The newly developed differential geometry based solvation codes will be integrated with the popular software tools developed in the Baker group, such as APBS and PDB2PQR. This development will ensure that the results obtained from this NIH grant will be immediately available to the computational biology community.

Peter Bates will continue his effort in the mathematical analysis of the proposed coupled Poisson-Boltzmann and geometric flow equations. Mathematical analysis usually follows a different path. Its progress is normally slow, but runs deep. We expect that our future mathematical analysis will lead to better understanding of theoretical and computational aspects of the proposed multiscale solvation models.

D. Publication

1. Zhan  Chen,  Nathan Baker  and G. W.  Wei, Differential  geometry  based solvation model I:  Eulerian formulation, Journal of Computational Physics, 229, 8231-8258 (2010). NIHMSID#215329

2. Zhan  Chen,  Nathan Baker  and G. W.  Wei, Differential  geometry  based solvation  model II: Lagrangian  formulation, Journal of Mathematical biology, in press (2011). NIHMSID#215331

3. Guo-Wei, Wei, Differential geometry  based multiscale models, Bulletin of Mathematical Biology, volume 72, 1562-1622,  (2010). NIHMSID# 215327 http://www.springerlink.com/content/8303641145x84470/fulltext.pdf

4. Changjun Chen, Rishu Saxena, and Guo-Wei Wei, Differential geometry based multiscale model for virus capsid dynamics, Int. J. Biomed Imaging, Volume 2010, Article ID 308627, 308627, 9 pages (2010). (NIHMSID#215328 http://www.hindawi.com/journals/ijbi/2010/308627.html

5. Duan Chen, Zhan  Chen, Changjun  Chen, Weihua Geng and Guo-Wei Wei,  MIBPB: A software package for electrostatic analysis, Journal of computational Chemistry, 32, 756–770 (2011). NIHMSID#215330

6. Duan Chen and Guo-Wei Wei, Modeling and simulation of nano-electronic devices, Journal of Computational Physics, 229, 4431-4460, (2010). NIHMSID#181011

7. Weihua Geng and G.W. Wei, Multiscale molecular dynamics via the matched interface and boundary (MIB) method, Journal of Computational Physics, 230, 435-457 (2011). NIHMSID#243881

8. Qiong Zheng and Guo-Wei Wei, Poisson-Boltzmann-Nernst-Planck model. Journal of Chemical Physics, 134 (19), 194101, (2011). NIHMSID#298927

9. Kelin Xia, Meng Zhan and Guo-Wei Wei, The matched interface and boundary (MIB) method for multi-domain elliptic interface problems. Journal of Computational Physics , 230, 8231–8258 (2011). NIHMSID#281679

10. Qiong Zheng, Duan Chen and Guo-Wei Wei, Second-order Poisson-Nernst-Planck solver for ion transport. Journal of Computational Physics, 230, 5239-5262 (2011). NIHMSID#286113

11. Zhan Chen and G. W. Wei, Differential geometry based salvation model III: Quantum formulation, Journal of Chemical Physics, 135, 194108 (2011). NIHMSID#374656

12. Duan Chen, Zhan Chen and Guo-Wei Wei, Quantum dynamics in continuum models for proton transport II: Variational solvent-solute interface, International  Journal for Numerical    Methods in Biomedical  Engineering, 28, 25-51 (2012). PMCID: PMC3274368

13. Duan Chen and Guo-Wei Wei, Quantum dynamics in    continuum models for  proton transport I:  Basic formulation, Communication  in Computational Physics,    in press (2012). NIHMSID #374856

14. Kelin Xia, Meng Zhan, Decheng Wan and Guo-Wei Wei, Adaptively deformed mesh based interface method for elliptic equations with discontinuous coefficients, Journal of Computational  Physics, 231, 1440–1461 (2012). NIHMSID# 374658

15. Yang Wang, Guo-Wei Wei and Siyang Yang, Partial differential equation transform --- variational formulation and Fourier analysis , International Journal for Numerical Methods in Biomedical Engineering, 27, 1996-2020, (2011). NIHMSID#298929

16. Yang Wang, Guo-Wei Wei and Siyang Yang, Model decomposing  evolution equations, Journal  of Scientific Computing,    50, 495-518 (2012). PMCID: PMC3293488

17. Yang Wang, Guo-Wei Wei and Siyang Yang, Iterative filtering decomposition    using local spectral    evolution kernels, Journal  of Scientific Computing,   50, 629-664 (2012), PMCID: PMC3281768

18. Yang Wang,    Guo-Wei    Wei and Siyang    Yang, Selective    extraction of entangled  textures via adaptive  PDE transform, Int.      J. Biomed Imaging,    Volume 2012 (2012), Article ID 958142(2012). PMCID: PMC3272340

19. Qiong  Zheng,    Siyang    Yang and Guo-Wei    Wei, Molecular surface    generation    using PDE transform.    International  Journal  for Numerical Methods in Biomedical Engineering,  28, 291-316   (2012). NIHMSID#329786

20. Duan Chen  and Guo-Wei Wei,    Quantum dynamics in    continuum models for    proton transport ---    Generalized correlation, Journal of Chemical Physics,  136, 134109 (2012) NIHMSID#256945

21. G.W. Wei, Zhan  Chen, Kelin Xia and  Qiong Zheng, Variational multiscale models for  charge transport, SIAM review. In press (2012). NIHMSID#367755

22. Zhan Chen,    Shan Zhao, Jaehun Chun, Dennis G. Thomas, Nathan    Baker, Peter Bates  and Guo-Wei Wei,  Variational    multiscale    approach for nonpolar    solvation analysis, (2012).   NIHMSID#374673

23. Langhua Hu    and  Guo-Wei    Wei, Nonlinear Poisson    equation for inhomogeneous  media. (2012).

24. Kelin  Xia, Meng Zhan, and    Guo-Wei   Wei, MIB Galerkin  for elliptic interface  problems (2012).

25. L. Mu, J. P. Wang,  G. W. Wei, X. Ye  and S.Zhao, Weak Galerkin methods for  second order elliptic  interface problems. (2012)

26. Dennis G. Thomas, Jaehun Chun, Zhan Chen, Guowei Wei, Nathan A. Baker, Parameterization of a Geometric Flow Implicit Solvation Model, submitted to Journal of Computational Chemistry. (2012)