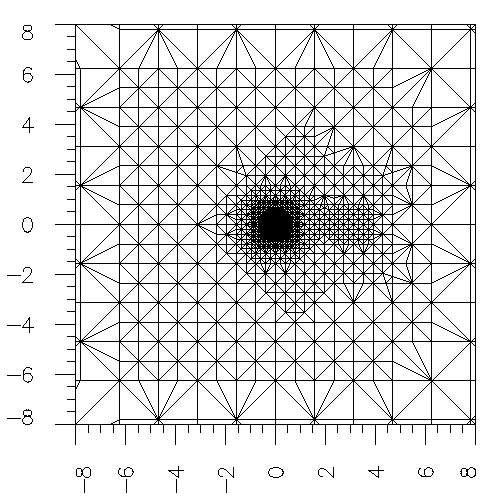Adaptive Numerical Methods for Electronic Structure Calculation
My current research focuses on the finite element method for time-dependent density functional theory(TDDFT), and time-dependent current density functional theory(TDCDFT).
In our previous work, the adaptive finite element methods are studied for solving the Kohn-Sham equation, and the results are reported in this paper and this paper. In the former paper, a harmonic based mesh redistribution method is introduced to realize the adaptive finite element implementation, which successfully improve the efficiency and the numerical accuracy of the results, without increasing the mesh grids. In the later one, the mesh local refinment and/or coarsening method is studied for solving the Kohn-Sham equation by the finite element method. Compared with the mesh redistribution method, the mesh regularity can be kept well by the local refinement technique. Although the mesh regularity can also be kept by the mesh redistribution locally, see the result in that paper, it is not trivial for keeping it globally, which we believe is not a desired property for a multiscale simulation in the future.
Based on our previous results, recently, we are working on the numerical simulation of time-dependent density functional theory by the finite element method with a time propagation way. It is known that there are two ways to run a TDDFT simultion, say, using the linear response theory and using a time propagation method. Although it is very computationally demanding for a time propagation method, it is almost only way to study the nonlinear phenomenon, which make an efficient numerical method very important. The related results will be reported in our forthcoming paper.
All our numeircal experiments are implemented by a C++ library AFEABIC(Adaptive Finite Element package for the AB-Initio Calculations) which is still under development.
The following are some results from AFEABIC.
The simulation of the ground state of the molecule Lithium Hydride. Right figure shows the sliced mesh on the X-Y plane. The whole domain is chosen as a cube with size [-100,100]x[-100,100]x[-100,100], and the atomic unit is used. The all-electron calculation is implemented for this simulation. The figure shows that the mesh elements in the vicinity of the lithium nucleus and hydrogen nucleus are successfully refined. The chemical bond of Li-H can also be observed obviously from the mesh. That means our adaptive mesh refinement method works very well.
The same simulation to the above one. The isosurface of the electron density is demonstrated in the left figure.
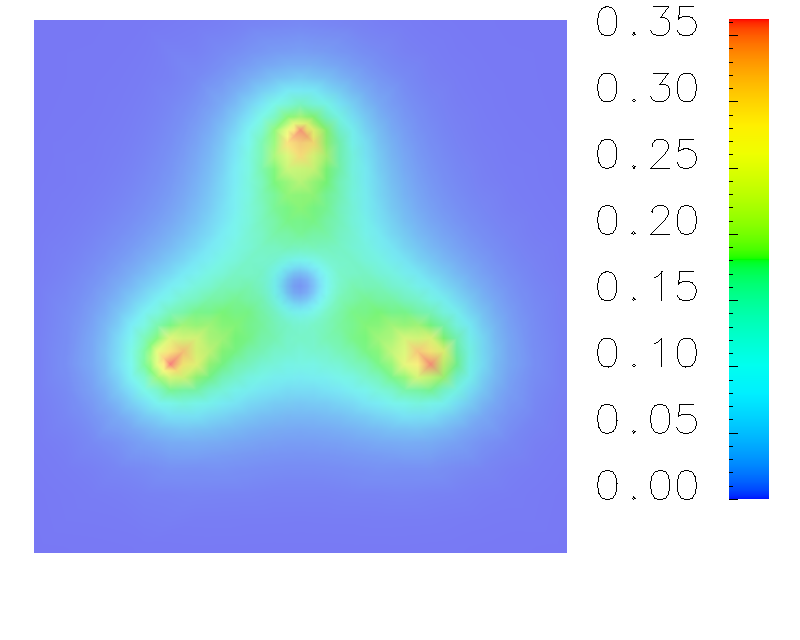
The simulation of the ground state of borane (BH3). The isosurface of the electron density in the X-Y plane is demonstrated in the right figure. In this simulation, [-100,100]x[-100,100]x[-100,100] domain size is used, and atomic unit is chosen. The Troullier-Martin norm-conserving pseudo-potential is adopted for boron atom, and all-electron calculation is implemented for three hydrogen atoms. The Kleinman-Bylander form is used for the pseudo-potential form, and s-orbital works as the local part in KB form. From the right figure, we can see the high electron density distributes in the vicinity of three hydrogen nucleii, and three B-H bonds can be observed easily.
This is an all-electron calculation for diborane molecule (B2H6).
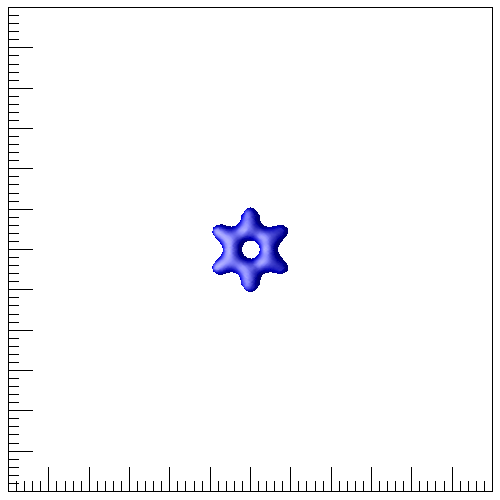
This is a pseudopotential simulation of a benzene (C6H6) molecule. The bond length data are from Octopus.
Computational Fluid Dynamics
In this research work, we focus on the simulation of the compressible flow. More specifically, we are working on the efficient numerical method for solving the steady state Euler equations. The study on the steady state of the Euler equations is very meaningful on, for example, the shape design of a car, an airfoil, etc.. However, it is not trivial for developing efficient numerical methods for solving the steady Euler equations because of its nonlinearity, and the complexity of the practical configurations.
In this paper, the authors proposed a numerical framework, which is based on the finite volume methods, for solving the steady state Euler equations. The framework consists of the Newton method and a geometrical multi-grid method, which is proved very efficient and robust in their paper. Based on this work, we introduced a WENO recontruction method for the solution reconstruction in this paper to improve the solution quality, which worked very well in the implementation. Besides removing the nonphysical oscillation, our WENO reconstruction method also positively affects the convergence of the Newton iteration. Based on a hierarchical idea, we extend the numerical method to the third order case. See this paper for the results. The related results can also be found in my PhD Thesis.
Recently, a paper on the extension of the numerical method to the adaptive case has been accepted. In this work, different reconstruction patches are tested carefully in WENO reconstruction method, for uniform and adaptive refinement, respectively. Also, an appropriate parameter $p$ in WENO recontruction is given by our numerical experience. The perfornamce of each patch and parameter is demonstrated, and the reason behind these performances are discussed detailedly. In the paper, an indicator for adaptive refinement is developed by using the entropy production of the numerical method. The details on why and how to generate such indicator is introduced in the paper.