I work in several connected areas of mathematics: complex and harmonic analysis, geometric measure theory, and elliptic partial differential equations. Here are some brief overviews of the projects I have been working on, as well as those I am currently involved in. More information can be found in my
curriculum vitae or
on arXiv.
- My main topic has been about the size (in the sense of Hausdorff measure) of the sets where a given quasiconformal map can distort in a prescribed manner involving stretching and rotation. By varying a construction of Uriarte-Tuero to sharpen a result of Hitruhin and show that these distortion sets can be very large; this work is written up in this preprint.
- I have also worked on Holder continuity of quasiconformal maps. This is related to some deep questions - for example, it is an open problem to find a (general) way of detecting when a solution to a Beltrami equation is bilipschitz. This is also related to the connectivity of the manifold of chord-arc domains. I am currently studying estiamtes of the Holder exponent from certain local averages of the Beltrami coefficient.
- I have also studied Favard length and Buffon needle problems in the plane. I have developed new techniques and estimates that apply to some classes of self-similar sets; these can be used to give bounds for average lengths of sets. A preprint of this can be found here.
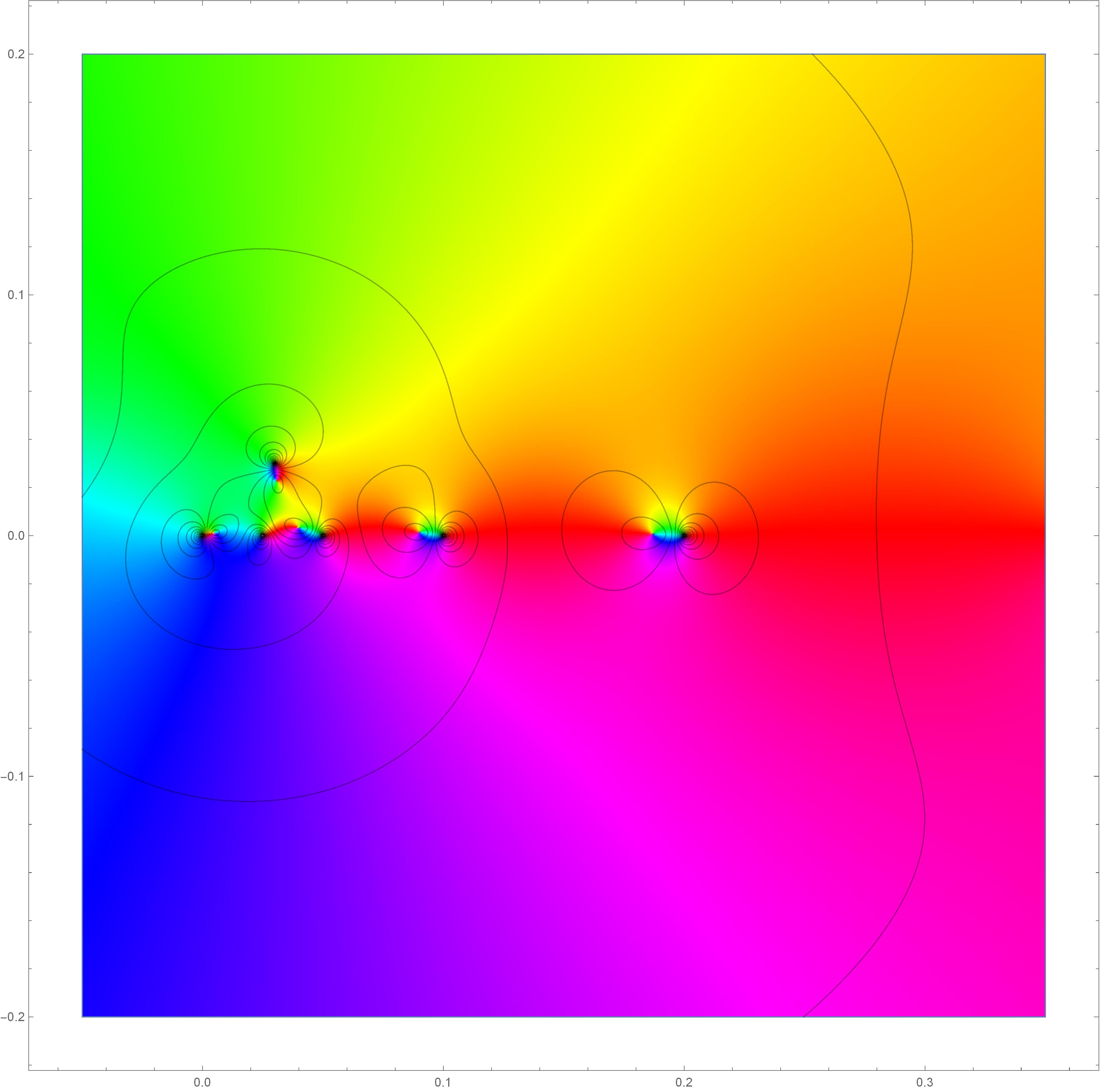Visualization of complex mapping with complicated stretching and rotation