I work in several connected areas of mathematics: complex and harmonic analysis, geometric measure theory, and elliptic partial differential equations. Here are some brief overviews of the projects I have been working on, as well as those I am currently involved in. More information can be found in my
curriculum vitae or
on arXiv.
- My main topic has been about the size (in the sense of Hausdorff measure) of the sets where a given quasiconformal map can distort in a prescribed manner involving stretching and rotation. By varying a construction of Uriarte-Tuero to sharpen a result of Hitruhin and show that these distortion sets can be very large; this work is written up in this preprint.
- I have also worked on Holder continuity of quasiconformal maps. This is related to some deep questions - for example, it is an open problem to find a (general) way of detecting when a solution to a Beltrami equation is bilipschitz. This is also related to the connectivity of the manifold of chord-arc domains. I am currently studying estiamtes of the Holder exponent from certain local averages of the Beltrami coefficient.
- I have also studied Favard length and Buffon needle problems in the plane. I have developed new techniques and estimates that apply to some classes of self-similar sets; these can be used to give bounds for average lengths of sets. A preprint of this can be found here.
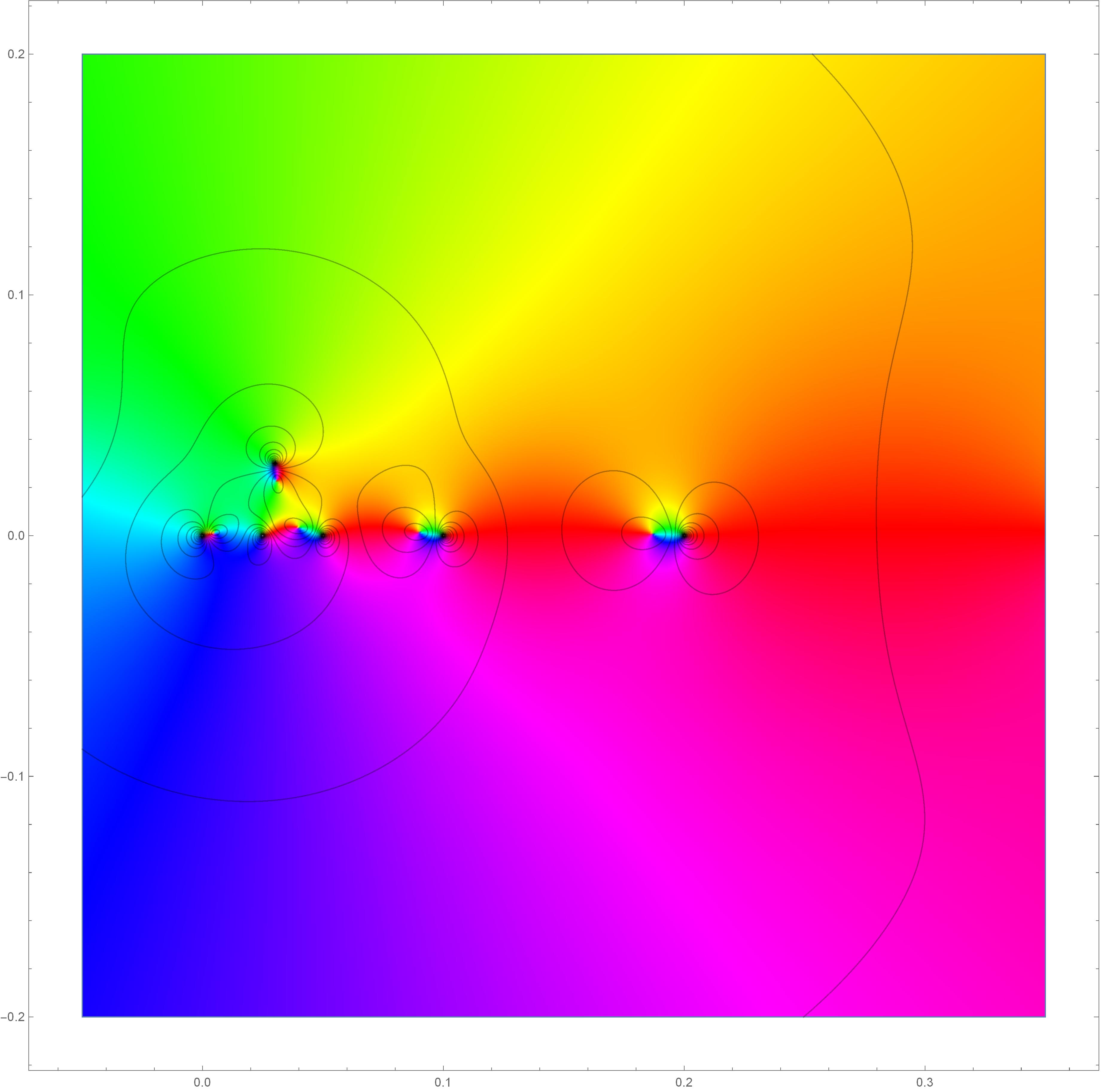 Visualization of complex mapping with complicated stretching and rotation
Visualization of complex mapping with complicated stretching and rotation
 Visualization of complex mapping with complicated stretching and rotation
Visualization of complex mapping with complicated stretching and rotation