My research interests lie at the intersection of applied mathematics, signal processing and scientific computing. In particular, I am interested in problems in applied and computational harmonic analysis, as well as numerical methods for large-scale scientific computing problems. These interests are motivated in part by data-driven applications in bio-medical and molecular imaging, signal processing and communication systems, as well as model-driven applications such as wave propagation and computational electromagnetics.
This page summarizes my current research interests as well as research problems I have worked on previously.
Phase Retrieval
At the heart of molecular imaging modalities such as X-ray crystallography lies a fascinating and equally challenging mathematical problem – the phase retrieval problem – which involves the reconstruction of signals from phaseless (or magnitude-only) measurements. These measurements typically arise due to the underlying physics of the problem. For example, in X-ray crystallography, the acquired diffraction pattern corresponds to the squared magnitude of the Fourier transform of the specimen being imaged. Since the phase encodes a significant amount of structure in the underlying signal, phase retrieval is an incredibly challenging problem.
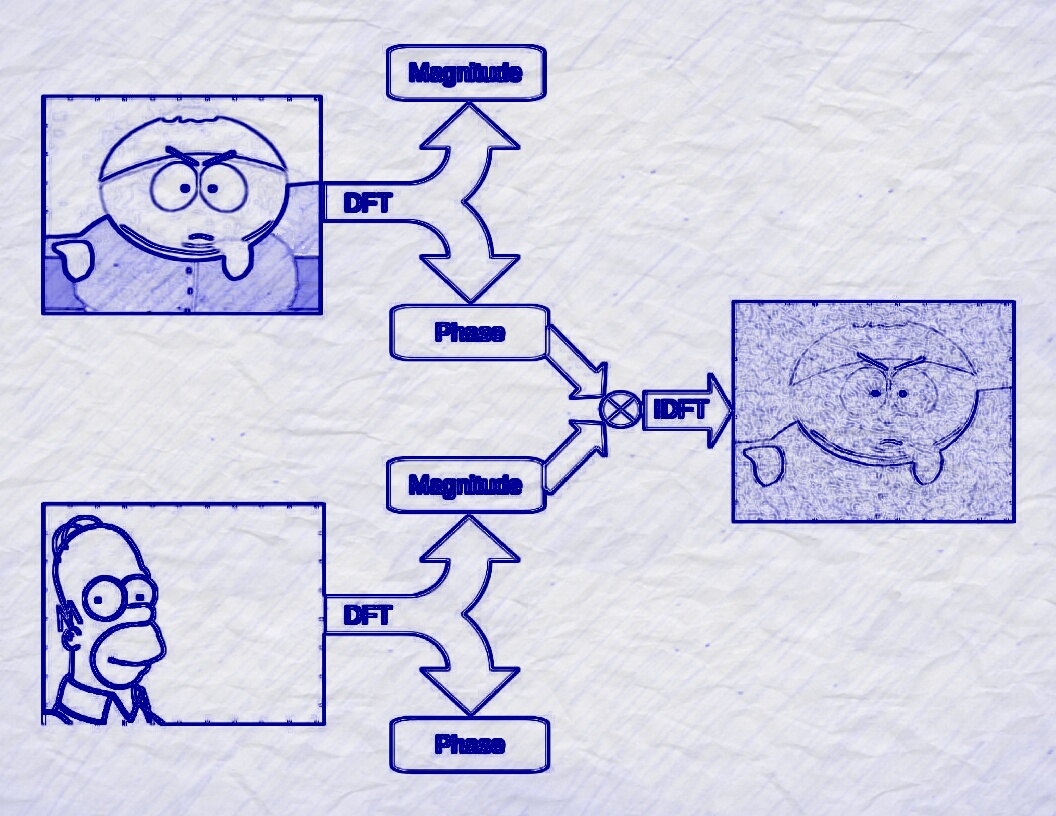
My specific interests are in developing highly efficient (essentially linear time), provably accurate, and noise-robust algorithms for reconstructing one- and multi-dimensional signals from phaseless measurements. Of particular interest are algorithms and associated deterministic measurement constructions relevant to Ptychographic imaging - a modern variant of X-ray crystallography which employs local Fourier-based magnitude measurements.
I am also interested in fast (sublinear-time), accurate and robust compressive phase retrieval algorithms which use an optimal (linear-in-sparsity) number of measurements.
Related Material:
- Phase retrieval from local correlation measurements [preprint]
- Fast compressive phase retrieval [preprint]
- Some slides summarizing the method and main results
- Matlab code implementing these algorithms:
- Phase Retrieval [BlockPR]
- Compressive Phase Retrieval [SparsePR]
Collaborators: Mark Iwen (Michigan State University), Yang Wang (Hong Kong University of Science and Technology), Rayan Saab (University of California, San Diego).
Reconstruction from Fourier Data
Certain applications such as magnetic resonance imaging (MRI) require the reconstruction of functions or features (such as edges) from Fourier spectral data. In these applications, the acquired measurements are often noisy, sparsely sampled and sometimes collected along non-uniform sampling trajectories (see alongside). Accurate and efficient reconstruction as well as feature detection from such data is a non-trivial task, with the mathematical and computational challenge amplified by the piecewise-smooth nature of real-world functions. The intricate interplay between local features (such as edges) and global expansions (the Fourier measurements) is what makes such problems, in equal parts, intriguing and formidable.
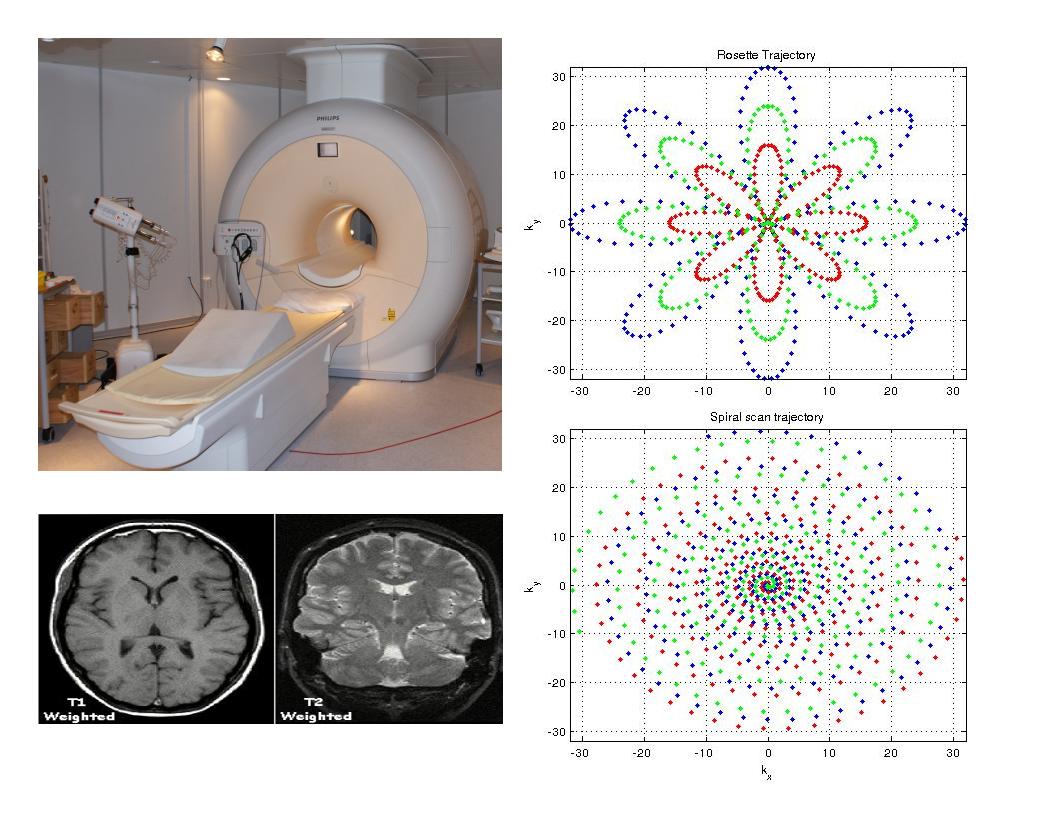
My current interests include
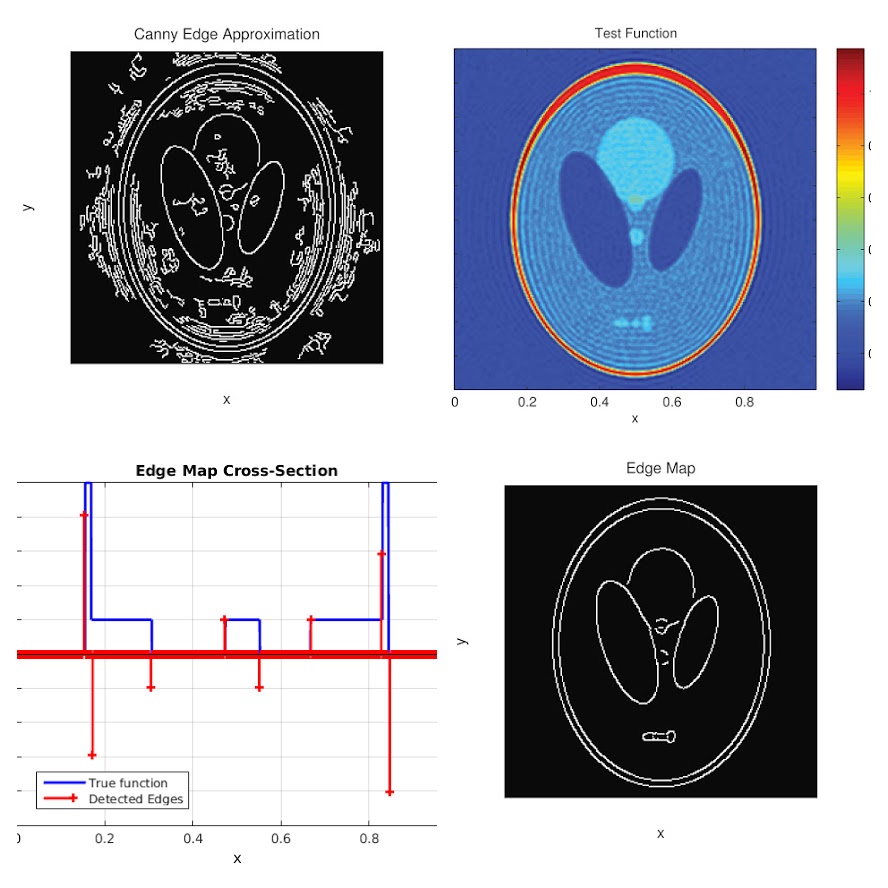
- efficient and accurate methods of identifying edge information from Fourier data, and
- use of this edge information in constructing augmented Fourier approximations with improved convergence rates and reduced Gibbs artifacts.
I have previously worked on the non-harmonic Fourier reconstruction problem, including use of spectral reprojection methods to mitigate the ill-effects of non-harmonic sampling and Gibbs artifacts, as well as edge detection from Fourier data using the concetration kernel method (which uses specially chosen “filter” factors and Fourier partial sums to approximate jump locations and heights).
Related Material:
- Edge-augmented Fourier reconstructions [preprint]
- Design of concentration kernels for edge detection from Fourier data [preprint]
- Some slides summarizing the main results
- Matlab code implementing edge-augmented Fourier reconstruction [FourierRecon]
Collaborators: Anne Gelb (Dartmouth), Doug Cochran (Arizona State University), Rosemary Renaut (Arizona State University), Mark Iwen (Michigan State University).
Numerical Methods for PDEs
I am interested in efficient (linear-time), unconditionally stable, spatially and temporally high-order accurate algorithms for solving computational wave propagation problems in challenging (general curvilinear, embedded boundary, multi-mesh) geometries. Of particular interest are computational electromagnetics problems such as the design and simulation of photonic waveguides and oscillators, wave scattering in complicated geometries, as well as biomedical applications such as high-frequency focused ultrasound. I currently work on the design of non-reflecting boundary terminations for a special class of unconditionally stable 𝒪(N)-time Method of Lines Transpose-based wave propagators.
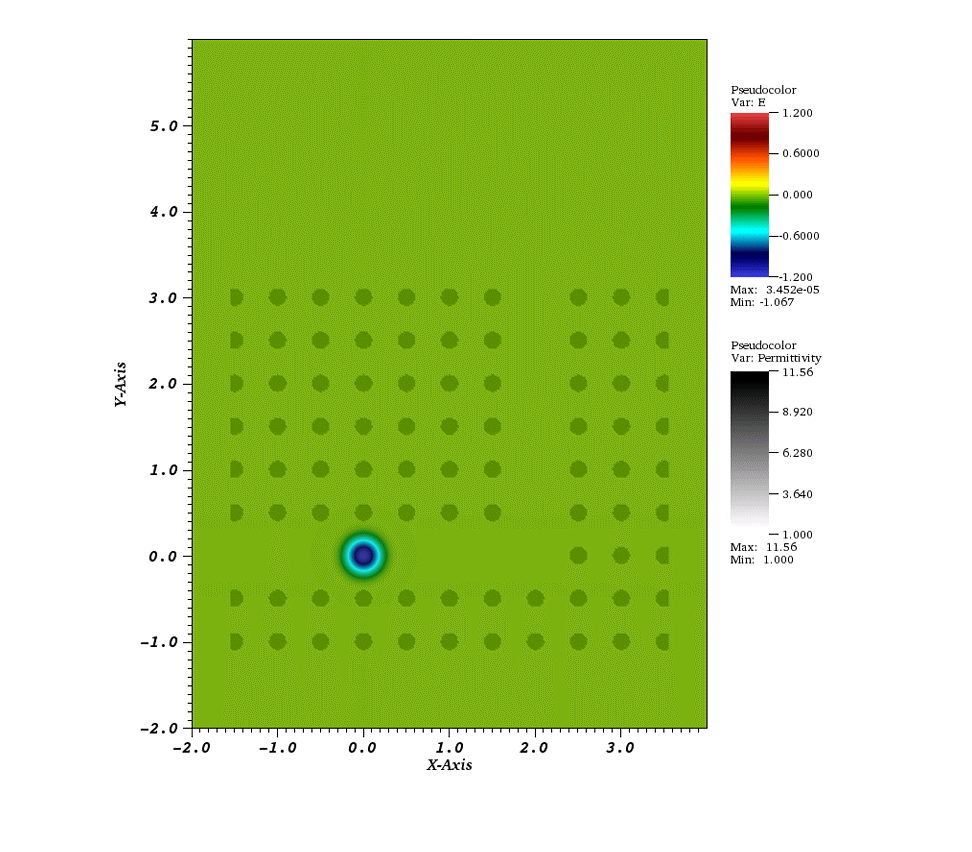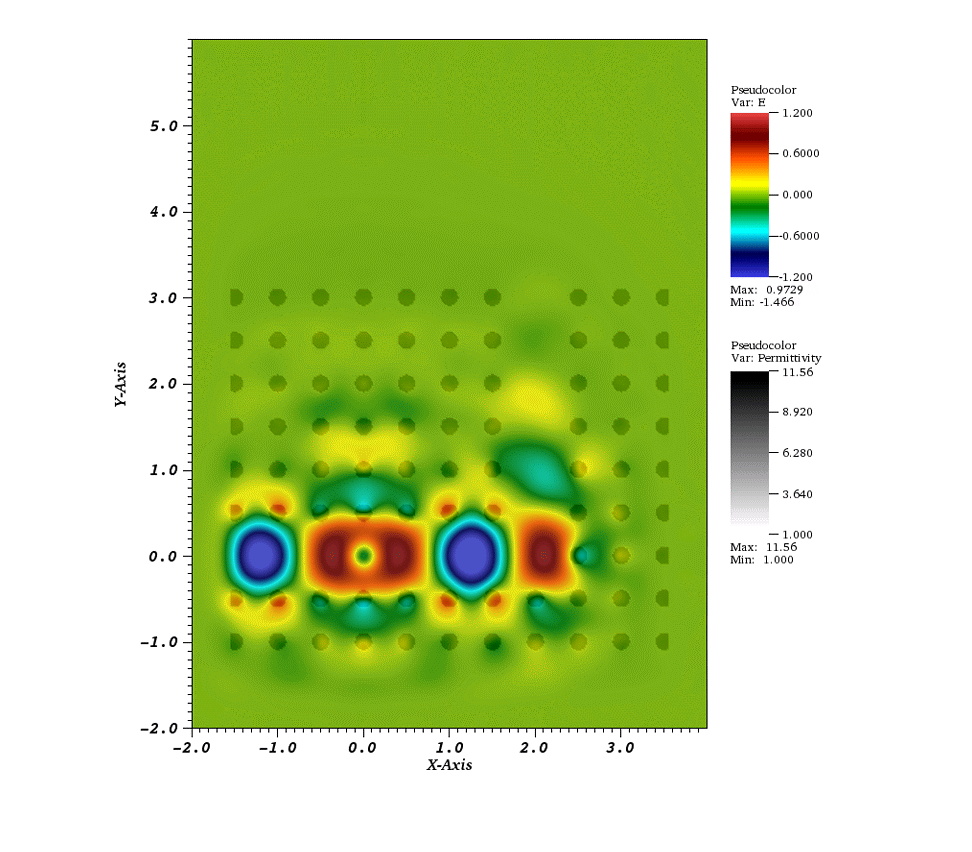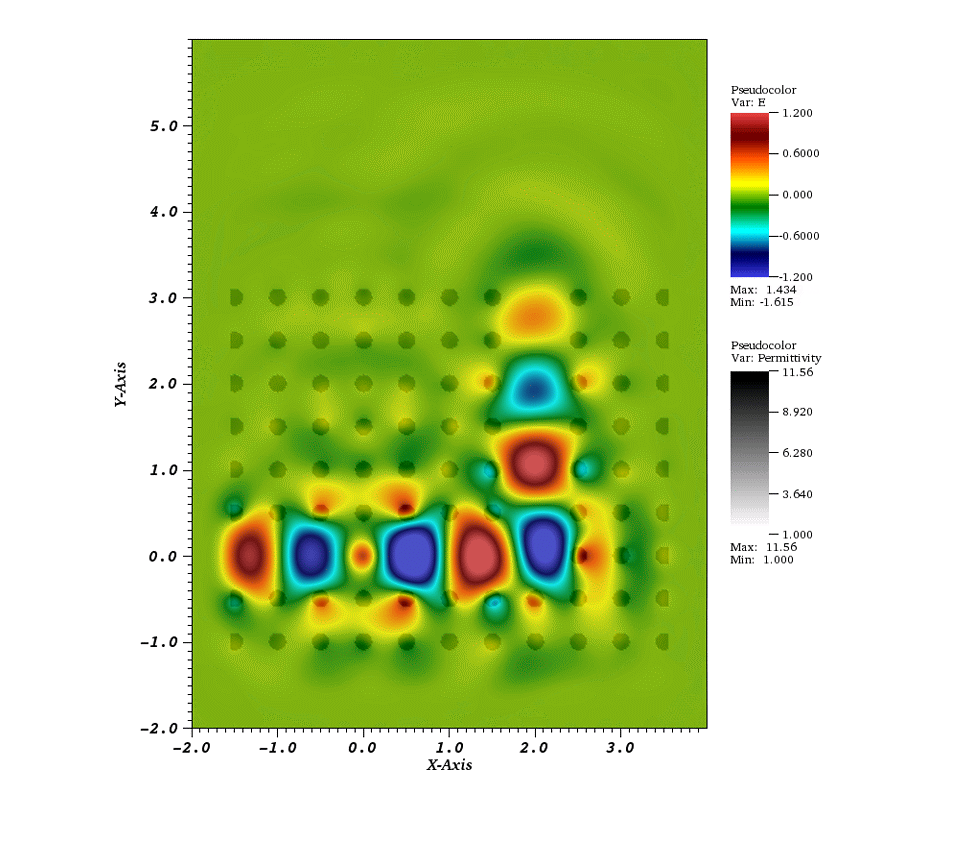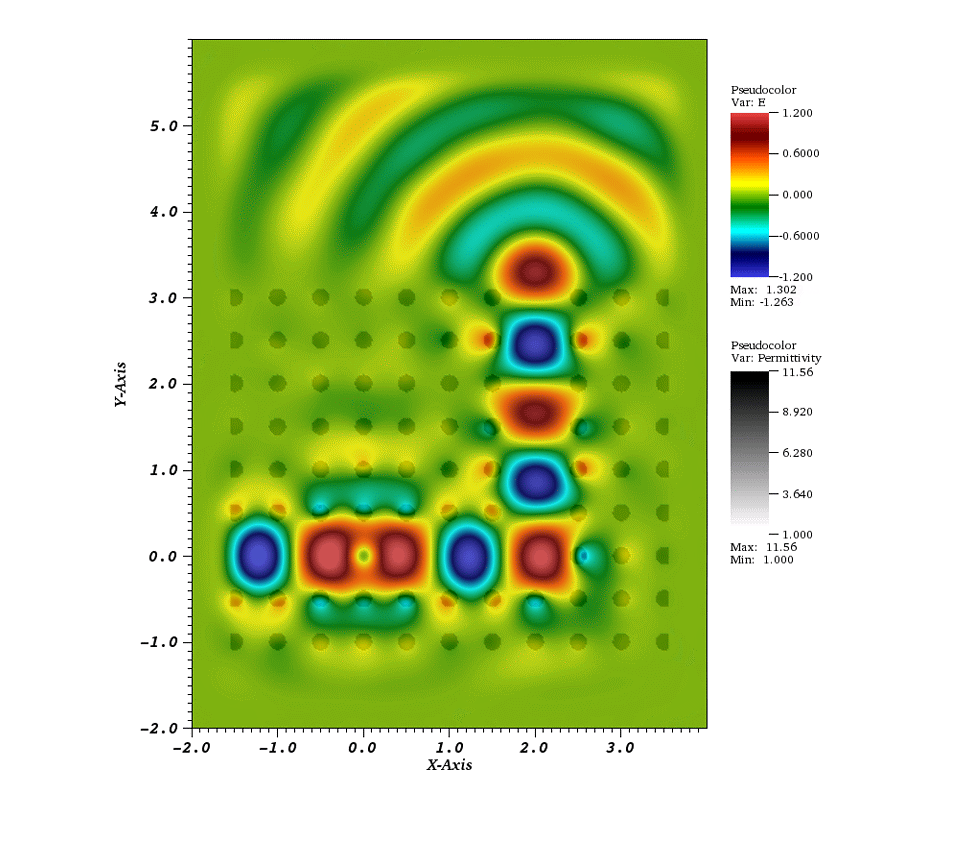
Previously, I have worked on (with Oscar Bruno, Edwin Jimenez, Caltech) Fourier Continuation (FC)-based wave propagation solvers in two- and three-dimensional general curvilinear domains. FC-based spatial approximations enable the realization of high-order, essentially dispersionless and spectral-like solvers on an equispaced mesh while imposing relatively mild CFL constraints. I was also part of a multi-disciplinary research effort developing next-generation drug delivery schemes for the treatment of tumors. The project involved modeling the evolution of magnetic nano-particle coated drugs under the influence of diffusion processes and external magnetic fields.

Collaborators: Oscar Bruno (Caltech), Edwin Jimenez (Caltech), Andrew Christlieb (Michigan State University).