Conjugate Filter OscillationReduction (CFOR) scheme for the 2D Richtmyer-Meshkov instability
Richtmyer-Meshkovinstability (RMI) refers to the instability occurs at an impulsively acceleratedinterface between two different gases. It differs from theRayleigh-Taylor instability for which the acceleration at the interface is aconstant, and from the Kelvin-Helmholtz instability which is due tothe shear stress between the two fluids at the interface. Richtmyer-Meshkovinstability is abundant and omnipresent in nature as well as technologicalapplications. The study of Richtmyer-Meshkov instability is of particularimportance to a large number of science and engineering applications, such asnuclear explosions, inertial confinement fusion (ICF) capsule implosions,supernova explosions, supersonic and hypersonic combustion in air breathingvehicles, flows in shock tubes, laser-matter interaction, to name only a few.
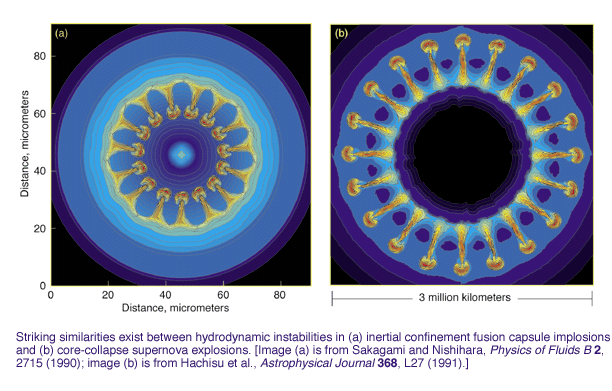
Numerical simulations are indispensable tools for estimating how the growthrate of the instability depends on a number of physical parameters, suchas the Mach number of the incident shock, the density difference of two gasfluids, the compressibility of the two fluids, the size, shape and initialperturbation of the interface. Accurate simulation of Richtmyer-Meshkovinstability is notoriously challenging. What is involved is theinteraction of shock and turbulence. It requires both high (spectral)resolution and ability of efficient shock capturing.
Conjugate filter oscillationreduction (CFOR) scheme is constructed by using a
Some facts about theCFOR scheme that can be found in a JCP paper:
(1) A factor of 1,000,000 times more accurate than the standard 4th orderfinite difference scheme for wave propagations.
(2) Unparallel reliability in long time integration. The error (L1 or L2)at t=100 is about 1/10,000,000 for the propagation of a 2D isentropic vortexgoverned by the Euler's equations.
(3) Less than 3 points per wavelength (PPW) to resolve compressibleor incompressible waves governed by the Navier-Stokes or Euler'sequations.
(4) Just 5 PPW to fully resolve the interaction of shock and oscillatoryentropy waves governed by Euler's equations.
Preliminary results
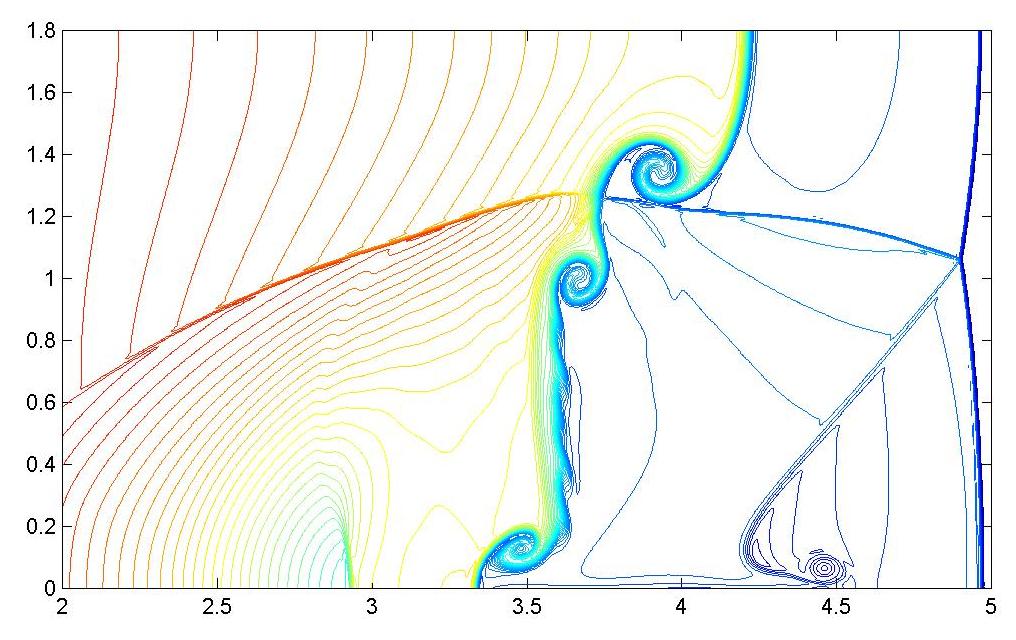
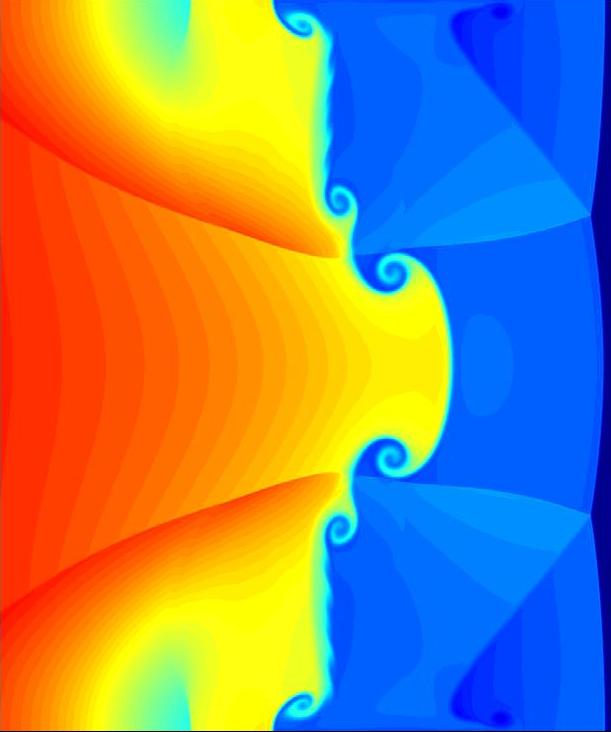
Mach number 4.46, domain 5x1.8 cm^2, resolution 1024x512, time 5.0e-5second
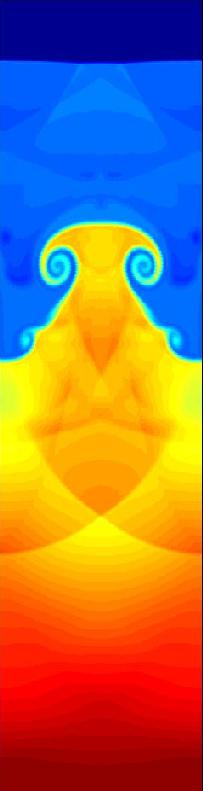
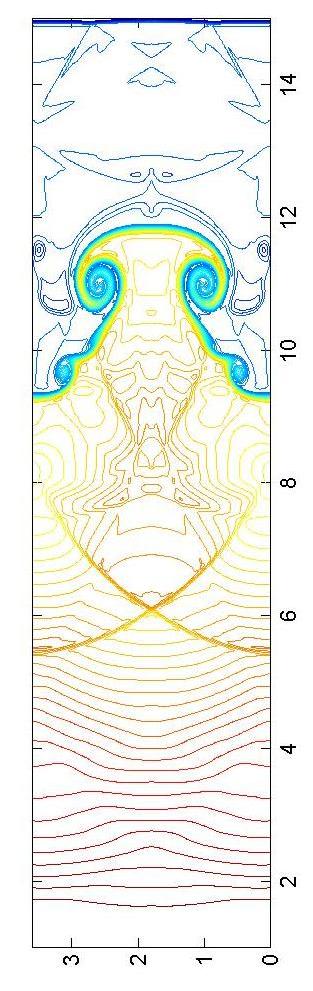
Mach number 4.46, domain 15x3.6 cm^2, resolution 768x256, time 1.4e-4 second

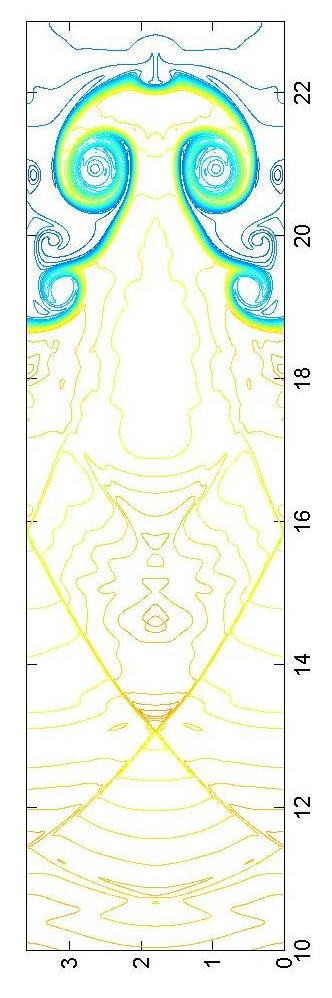
Mack 10, t=1.2e-4
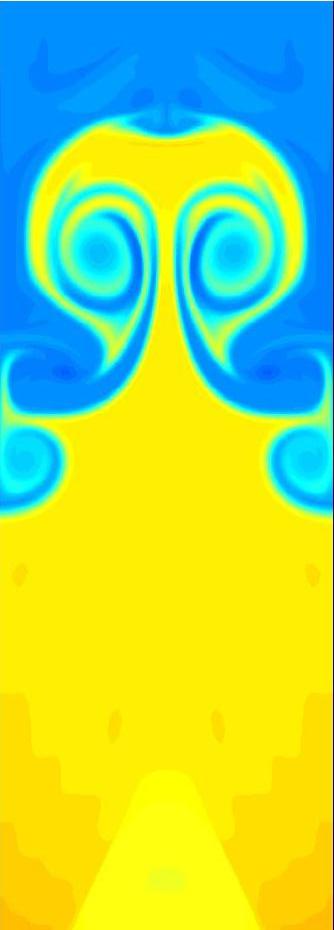

Mack 10, t=2.16e-4
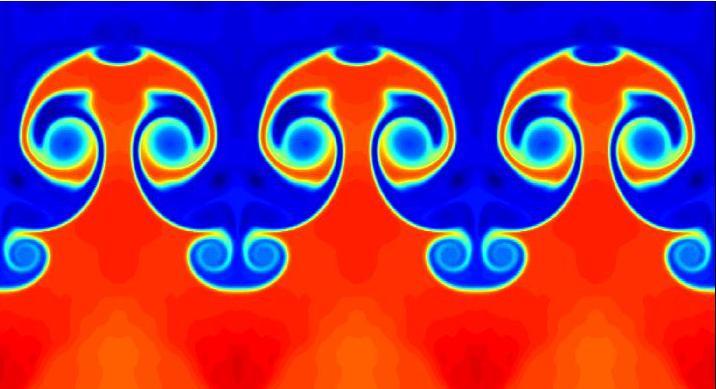
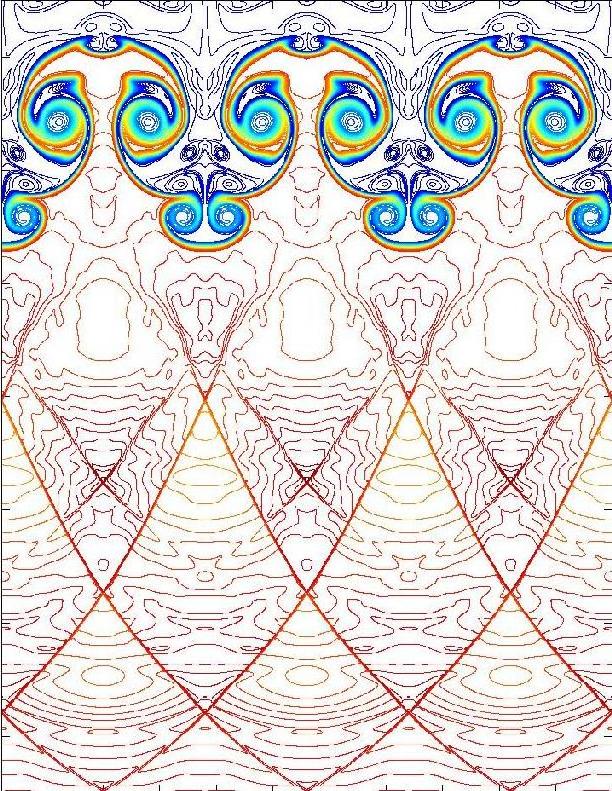
Mack 20, t=6.5e-5
Reference:
G.W. Wei, and Yun Gu, Conjugated filter approachfor solving Burger's equation, J. Comput. Appl. Math., 149, 439-456 (2002).
Yun Gu and G.W. Wei, Conjugated filter approachfor shock capturing, Commun. Numer. Meth. Engng. , 19, 99-110(2003).
Y.C. Zhou, Yun Gu and G.W. Wei, Shock-capturing withnatural high frequency oscillations, Int. J. Numer. Methods inFluid, 41, 1319-1338 (2003).
Y.C. Zhou and G.W. Wei, High-resolution conjugatefilters for the simulation of flows, J. Comput. Phys., 189,150-179 (2003).
Links: