Controlling Chaos
Wavelets andassociated multiresolution analysis have had tremendous impact on signal/imageprocessing, data compression, computer vision, telecommunication and a varietyof other engineering disciplines. Recently, their applications can be seen inmany areas of science, such as the analyses of time series, low-dimensionaldynamics, turbulence cascades, spatial hierarchies in measles epidemics,
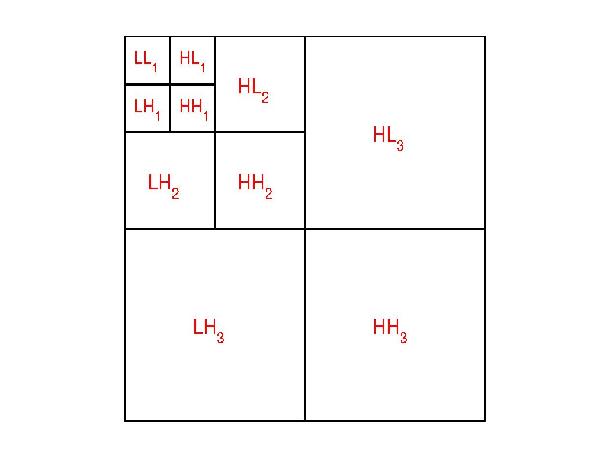
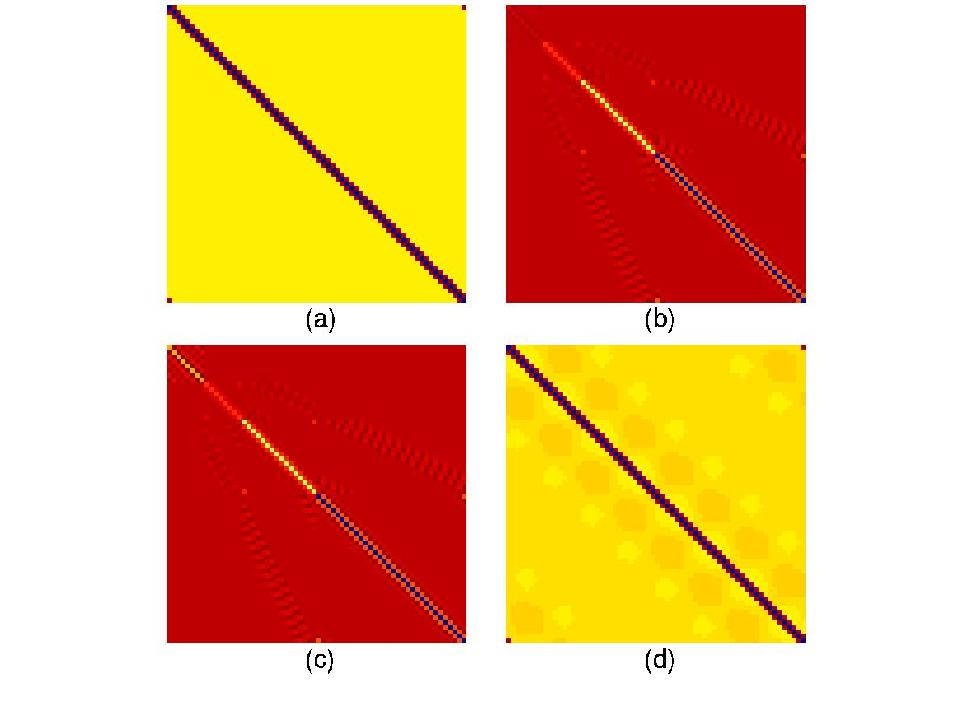
The impact of wavelet subspace control ofa coupling matrix. (a) Original coupling matrix; (b) Wavelet representation of the coupling matrix; (c) Wavelet representationof the modified coupling matrix; (d) Physical spaceimage of the modified coupling matrix.
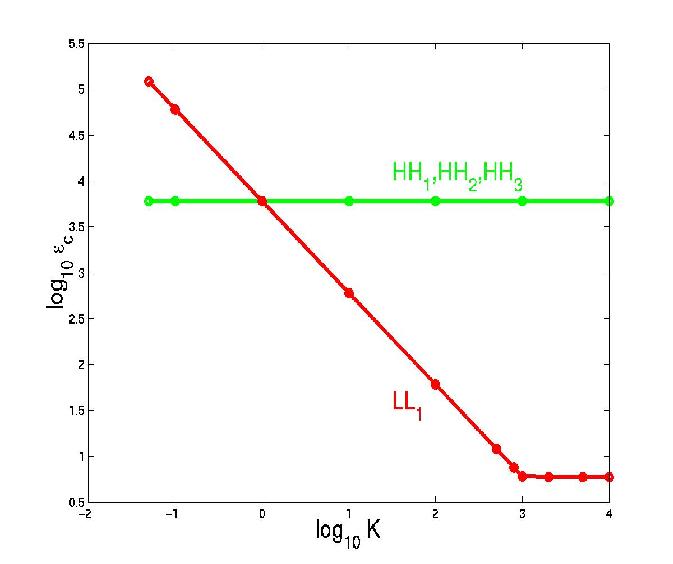
Reduction in critical coupling strengthafter wavelet subspace control based on the coupled Lorentz system.
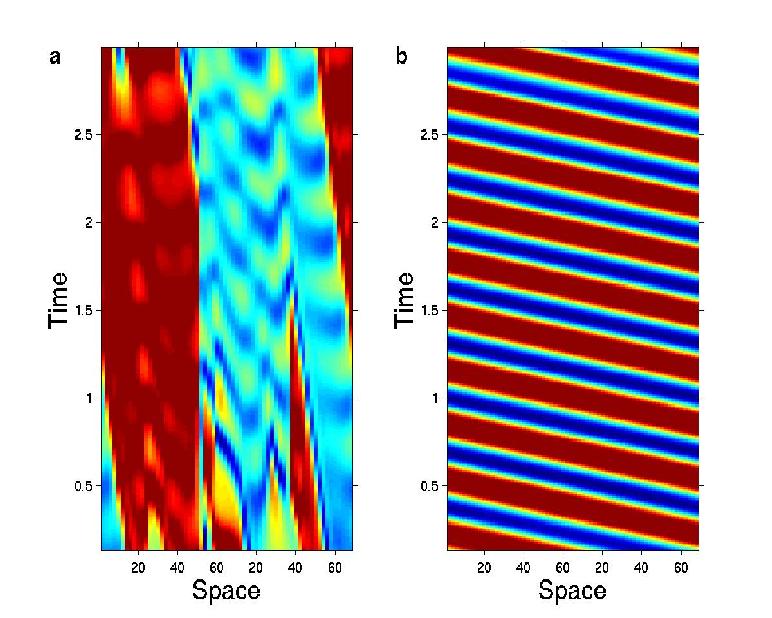
Wavelet induced Hopf bifurcation fromchaos in the coupled Lorentz system.
Reference:
G.W. Wei, M. Zhan, and C.-H. Lai, Tailoringwavelets for chaos control, Phys. Rev. Lett. 89, 284103(2002). This work was highlighted in