MTH 235

Lab 02: Harmonic Oscillators, Forcing, Damping, and Resonance

• Introduction
• Undamped Oscillations
• Resonance in Undamped Oscillations
• Damped Oscillations
• Resonance in Damped Oscillations
• Example: The Collapse of the Tacoma Narrows Bridge

Introduction

The study of vibrations, which can occur in various engineering structures, is an important part of making sure the design of the structures (buildings, bridges, etc.) is sound. Many modern designs incorporate damping, which serves to remove energy from the physical system and thus mitigates potentially catastrophic events such as resonance or near-resonance of the system. In this lab we will study a mass-spring system, which despite the fact that it is much simpler than a bridge or a building, can still help us understand the phenomenon of resonance and damping effects.

Undamped Oscillations

A mass-spring system is a mass \(m\), attached to a spring with spring constant \(k\), that slides on a frictionless table. We denote by \(y(t)\) the displacement of the mass as a function of time, where \(y = 0\) represents the rest position of the mass.

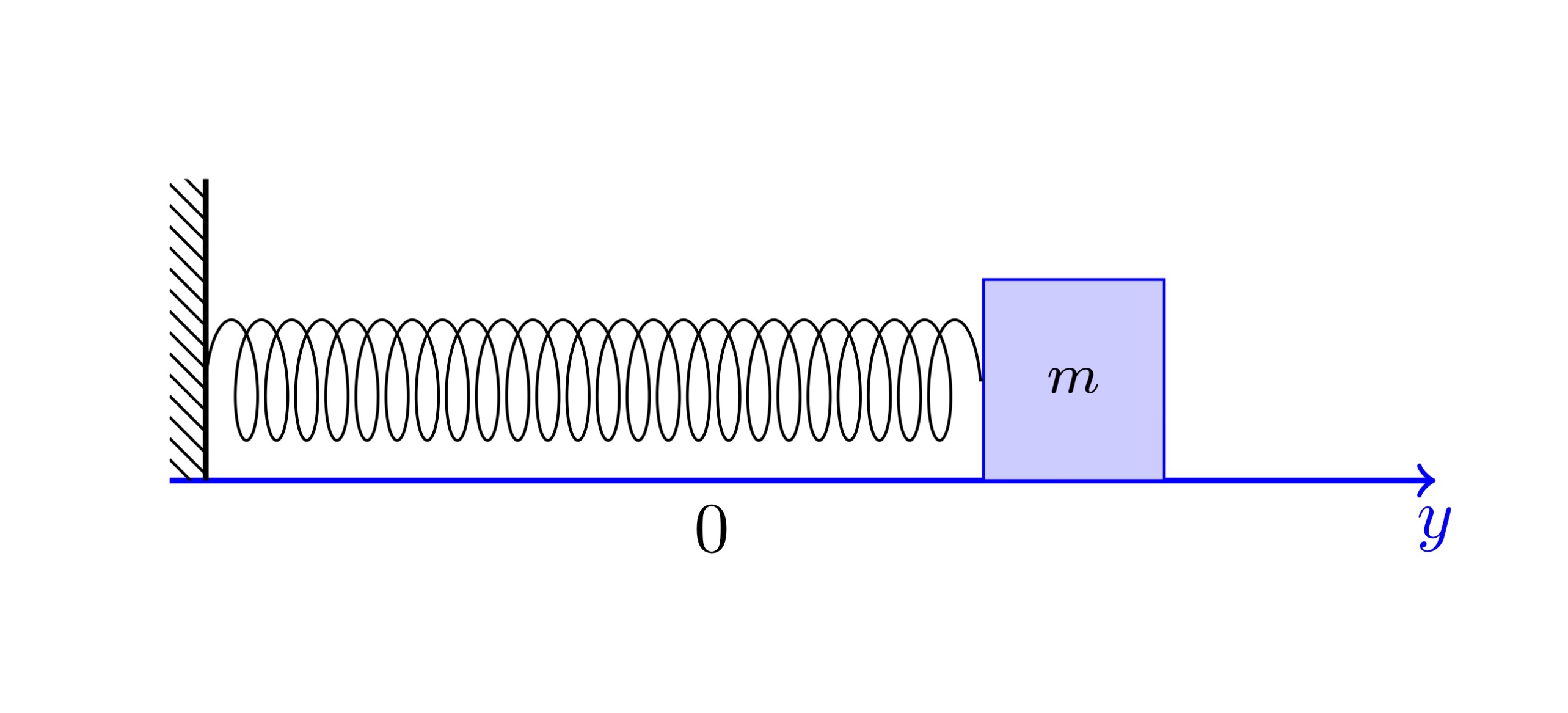
This system is described by Newton's law of motion \(ma=f\), where \(a(t) = y''(t)\) is the body acceleration and \(f\) is the sum of all forces acting on the body. In this case the only force is Hooke's law, which says that the force exerted by the spring is \(f = - ky\), where \(k>0\) is a constant that determines the stiffness of the spring. Therefore, the position function, \(y\), of the body attached to the spring is the solution of the differential equation \[ \tag{1} m\, y''(t) = - k \, y(t). \] The equation above is often referred to as the differential equation of an undamped oscillator. Recall that the general solution to Eq. (1) is given by \[ \tag{1} y(t) = A \cos(\omega t -\phi), \] where \(\omega\) is the natural frequency of the system, \(A\geqslant 0\) is the amplitude and \(\phi \in [-\pi,\pi)\) is the phase shift of the solution.

Problem 1:

1. Find a formula for the natural frequency (as a function of the mass and the spring constant).
• How does the frequency change when you change the spring constant \(k\). Does the effect you observe on the graph agree with the formula you found above?
• Interactive Graph 1: Understanding Amplitude and Phase Shift.
2. The amplitude \(A\) and phase shift \(\phi\) of the solution can be determined in terms of the initial position \(y(0) = y_0 \) and initial velocity \(y'(0) = v_0 \). The result is, \[ A= \sqrt{y_0^2 + \dfrac{v_0^2}{\omega^2 y_{0}^2}}, \qquad \phi = \arctan\Bigl(\frac{v_0}{y_0\omega}\Bigr). \]
3. Answer the following questions:
• How do the initial conditions affect the natural frequency? What happens to the frequency if \(y_0\) and \(v_0\) are large vs. when they are small?
• How do the initial conditions affect the amplitude? What happens to the frequency if \(y_0\) and \(v_0\) are large vs. when they are small?
• Interactive Graph 2: Understanding the Effect of the Initial Conditions.
4. In your group discuss if these observations make physical sense, i.e. could you have predicted them without looking at the graphs?

Resonance in Undamped Oscillations

• No Resonance (\( \nu \neq \omega\) ): Consider a similar set-up to the undamped harmonic oscillator described above, but now add an external sinusoidal force of the form \( F_e(t) = m\nu\cos(\nu t)\), where \(\nu>0\) is the angular driving frequency. We first study the case \(\nu \neq \omega\), where \(\omega\) is the system natural frequency. In this case, Newton's equation of motion is \[ \tag{2} y''(t) + \omega^2 \, y(t) = \nu \cos(\nu t), \qquad \nu \neq \omega. \] A particular solution, \(y_p\), of Eq. (2) can be found using either the Undetermined Coefficients or the Variation of Parameters method, and it is given by \[ \tag{3a} y_p(t) = \frac{\nu}{(\omega^2-\nu^2)}\cos(\nu t). \] One can show that the only solution satisfying the initial conditions \(y(0)=0\) and \(y'(0) =0\) is \[ \tag{3b} y(t) = \frac{\nu}{\omega^2-\nu^2} \,\bigl( \cos(\nu t) - \cos(\omega t)\bigr). \]
• Resonance (\(\nu = \omega\)): We now consider the case where the external sinusoidal force of the form \( F_e(t) = m\omega\cos(\omega t)\), where \(\omega\) is the natural frequency of the system. Newton's equation of motion is \[ \tag{4} y''(t) + \omega^2 \, y(t) = \omega \cos(\omega t). \] A particular solution, \(y_p\), of Eq. (4) can be found using either the Undetermined Coefficients or the Variation of Parameters method, and it is given by \[ \tag{5} y_p(t) = \frac{t}{2}\sin(\omega t). \] The solution in (5) is the only solution satisfying the initial conditions \(y(0)=0\) and \(y'(0) =0\).

Problem 2:

1. Using Eqs. (3b)-(5), describe the behavior of this system near resonance, i.e., what happens to the amplitude as \(\nu\to\omega_0\)?
2. Use the interactive graph to observe and describe the phenomenon of beating.
• Interactive Graph 3: Resonance for Undamped Oscillation.
• Interactive Graph 4: Understanding Beating.

Damped Oscillations

Consider a mass-spring system with mass \(m\), attached to a spring with spring constant \(k\), that slides on a table. As before, we denote by \(y(t)\) the displacement of the mass as a function of time, where \(y = 0\) represents the rest position of the mass. Assume there is a friction force between the object and the table, proportional to the object velocity and acting in the opposite direction, that is \( f_d = - d\, y'\), where \(d>0\) is the damping constant. Newton's equation of motion in this case is \[ \tag{6} m\, y''(t) = -k \, y(t) - d\, y'(t) \quad\Longrightarrow\quad y'' + 2 \omega_d \, y' + \omega^2 \, y =0, \] where \(\omega_d = \dfrac{d}{2m}\) is the damping frequency. Recall that the general solution to Eq.(6) is given by \[ \tag{7} y(t) = A \, e^{\alpha t} \cos(\beta t -\phi), \] where \(A>0\) is the amplitude and \(\phi\in [-\pi, \pi)\) is the phase shift.

Problem 3:

1. Find the decay constant, \(\alpha < 0\), as a function of the parameters of the system. Before deriving the analytical expression, discuss in your group whether it should depend on the mass, the spring stiffness, or on the damping. Does the formula you derived agree with your physical intuition?
2. What can we conclude about the long-term behavior of the solution of an unforced harmonic oscillator with damping? (That is, \( \displaystyle\lim_{t\to\infty}y(t)=?\) ) Does this make sense from a physical point of view?
3. Does the long-term behavior of \(y(t)\) in this case depend on the initial conditions? Explain.
4. Interactive Graph 5: Solutions with Damping.

Resonance for Damped Oscillations

• Consider a similar set-up to the damped harmonic oscillator described above, but now add an external sinusoidal force of the form \( f_e(t) = m\nu\cos(\nu t)\), where \(\nu>0\) is the angular driving frequency. Newton's equation of motion is \[ \tag{8} m\, y''(t) = -k \, y(t) - d\, y'(t) + m\nu \cos(\nu t) \quad\Longrightarrow\quad y'' + \omega_d \,y' +\omega^2\,y = \nu\cos(\nu t), \] where \(\omega_d = \dfrac{d}{2m}\) is the damping frequency.
• Near Resonance (\(\nu\sim\omega\)) and Resonance (\(\nu=\omega\)): We now consider the case where the external sinusoidal force satisfies that \(\nu = \omega\). A particular solution, \(y_p\), of Eq. (8) can be found using either the Undetermined Coefficients or the Variation of Parameters method, and it is given by \[ \tag{9} y_p(t) = A_p\, \cos(\nu t-\phi_p), \] where amplitude \(A_p\), the phase shift \(\phi_p\), are given by \[ \tag{10} A_p = \frac{\nu}{\sqrt{(\omega^2-\nu^2)^2 + 4\omega_d^2\nu^2}}, \qquad \phi_p = \arctan\Bigl(\frac{2\omega_d\nu}{(\omega^2-\nu^2)} \Bigr). \] Notice that the amplitude is finite for \(\nu=\omega\).
• One can show that the only solution satisfying the initial conditions \(y(0)=0\) and \(y'(0) =0\) is \[ \tag{11} y(t) = \bigl(c_1 \cos(\beta t) + c_2 \sin(\beta t) \bigr) \, e^{-\omega_d t} + A_p \cos(\nu t-\phi_p), \] where the constants \(c_1\), \(c_2\), and the frequency \(\beta\) are given by \[ c_1 = - A_p\cos(\phi_p), \qquad c_2 = -A_p \Bigl( \frac{\omega_d}{\beta} \cos(\phi_p) + \frac{\nu}{\beta}\sin(\phi_p) \Bigr), \qquad \beta = \sqrt{\omega^2-\nu^2}. \]

Problem 4:

1. Use the interactive graph to describe the behavior of this system near resonance.
2. How does the damping coefficient, \(d\), affect the solution?
3. Does damping help with near-resonance effects, i.e. is the amplitude of the oscillations reduced due to damping? What if \(d\) is very small and the forced frequency is very close to the natural frequency?
4. Interactive Graph 6: Amplitude as Function of the Driving Frequency (\(A_p(\nu)\)) in the Particular Solution \(y_p\) in Eq.(10): .
5. Interactive Graph 7: Plot of the Particular Solution \(y_p(t)\) in Eq.(9).
6. Interactive Graph 8: Solution \(y(t)\) of the IVP in Eq.(11) with Damping and Including Resonance.

Example: The Collapse of the Tacoma Narrows Bridge

Perhaps one of the most known examples of resonance is the break of the Tacoma bridge in 1940.