5.8 Friedrichs Extension and Galerkin Approximations
Theorem 2.12.6 showed that an elementary to verify algebraic condition implies convergence of Galerkin approximations to the solution of an elliptic problem, where the elliptic operator is the Friedrichs extension determined by the basis functions. The same holds for parabolic and wave type equations. In the case of parabolic equations we have: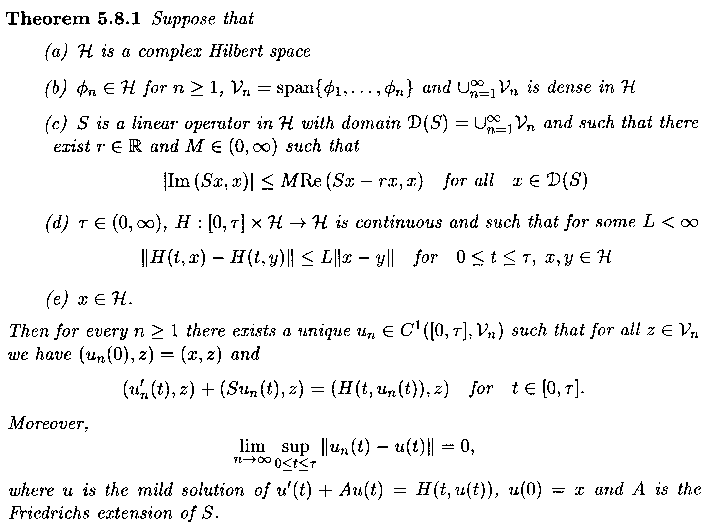
PROOF Theorem 2.12.1 implies that all assumptions of Section 5.6 are satisfied. Hence, the assertions of the Theorem follow from Theorem 5.6.1.
