MSU Math Home | Mathematics Research| Colloquium, Fall 1997| Colloquium, Spring 1998

Counting Rational Curves on Projective Varieties


Aaron Bertram,
University of Utah

Even in the case of the complex projective plane, the result is stunning. Let Nd denote the number of rational curves of degree d passing through 3d-1 general points in ${\bf CP}^2$. Then the ``potential function'':

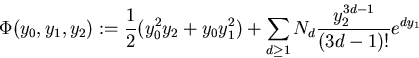
\begin{displaymath} \Phi(y_0,y_1,y_2) := \frac 12(y_0^2y_2 + y_0y_1^2) + \sum_{d \ge 1} N_d \frac{y_2^{3d-1}}{(3d-1)!} e^{dy_1}\end{displaymath}

satisfies the following partial differential equation:

\begin{displaymath} \Phi_{222} = \Phi_{112}^2 - \Phi_{111}\Phi_{122}\end{displaymath}

which determines a recursive formula for the Nd.


Such a statement, unimagined in the course of more than a hundred years of study of such numbers by enumerative algebraic geometers, is a typical result coming from the theory of quantum cohomology. In this talk, I will explain how the rational curves on a smooth projective variety determine a potential function and system of 3rd order partial differential equations in general. I'll explain why there is a commutative ring hiding here, and talk about some interesting examples.