Office hours: Mon, Wed, Fri 10:30-1, and Thu afternoon by appointment.
- Welcome to Math 481. This page will have all assignments and notes. Check here frequently for homework updates and corrections.
First lecture: Mon 1/11 at 9:10 in Wells A-328.
(Room assignment recently changed.)
- Homework before first lecture: Quiz 1 (on 1/11) will cover the following problem. Given two people chosen at random, what is the probability that they have the same birthday? Assume 365 equally likely days in a year, and ignore leap years.
- Reading HW Solutions: To see the HW solutions one at a time, open a new browser window and size it so that it shows only one problem, like this. You can achieve the same effect by folding a printout.
- Final Exam Study:
- The Exam will be Tue May 3, 7:45−9:45am in our usual classroom, Wells A-328.
- The test will cover the whole course about equally. The problems will be similar to the Quizzes, though sometimes more involved. Study as for the Midterm.
- Re-do all quizzes before looking at your previous answers and my answers from class notes. Make sure you understand all mistakes. I can email you any missing quizzes on request.
- Do Review HW posted below, including the Review Supplements. (Don't just read the solutions!)
- Review old notes, class notes, and the HHM text.
- Make study cards to memorize the details of:
- Basic Principles: Sum, Product, Difference (PIE), Quotient (Burnside's Formula), Transformation
- 4 Basic Problems: n!, nk, (n|k), ((n|k)).
- Binomial Theorem and the Known Power Series
- Euler's Formula, Edge-Vertex Formula, Edge-Region Inequality, and how these specialize to regular or polyhedral graphs.
- Review old homework, and finish problems you didn't do.
- Extra Credit: I will accept Extra Credit problems
from any HW, and also revised Proof HW
(together with the old version),
until class time on Fri Apr 29.
I will not collect homework (except problems marked Hand In), but the next daily quiz will be based on it. You may also hand in problems marked Extra Credit, preferably within a week of the HW date. Each problem you give up on is a lost opportunity to learn: only look at the solution after a serious effort.
I will give 1 extra point to the first person pointing out a significant typo or other error on this page. Corrections and recent revisions are in red. Future assignments, which are tentative and may be revised, are marked in gray.
On this page, I will denote the binomial coefficient (n choose k) as (n | k), and the multi-set number (n multi-choose k) as ((n | k)). Use the standard vertical notation on your papers.
HW:
- There are six students in a class. Use the Product Principle to solve the following enumeration problems.
- How many ways for the students to line up? If they all line up at random, what is the chance the line is in alphabetical order?
- How many ways to choose a class president, vice-president, and secretary (with no one holding two positions)?
- Write each counting problem above in set notation. That is, define the set of cases A, so that the answer is |A|.
- The four-digit numbers are: 1000, 1001, 1002, …, 9999.
- How many four-digit numbers are there? Justify your answer using the Product Principle.
- How many have all four digits different? Example: 1234 or 5203, but not 5202. Justify your answer using the Product Principle.
- If you choose a random four-digit number, what is the percentage probability that all four digits are different?
- A fair coin is tossed 10 times.
- What is the chance of 10 heads in a row?
- What is the chance of at most one tail?
- What is the chance of at least two tails?
- Set notation. Given any sets A,B, we define:
- The union A∪B, the set of elements which are in A or in B (or both).
- The intersection A∩B, the set of elements which are in A and in B.
- The set difference A\B, the set of elements which are in A but not in B.
- The cartesian product A×B, the set of pairs (a,b), where a∈A and b∈B.
- The subset relation A ⊂ B, meaning A is contained in B, i.e. every element of A is also an element of B.
- Write out all elements in A∪B, A∩B, A\B, and A×B.
- Write out all subsets of A, of B, and of A×B. How many are there in each case?
- Use set-notation to define the set of triples T, whose elements are all lists of 3 elements of A. For example, (a,b,a) ∈ T.
- We often write 3-dimensional space as R3, where R is the set of real numbers. Explain this notation: how does it relate to Cartesian product of sets?
- Is it ever true that S ⊂ S×T, for some sets S,T?
- Extra Credit: In class, we found that the probability of k people having a coincidence of birthdays is: 1 − 365k / 365k , assuming 365 days in a year.
- Do the k = 4 version of this problem by positive counting (splitting into cases). Make sure you do not miss any cases, and check your answer numerically against the above formula.
- Redo this problem for general k, but taking leap-years into account. Hint: The answer is not 1 − 365.25k / 365.25k. Instead, take as your probability space all the days in a four-year period, in which the leap-day Feb 29 occurs once.
- Find the probability for at least two distinct pairs of coincident birthdays (as we got in class); also for a triple coincidence. Explore this topic.
1b. This is a list of 3 students from the 6, with no repeats. We can choose the president to be any of the 6, the vice-president from the remaining 5, etc., so the number of possibilities is 63 = 6×5×4 =120.
1c. Let S be the set of 6 students. For the first problem, let A = { (a,b,c,d,e,f) s.t. {a,b,c,d,e,f} = S }; that is, the set whose elements are lists (a,b,c,d,e,f) which, when considered as sets {a,b,c,d,e,f}, make the full set of students. For the second problem, let A = { (a,b,c) s.t. a,b,c ∈ S and a≠b, a≠c, b≠c }; that is, the set whose elements are triples of distinct elements of S.
2a. The first digit can be 1,...,9, the rest can be 0,1,...,9, so there are 9×10×10×10 = 9000.
2b. The first digit can be 1,...,9, the second can be 0,1,...,9 but different from the first digit, etc., so there are 9×9×8×7 = 4536.
2c. 4536/9000, a bit over 50%.
3a. A result is a list of 10 heads or tails, so the possibilities are 210 = 1024. There is only one way to get all heads, so the probability is 1/1024.
3b. There is 1 way to get no tails and 10 ways to get exactly one tail, so the probability is 11/1024, about 1%.
3c. This is the complement of 3(b), all lists of 10 tosses which do not contain at most one tail. Thus the probability of this case is: (1024−11) / 1024 = 1 − 11/1024 .
4a. We have A∪B = {a,b,c}, A∩B = {b}, A\B = {a}, A×B = {(a,b), (a,c), (b,b), (b,c)}
4b. A has 4 subsets {a,b}, {a}, {b}, {}. B has 4 subsets {b,c}, {b}, {c}, {}. The set A×B has 16 subsets, for example {(a,b), (b,b), (b,c)}. Can you find a general rule predicting how many subsets a set will have?
4c. T = A3 = A×A×A.
4d. R3 = R×R×R = {(x,y,z) s.t. x,y,z ∈ R}, the set of possible coordinates for the points of space.
4e. Usually, no. S×T is a set whose elements are pairs (s,t), so no element s∈S can be an element of S×T. However, if S = {}, the nullset with no elements, then S×T = {} also has no elements, and S ⊂ S×T. Also, we might manage it for some weird sets of inifinite lists.
HW:
- A class has 20 students.
- How many ways to choose a basketball team of 5 from the 20 students? (There is no order among team-members.)
- How many ways to choose two teams of 5 (an A team and a B team)?
- How many four-digit numbers have distinct, increasing digits? Example: 1234 or 4679, but not 4659.
- In a standard deck of 52 cards, each card has one of 13 face values (A,2,3,...,J,Q,K) and one of 4 suits (♠,♣,♥,♦). A hand is an unordered set of 5 distinct cards. Compute the number of ways of dealing the following hands, and the corresponding probability.
- One pair: two cards with a common face value and another three with all different face values. Ex: {7♥, 7♠ 2♣, 10♣, K♦}
Hint: First choose the face values of the cards, then the suits. - Two pairs: two cards with a common face value, another two with a different common face value, and one extra card with a third face value.
- Full house: three cards with a common face value, another two with a different common face value.
Hint: There is a subtle difference between this hand and two pairs. - Straight: all face values in sequence (A,2,3,4,5; or 2,3,4,5,6; or ... or 10,J,Q,K,A), but not all of the same suit (which would make a straight flush).
- Extra Credit: Give a brief but clear combinatorial analysis of each type hand in poker, and show that the ranking of their value corresponds to decreasing probability of each type (high-card the most likely, then one pair, all the way to straight flush the least likely).
- One pair: two cards with a common face value and another three with all different face values. Ex: {7♥, 7♠ 2♣, 10♣, K♦}
- In a grid of city streets, you want to walk to a store 5 blocks north and 10 blocks east. At each corner you must choose whether to walk north or east. How many possible routes?
- You have 5 red balls and 3 black balls, which you lay out in a row.
- How many different arrangements are possible? Example: • • • • • • • •
- How many arrangments with no two black balls next to each other? Example: • • • • • • • •
1a. Basic Problem 3: Choose a set of 5 out of 20. Ans: (20 | 5) = 205 / 5! = 20×19×18×17×16 / 5×4×3×2 = 15504. Try computing a few of these on a calculator, then on a spreadsheet using the FACTORIAL and/or BINOMIAL functions.
1b. First choose 5 from 20, then 5 from the remaining 15. Ans: (20 | 5) (15 | 5) = 46558512.
2. A list of 4 increasing digits corresponds to a set of 4 digits chosen from {1,...,9}, since a set (without order) can always be written in increasing order. For example {2,3,5,9} corresponds to 2359. Ans: (9 | 4) = 94/4! = 126.
3a. A hand like {6♠, 6♥, 3♦, 8♠, J♥} corresponds to
the following choices: one face value (6) for the pair from the possible 13, and a set of 3 face values {3,8,J} from the remaining 12; then a set of two suits {♠,♥} for the pair from the 4 suits, and a list of suits (♥,♦,♠) for the 3 distinct face values.
Ans: 13 (4 | 2) (12 | 3) 43 = 1098240.
Note: The suits for the pair are interchangeable, which is why they form a set. Order matters for the suits of the other 3 cards, the suits for the lowest, middle, and highest face values: changing the order gives a different hand. Thus, these 3 suits form a list.
3b. A hand like {6♠, 6♥, J♦, J♥, 8♠} corresponds to
the following choices: a set of two face values {6,J} from the possible 13,
then another face value (8) from the remaining 11;
then a set of two suits {♠,♥} from 4 for the smaller pair and two suits {♦,♥} for the larger pair, and finally a suit ♠ for the last card.
Ans: (13 | 2) (13−2) (4 | 2) (4 | 2) 4 = 123552.
Note: The choice of face values for the two pairs is a set {6,J} = {J,6}, since 6,6,J,J is the same two pairs as J,J,6,6.
3c. Choose a face value for the triple, then a different one for the pair; then choose a set of 3 suits and a set of 2 suits.
Ans: 13 (13−1) (4 | 3) (4 | 2) = 3744.
Note: The choice of face values is a list like (6,J) ≠ (J,6), since 6,6,6,J,J is a different full house from J,J,J,6,6.
3d. Choose the low face-value of the straight: A or 2 or 3 or...or 10, then choose the 5 suits arbitrarily, but exclude all suits the same (4 cases). Ans: 10 (45 - 4) = 10200.
4. Of the 15 steps, choose which 5 are north (the other 10 must be east). Ans: (15 | 5) = 3003.
5a. Given a lineup of balls, record the positions of the black balls. The example • • • • • • • • corresponds to the set {3,5,6}, since there is a black ball in the 3rd, 5th, and 6th positions. This gives a 1-to-1 correspondence between the ball lineups and 3-element subsets of {1,2,...,8}. Ans: (8 | 3) = 56.
5b. Think of the 5 red balls as having 6 spaces between them (counting the two end spaces), and choose which 3 of these spaces is occupied by a black ball. Ans: (6 | 3) = 20.
- Notes 1/15: Multi-set numbers ((n | k)) and Position Transform.
- Ch 2.3 Multinomial coefficients, pp. 144-145 only.
- Make study flash-cards with the Basic Principles (+, −, ×, ÷, T) and Basic Problems 1,2,3,4.
- Position Transform. Find the probability of tossing either 3 or 4 heads out of 7 tosses of a coin (with heads or tails equally likely in each toss). Show how the objects to be counted correspond to certain sets, which are easy to count.
- Multinomial coefficients. A class has 20 students.
- How many ways to split the class into four teams of 5 each (teams A,B,C,D)?
- How many ways to choose just an A team and a B team from the class (with 5 each, no overlap)?
- Write each number above as a multinomial coefficient
(n | k1, k2, ... ),
the number of ways to split a set of n objects into
subsets of given sizes k1, k2,....
Verify that your answers above are equivalent to the general formula:
(n | k1, k2, ... ) = n! / k1! k2! ...
- Multi-choose numbers. How many ways to choose a basket of 10 fruits, which can be apples, bananas, oranges, or peaches? Example: 3 apples, 0 bananas, 5 oranges, 2 peaches, i.e. {A,A,A,O,O,O,O,O,P,P}. Write the result as a multi-set number ((n | k)), and compute it using the formula ((n | k)) = (n+k−1 | k) in the Notes below.
- How many four-digit numbers are there with increasing (but not necessarily distinct) digits? Example: 2556. Hint: Again use multi-set numbers.
- Distributing items among classes.
- How many solutions (a,b,c) are there to a+b+c = 10, assuming a,b,c are whole numbers ≥ 0? Example: (a,b,c) = (4,5,1) with 4+5+1 = 10. Hint: Multi-sets can be specified by how many of each kind there are.
- A soccer team consists of 11 members, with 1 goalie and the other 10 designated as defenders, midfielders, or forwards. How many configurations of a soccer team are there? Example: 1 goalie, 6 defenders, 0 midfielders, 4 forwards.
- How many soccer team configurations are there, if there must be 1 goalie and at least 2 players in each of the other positions?
2a. First choose 5 from 20, then 5 from the remaining 15, then 5 from the remaining 10, leaving 5 for the last team. Ans: (20 | 5) (15 | 5) (10 | 5) = 11732745024 . (I got this from Wolfram Alpha, which understands a command like binomial(20,5).) This is the same as splitting the 20 players into four subsets of size 5, so it is the multinomial coefficient (20 | 5,5,5,5).
2b. This is HW 1/13 #1b: (20 | 5) (15 | 5). Choosing teams A and B leaves 10 students in a third set, so this is the same as (20 | 5,5,10).
2c. To see that the above answers give the formula, write the choose numbers as: (n | k) = n! / k! (n−k)!. Then in 1b, we see by cancellation that:
3. Ans: ((4 | 10)) = (4+10−1 | 10) = 286.
4. A number like 2556 corresponds to a multiset {2,5,5,6}, with 4 objects of 9 possible kinds. Ans: ((9 | 4)) = (9+4−1 | 4) = 495.
5a. A solution like (a,b,c) = (4,5,1) correpsonds to a multiset {1,1,1,1,2,2,2,2,2,3}, in which there are 4 ones, 5 twos and 1 three. Ans: ((3 | 10)) = (12 | 10) = (12 | 2) = 66.
5b. A configuration is determined by the triple (d,m,s), the number of defenders, midfielders, and strikers, with d+m+s = 10. Ans: ((3 | 10)) = 66.
5c. Since 1 goalie, 2 defenders, 2 midfielders, 2 strikers are fixed, the remaining 4 members are determined by (d,m,s) with d+m+s = 4. Ans: ((3 | 4)) = (6 | 4) = 15.
HW:
- Workout with Basic Problems.
A teacher gives an exam to 10 students (Quincy, Rhonda, Sally, ... , Xavier, Ying, Zane).- How many ways could the exams be arranged in a stack? Example: top-to-bottom X,S,U,Y,Q,R,T,V,Z,W.
- Students are listed alphabetically in the grade book, and each receives a grade of A,B,C,D, or F. Example: Q gets C, R gets A, S gets C, ..... How many possible grade lists?
- The teacher writes all the grades in order, highest-to-lowest. Example: A,A,B,B,B,C,C,C,D,F. How many possible grade lists of this kind?
- The teacher gives a gold star to 3 of the students. Example: R,T,W each get a star. How many ways to distribute stars?
- The teacher gives 3 prizes (a pen, a pencil, and a bag of skittles) to three different students. Example: pen to S, pencil to Q, skittles to Y. How many ways to distribute prizes?
- Same as (e), but a given student may receive more than one prize. Example: pen and skittles to U, pencil to V. How many ways to distribute prizes?
- 6 identical gold rings are to be put on 10 fingers, with at most one ring allowed on each. Determine how many arrangements of rings are possible. Example: 11010 10110, where 1 = a ring, 0 = no ring, and the ten positions correspond to fingers. Hint: Transform.
- Same as (g): 6 rings on 10 fingers, but with multiple rings allowed on each finger. Example: 03000 01200, where the number indicates how many rings on each finger.
- In Pascal's triangle, the nth row contains the numerical values of (n | 0), (n | 1), ... , (n | n).
The left and right ends are always (n | 0) = 1 and (n | n) = 1, and each (n | k) is the sum of the entries (n−1 | k−1) and (n−1 | k) above it in the previous row. This reflects the recursive formula:
(n | k) = (n−1 | k−1) + (n−1 | k), which we will discuss in class next time. This exercise explores various properties of this triangle- Compute the first 10 rows of Pascal's triangle using the recursive formula above, adding pairs of entries in each row to get the entry below and between them. (It only takes 1 minute.)
- Re-compute the entries for (6 | 0), (6 | 1), ... , (6 | 6) using our formula (n | k) = nk / k! . Which method of computing (6 | k) is more efficient?
- Starting with (n | k) = nk / k!, show the formula (n | k) = n! / k!(n−k)!. Use this formula to compute (6 | 0), ... , (6 | 6) one more time. Which is more efficient?
- Pascal's triangle has an obvious left-right symmetry in the entries. Explain this using part (c).
- Prove the recurrence formula (n | k) = (n−1 | k−1) + (n−1 | k) by substituting a formula for each binomial coefficient, and checking that the resulting equality is valid.
- Add up each row of Pascal's triangle: that is, compute (n | 0) + (n | 1) + ... + (n | n). Verify the formula from class that this sum is always 2n.
- Now alternately add and subtract each entry in a row: that is, compute (n | 0) − (n | 1) + (n | 2) − ... ± (n | n). Predict a general formula for every n. Can you give any reason or justification why the result is so simple?
- Standard Transformations (See Notes section below.)
- Write out all 24 = 16 subsets of {1,2,3,4}, and under each, write the corresponding binary sequence (a1,..., a4) with ai = 0 or 1, using the Reverse Position Transformation. For example, the set S = {1,4} corresponds to the sequence (1,0,0,1), where the ith position is 1 if i ∈ S, and 0 if i ∉ S.
- Write out all multi-sets with 4 objects of 3 kinds, and under each, write the corresponding list of non-negative whole numbers (a,b,c) with a+b+c = 4, using the Multiplicity Transform. For example, M = {1,1,1,3} corresponds to (3,0,1), since M has 3 ones, 0 twos, and 1 three.
- Add to your table from part (b), by drawing under each multi-set the corresponding bins-and-beans diagram. For example, M = {1,1,1,3} corresponds to [OOO| |O], since there are 3 beans in the first bin, none in the second bin, and one in the third bin.
- Continiung (b) and (c), write the corresponding set of 4 positions out of 6. The diagram [OOO| |O] corresponds to {1,2,3,6}, since the beans occupy the 1st, 2nd, 3rd, and 6th positions inside the brackets [], and the remaining positions are bin-dividers.
1b. Lists of 10 independent entry grades, each with 5 choices. Product Principle: 510
1c. Multi-sets of 10 grades of 5 kinds (with repeats). Requiring increasing order is the same as saying order is irrelevant, since switching the order does not give a new case to count. Basic Problem #4: ((5 | 10)) = (5+10−1 | 10) = (14 | 10) = (14 | 4) = 14×13×12×11 / 4×3×2.
1d. Sets of 3 names out of 10 (order irrelevant). Basic Problem #3: (10 | 3).
1e. Lists of 3 distinct names from 10 (pen-winner, pencil-winner, skittles-winner). Basic Problem #2: 103.
1f. Lists of 3 independent names with 10 choices for each. Product Principle: 103.
1g. The Position Transformation shows this is (10 | 6) = 210.
1h. An arrangement of rings is a list of 10 whole numbers adding up to 6. By the Multiplicity Transform, this corresponds to multi-sets of 6 elements of 10 kinds (think of each ring as a choice of finger 1,2,...,10, with repetition allowed). Ans: ((10 | 6)) = (15 | 6) = 5005.
2a. See HHM p. 139, or type "Pascal's triangle" into Wolfram Alpha.
2b. The triangle is more efficient for computing a whole row, while the formula is better if you only need one value.
2c. The formula (n | k) = n! / k!(n−k)! is very inefficient, since n! is usually much larger than nk. However, this formula is useful for seeing the properties of (n | k), as in the next problem.
2d. There is a left-right mirror symmetry in the entries, which can be proved by noting that (n | k) = n! / k!(n−k)! whereas:
2e. See HHM p. 139.
2f. (n | 0) + (n | 1) + ... + (n | n) = 2n for all n, which follows from the Binomial Theorem next time.
2g. (n | 0) − (n | 1) + ... ± (n | n) = 0 for all n ≥ 1, which also follows from the Binomial Theorem.
3a. Imitate the table at the bottom of Notes 1/11, Position Transformation.
3b,c,d. There are ((3 | 4)) = (6 | 4) = (6 | 2) = 15 multi-sets M, each corresponding to a multiplicity list (a,b,c), a bins-and-beans diagram, and a position set S (see Notes 1/11, Multi-sets). They are:
| M | {1,1,1,1} | {1,1,1,2} | {1,1,1,3} | {1,1,2,2} | {1,1,2,3} | {1,1,3,3} | {1,2,2,2} | {1,2,2,3} | {1,2,3,3} | {1,3,3,3} | {2,2,2,2} | {2,2,2,3} | {2,2,3,3} | {2,3,3,3} | {3,3,3,3} |
| (a,b,c) | (4,0,0) | (3,1,0) | (3,0,1) | (2,2,0) | (2,1,1) | (2,0,2) | (1,3,0) | (1,2,1) | (1,1,2) | (1,0,3) | (0,4,0) | (0,3,1) | (0,2,2) | (0,1,3) | (0,0,4) |
| B&B | OOOOII | OOOIOI | OOOIIO | OOIOOI | OOIOIO | OOIIOO | OIOOOI | OIOOIO | OIOIOO | OIIOOO | IOOOOI | IOOOIO | IOOIOO | IOIOOO | IIOOOO |
| S | {1,2,3,4} | {1,2,3,5} | {1,2,3,6} | {1,2,4,5} | {1,2,4,6} | {1,2,5,6} | {1,3,4,5} | {1,3,4,6} | {1,3,5,6} | {1,4,5,6} | {2,3,4,5} | {2,3,4,6} | {2,3,5,6} | {2,4,5,6} | {3,4,5,6} |
- Vandermonde (n+m | k) = ∑i (n | i)(m | k−i) = ∑i (n | i)(m | m−k+i)
- Specializes with m = k to (n+m | m) = ∑i (n | i)(m | i).
- Thus an m-subset R of [n+m] = [n] ⊔ [m]+n
corresponds to
a subset S ⊂ [n] and a subset T ⊂ [m], both of the same size
via S = R ∩ [n], T+n = [n+1,n+m]∖(R∩[n+1,n+m]) - Especially neat: (2n | n) = ∑i (n | i)2.
HW:
- The Binomial Theorem says that the nth row of Pascal's Triangle gives the coefficients for expanding the nth power of the binomial (x + y):
(x + y)n = xn + (n | 1) xn-1 y + (n | 2) xn-2 y2 + ...+ (n | n-1) x yn-1 + yn For example, the row 1,3,3,1 gives the formula: (x+y)3 = x3 + 3 x2 y + 3 x y2 + y3 .- Compute Pascal's Triangle by hand up to the 10th row: (10|0) = 1, (10|1) = 10, etc. Make sure you know which number is which (n | k).
- Give the formula for (x + y)10 .
- Use the above to explicitly compute 114 and 100110 without a calculator. Hint: 11 = 10 + 1, and 10k has k zeroes. Similarly, 1001 = 1000 + 1, and 1000k has 3k zeroes.
- Deletion Transform proof of the recursive formula: (n | k) = (n−1 | k−1) + (n−1 | k). See Notes 1/22.
- We proved this equality by a transformation, giving a one-to-one correspondence between the objects naturally counted by the left side and those counted by the right side.
- The left side counts k-element subsets S ⊂ {1,2,...,n}.
- The right side counts both k-element and (k−1)-element subsets S' ⊂ {1,2...,n−1}.
- The Deletion Transform takes a set S to the set S' = S\{n}, deleting n if it is present; and leaving S' = S otherwise.
- Define the reverse transformation (the Insertion Transform): given S', what set operations take it back to S? (Your rule can involve cases.)
- Make a table of the Deletion Transform in the case of (6 | 3) = (5 | 2) + (5 | 3). In the first column, list all the sets S, and next to each S write the corresponding S' = S\{6} or S' = S. Write S' in the second column if |S'| = 2, and in the third column if |S'| = 3 . At the end, observe that S' runs over all (5 | 2) sets of size 2 and all (5 | 3) sets of size 3, each just once.
- Extra Credit: Use a multi-version of the Deletion Transform to get a formula for the multi-set number ((n | k)) in terms of smaller multi-set numbers. (Alternatively, you can find this formula by the method of 3(c) below.) Write a version of Pascal's Triangle containing all multi-choose numbers, with entries defined recursively by the formula above.
- Extra Credit: Setting x = 1, y = −1 in the Binomial Theorem for (x+y)n shows that the alternating sum of a row of Pascal's Triangle is always
zero:
(n | 0) − (n | 1) + (n | 2) − (n | 3) + ... + (−1)n(n | n) = 0.
It is possible to prove the above formula using a transformation.
First, we rewrite it without minus signs:
(n | 0) + (n | 2) + (n | 4) + ... = (n | 1) + (n | 3) + (n | 5) + ... The left side counts subsets S ⊂ {1,...,n} with an even number of elements, and the right side counts the subsets with an odd number of elements. To prove the formula, find a reversible rule which takes any even subset on the left to an odd subset on the right (and also specify the reverse rule).
- Extra Credit: Binomials and multi-set numbers
- Reverse the equality ((n | k)) = (n+k−1 | k) to write (n | k) as a multi-set number ((m | k)), where m is some expression depending on n.
- Using part (a), translate the equality (n | k) = (n | n−k) into an equality between multi-set numbers. That is, ((m | k)) is symmetric to what other multi-set number?
- The equality (n | k) = (n | n−k) can be proven by correspondence: the left side counts k-element subsets S ⊂ {1,2,...,n}; the right side counts (n−k)-element subsets S' ⊂ {1,2,...,n}; and the two are related by the transformation S → S' = {1,2,...,n}\S. That is, S' is the complement of S.
Problem: Find a transformation that directly proves the equality between multi-set numbers you found above.
= 104 + 4(103) + 6(102) + 4(10) + 1 = 14641,
Similarly,
= 1,010,045,120,210,252,210,120,045,010,001,
2a. The transformation is defined by two cases: if |S'| = k, then S = S'; if |S'|= k−1, then S = S'∪{n}. We easily see that this reverses the previous transformation, and vice versa.
2b. Here we use 3 rows instead of columns.
| S | {1,2,3} | {1,2,4} | {1,2,5} | {1,2,6} | {1,3,4} | {1,3,5} | {1,3,6} | {1,4,5} | {1,4,6} | {1,5,6} | {2,3,4} | {2,3,5} | {2,3,6} | {2,4,5} | {2,4,6} | {2,5,6} | {3,4,5} | {3,4,6} | {3,5,6} | {4,5,6} |
| S' | {1,2} | {1,3} | {1,4} | {1,5} | {2,3} | {2,4} | {2,5} | {3,4} | {3,5} | {4,5} | ||||||||||
| S' | {1,2,3} | {1,2,4} | {1,2,5} | {1,3,4} | {1,3,5} | {1,4,5} | {2,3,4} | {2,3,5} | {2,4,5} | {3,4,5} |
HW:
- PIE. Recall our Inclusion-Exclusion formula for removing bad subsets B1, B2, B3
from the set A of all objects:
|A \ (B1∪B2∪B3)| = |A| − ∑i |Bi| + ∑i,j |Bi∩Bj| − |B1∩B2∩B3|, where each index runs over 1,2,3, and we have one term for every possible intersection of B1, B2, B3.
Next time, we will generalize this to any number of bad sets Bi ; in particular, the formula for 4 subsets is:|A \ (B1∪…∪B4)| = |A| − ∑i |Bi| + ∑i,j |Bi∩Bj| − ∑i,j,k |Bi∩Bj∩Bk| + |B1∩B2∩B3∩B4| , where the indices run over all numbers with 1 ≤ i < j < k ≤ 4. Here the summation notation ∑i |Bi| means sum up the value of |Bi| for i = 1,2,3,4; namely, a compact way to write:∑i |Bi| = |B1| + |B2| + |B3| + |B4|. Similarly ∑i,j means sum up over all pairs of values (i,j) = (1,2), (1,3), (1,4), (2,3), (2,4), (3,4).
Problem: Write out this formula without summation signs, listing each pairwise and triple intersection. How many terms are there of each kind? How many terms total? How could you have predicted the number of terms? - 6 rings are to be put on 10 fingers. Determine how many arrangements of rings are possible under each assumption.
- The rings are identical (plain gold bands), with at most one allowed on each finger. Example: 11010 10110, where 1 = a ring, 0 = no ring, and the 10 positions correspond to fingers. Hint: Positive counting.
- The rings are identical, with any number allowed on each finger. Example: 03000 01200, where the number indicates how many rings on each finger. Hint: Positive counting.
- The rings are identical, with at most one allowed on each thumb, any number on the other fingers. Hint: PIE with A = {all arrangements from part (b)}, and forbidden sets B1 = {arrangements with at least 2 rings on right thumb}, B2 = same for left thumb. Alternatively, use positive counting by cases.
- The rings are identical, with at most two allowed on each finger. Hint: Here, positive counting is not practical. Use PIE, with A = {all arrangements from part (b)}, B1 = {at least 3 rings on finger 1},..., B10 = {at least 3 rings on finger 10}. There are 10 forbidden sets, but the PIE formula is still manageable, because...
- The rings are distinguishable (Diamond, Emerald, Ruby, Sapphire, Turquoise, Catseye), with at most one on each finger. Example: 0R0E0 T0CSD. Hint: Positive counting using a Position Transform: e.g. the arrangement 0R0E0 T0CSD puts D,E,R,S,T,C into positions (10,4,2,9,6,8).
- The rings are distinguishable, with at most one on each finger, but the Diamond and Emerald do not fit on either thumb.
- Extra Credit: The rings are distinguishable, with any number on each finger, and the order of the rings on one finger matters. (That is, D below R is different from R below D.) Hint: First put on 6 identical rings, then replace each with one of the jewelled rings. Another method: Put the D,E,R,S,T,C rings on one by one, and keep track of how many choices are available at each step.
- Extra Credit: There are k distinguishable rings and n fingers, with at least one on each finger (and again the order on each finger matters). Hint: Use the previous part, and PIE.
- Six different jobs (J1,...,J6) are assigned to 6 people (P1,...,P6), one job to each.
- How many ways to assign the jobs? That is, count all possible job rosters.
- Impose the restriction that P1 cannot do J1, P2 cannot do J2, and P3 cannot do J3 (but P4,P5,P6 can do any job). How many allowed job rosters?
Hint: PIE with A = {all job rosters} and forbidden sets B1 = {rosters with P1 doing J1}, and similarly B2, B3. - How many ways to assign the jobs, with the restriction that P1 cannot do J1 or J2, and P2 cannot do J3 or J4?
Hint: PIE with A = {all job rosters} and 4 forbidden sets.
2a. The Position Transformation shows this is (10 | 6) = 210.
2b. An arrangement of rings is a list of 10 whole numbers adding up to 6. By the Multiplicity Transform, this corresponds to correspond to multi-sets of elements of 10 kinds (think of each ring as a choice of finger 1,2,...,10, with repetition allowed). Ans: ((10 | 6)) = (15 | 6) = 5005.
2c. To count B1, begin by putting 2 rings on the right thumb, then distribute the remaining 4 rings on any of the 10 fingers (including extras on the right thumb). Thus, |B1| = ((10 | 4)), and the same for |B2|. Ans: ((10 | 6)) − ((10 | 4)) − ((10 | 4)) + ((10 | 2)).
2d. Since there are only 6 rings total, we cannot have an intersection of more than 2 subsets Bi∩Bj . Ans:
2e. Write an arrangement by recording which finger has D, which has E, which has R, etc. Then the arrangements correspond to lists of 6 distinct numbers from {1,2,...,10}. Ans: 106.
2f. PIE with A = {arrangements of D,E,R,S,T,C on 10 fingers, at most 1 per finger} and
B1 = {arrangements with D on left thumb},
B2 = {arrangements with D on right thumb},
B3 = {arrangements with E on left thumb},
B4 = {arrangements with E on right thumb}.
Ans: 106 − 4×95 + 2×84.
Positive counting: There are 8 choices for D, 7 for E, 8 for R, 7 for S, 6 for T, and 5 for C. Ans: 8×7×84.
3a. A job roster is a list of all the jobs in some order. Ans: 6! .
3b. Note |B1| = 5! since we assign the remaining 5 jobs to 5 people. Similarly for the rest of the terms in PIE formula. Ans: 6! − 3×5! + 3×4! -3!
3c. PIE with A = {all job rosters}, B1 = {P1 doing J1}, B2 = {P1 doing J2}, B3 = {P2 doing J3}, B4 = {P2 doing J4}.
Then |B1| = 1×5×4×3×2×1, figuring the number of choices for Person 1, Person 2, etc. Similarly for |B2| , |B3|, |B4|.
Also |B1∩B3| = 1×1×4×3×2×1 , and similarly for |B1∩B4|,
|B2∩B3|, |B2∩B4|, but |B1∩B2| = |B3∩B4| = 0. All triple intersections are empty.
Ans: 6! − 4×5! + 4×4!
HW:
- Another problem on job rosters of 6 people assigned 6 jobs (as in HW 1/25 #3). Suppose P1 cannot do J1 or J2, and P2 cannot do J2 or J3. How many allowed rosters?
- You have 10 friends {1,...,10}, and you invite a set of 5 to dinner. However, some pairs hate each other, and cannot be invited together: they are {1,2), {2,3}, and {3,4}. How many allowed sets of guests?
- Another problem on rings: 15 identical rings are to be put on 10 fingers. Count the ways to arrange the rings under the following conditions. In each case, use both positive counting and PIE to get the answer.
- There is at least one ring on each finger.
- There are exactly one or two rings on each finger.
- In class, we discussed the Derangement Problem (Secret Santa). See also HHM p. 160.
- Let dn be the answer to this problem: the number of permutations (rearrangements or orderings) of n objects such that no object is returned to its previous place.
- In terms of Prob 1 above, this is the same as job rosters for n people in which Person i cannot do Job i, for all i = 1,...,n.
- Example: d3 = 2, since the derangements of {1,2,3} are: (2,3,1) and (3,1,2); on the other hand, (3,2,1) is not a derangement, since 2 is in position 2.
- In class, we used PIE with A = {all permutations} and Bi = {permutations fixing the ith position}, to get the formula:
dn = n! − (n | 1) (n-1)! + (n | 2) (n-2)! − (n | 3) (n−3)! + ... + (−1)n .
- Show that you can re-write this as:
dn = n! (1 − 1 + 1/2! − 1/3! + ... + (−1)n/n!) . - Secret Santa: Suppose n = 10 people put their names in a bag, and each draws out a name at random. What is the probability that no one draws his own name? Also compute this for n = 20.
- Prove that if n is very large, the probability that no one gets his own name does not approach 0, as one might expect, but rather 1/e, where e = 2.718... is the base of the natural logarithm. Hint: Use the Taylor series ex = 1 + x + x2⁄2! + x3⁄3! + ...
- Extra Credit: Stirling partition numbers. See Notes 1/27 below.
- Show that {n | 1} = {n | n} = 1 and {n | 2} = 2n−1 − 1
- Use the definition to find a very simple formula for {n | n−1}.
- Super challenge: The Deletion Transform allows us to discover and/or prove Pascal Triangle type recurrence formulas for the choose numbers (n | k) and the multi-choose numbers ((n | k)). Adapt this argument to discover and prove a recurrence for Stirling partition numbers, of the form:
{n | k} = a{n−1 | k−1} + b{n−1 | k}, where a and b are some coefficients which might involve n or k. The point is: if we remove the element n from the partiton S1∪...∪Sk = {1,..,n} to obtain a new partiton S1'∪...∪Sk' ={1,...,n−1}, we obtain two cases. In each case, what information must we retain to be able to recover the orginal partition? Figure it out in an example.
Check your recurrence formula by constructing the analog of Pascal's Triangle, and seeing if the entries match the explicit PIE formula for {n | k}.
2. PIE: A = {sets of 5 from 10}, B1 = {sets containing 1,2}, B2 = {sets containing 2,3}, B3 = {sets containing 3,4}. Clearly |A| = (10 | 5), and |Bi| = (8 | 3) since if two guests are fixed, this leaves 5−2 more to choose from 10−2. Similarly |B1∩B2| = (7 | 2), etc. Ans: (10 | 5) − (3 | 1)(8 | 3) + (7 | 2) + (6 | 1) + (7 | 2) − (6 | 1) = 126.
3a. PIE:
- A = {all arrangements of 15 rings on 10 fingers}
- Bi = {finger i has no ring} for i = 1,..., 10.
- Count: ((10 | 15)) − (10 | 1) ((9 | 15)) + (10 | 2) ((8 | 15)) − ... − (10 | 9) ((1 | 15)) = 2002.
3b. PIE:
- A = {all arrangements of 15 rings on 10 fingers}
- Bi = {finger i has no ring} and B'i = {finger i has ≥ 3 rings} for i = 1,...,10 (20 bad sets in all).
PIE/Postive hybrid:
- A = {all arrangements of 5 remaining rings on 10 fingers},
- Bi = {finger i has ≥ 2 of the 5 rings} for i = 1,..., 10
- Count: ((10 | 5)) − (10 | 1)((10 | 3)) + (10 | 2)((10 | 1)) = 252.
Moral: Positive counting gives the simplest answer, if you can find the tricks to transform the data into a form that allows it.
4a. In the original formula for dn, write out (n | k) = n! / k!(n−k)! ; then factor out n! and cancel (n−k)! in each term to get the desired formula.
4b. For both cases the answer is dn/n! ≅ 0.36788 up to many digits of accuracy.
4c. From the formula, the probabability dn/n! = 1 − 1 + 1/2! − 1/3! + ... + (−1)n/n!, which is the first n terms of the formula for e−1 = 1/e. Since the Taylor series converges for all x, this approaches 1/e as n→ ∞.
HW:
- In class, we used the Sieve of Eratosthenes to count the primes less than 100. That is, we said that n ≤ 100 is prime if and only if n is not a multiple of 2,3,5, or 7 (the primes ≤ √100 = 10). (Of course, we must also count 2,3,5,7 themselves as primes.)
To count the numbers with these restrictions, we used PIE with:
- A = {2,3,4,5,6,...,100}
- A1 = {multiples of 2}
- A2 = {multiples of 3}
- A3 = {multiples of 5}
- A4 = {multiples of 7}
- Write out the resulting PIE formula from class, and evaluate it. Also, add 4 in order to count 2,3,5,7 themselves as primes. This tells the number of primes.
- Now, find the prime numbers themselves by a sieve method on this table. First, cross out 1 (since it does not count as prime). Next, circle the smallest remaining entry 2 (the first prime) and cross out all its multiples 4,6,8,.... Now repeat: circle the first remaining number 3 and cross out all its multiples 6,9,12,... Doing this again for 5 and 7, the remaining numbers are all prime, since any composite ≤ 100 has a factor of 2,3,5 or 7. Does your result agree with the result of part (a)?
- Extra Credit: Let p(n) denote the number of primes ≤ n, so that part (a) computed p(100) = 25. There is no known formula for p(n), but the Prime Number Theorem gives an amazing approximation which gets more and more accurate as n gets large (i.e. it is an asymptotic formula).
Look up and summarize a reference about the Prime Number Theorem. What is the expected approximation for p(100), and how well does it match the exact value? Plot some values comparing the true p(n) to the approximation. - Extra Credit: The sequence of primes is quite mysterious. Could there be a "formula for primes", meaning a fairly simple function f(n) whose values f(1), f(2), f(3),... are all prime? For example, the polynomial f(n) = n2 + n + 1 gives f(1) = 3 , f(2) = 7 , f(3) = 13 , but f(4) = 21 = 3×7, so this does not work. Could any polynomial f(n) work? What about Euler's polynomial n2 − n + 41?
The number of elements of A not divisible by 2,3,5,7 is thus:
= 99 − 50 − 33 − 20 − 14 + 16 + 10 + 7 + 6 + 4 + 2 − 3 − 2 − 1 − 0 + 0 = 21.
Adding 4 to account for 2,3,5,7 themselves, this gives 25 primes less than 100.
1b. The 25 primes less than 100 are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 .
HW
- Binomial Theorem
- Multiply out (x+y)3 using the distributive law, but without simplifying or collecting terms. Make a table of how the 8 terms xxx + xxy + xyx + ... + yyy correspond to subsets S⊂{1,2,3}. Do this so that terms which are algebraically equal (like xxy, xyx, yxx) are adjacent in the table.
- Do the same for (x+y)4, getting 16 terms.
- Logical algebra of multisets. Suppose you have 2 apples and 2 bananas and you put any or all of them in your lunch bag, for example 2 apples and 0 bananas (a multi-set). What are all the possibilities for the contents of the bag?
- Figure this by letting "0A" stand for the choice of no apples, "1A" the choice of one apple, etc., and logically expanding the expression:
(0A or 1A or 2A) and (0B or 1B or 2B) using the logical distributivity rule from the notes. Expand until you have an expression like:
(0A and 0B) or (0A and 1B) or .... or (2A and 2B). Match each case at the end to a particular lunch-bag multiset. For example, (2A and 2B) is the multiset M = {A,A,B,B}. - Translate the entire logical computation in (a) into the language of algebra, replacing 0A, 0B by x0; 1A, 1B by x1; 2A, 2B by x2; "or" by + ; "and" by ×. Start with
(x0 + x1 + x2) (x0 + x1 + x2) and expand using algebraic distributivity. Collect like terms to get a polynomial a0 + a1 x +...+ a4 x4 .
Question: What is the combinatorial meaning of the coefficients a0,...,a4? That is, what do these values count about ways of filling the bag? - Now expand f(x) = (1 + x + x2)2 again, this time using the binomial theorem (a+b)2 = a2 + 2ab + b2 twice: first with a = 1, b = x + x2, and then again with a = x, b = x2. Thus, re-compute the coefficients a0,...,a4 using only algebra.
- Figure this by letting "0A" stand for the choice of no apples, "1A" the choice of one apple, etc., and logically expanding the expression:
1a. (x+y)3 = (xx + xy + yx + yy)(x + y) = xxx + xyx + yxx + yyx + xxy + xyy + yxy + yyy.
| term | xxx | xxy | xyx | yxx | xyy | yxy | yyx | yyy |
| S | {} | {3} | {2} | {1} | {2,3} | {1,3} | {1,2} | {1,2,3} |
Thus, there are clearly (3|1) terms which are algebraically equal to x2y, and (3|2) terms equal to xy2.
1b. To get (x+y)4, start with the previous result and multiply (xxx + xyx + yxx + yyx + xxy + xyy + yxy + yyy)(x + y) to get 16 terms. Check these off one by one when you put them in the table. The term x4 comes from the set {}, the terms algebraically equal to x3y come from the sets with 1 element, the terms equal to x2y2 come from the sets with 2 elements, etc.
2a. The final expanded expression has terms (outcomes) corresponding to the multisets as follows:
| term | 0A & 0B | 0A & 1B | 0A & 2B | 1A & 0B | 1A & 1B | 1A & 2B | 2A & 0B | 2A & 1B | 2A & 2B |
| M | {} | {B} | {B,B} | {A} | {A,B} | {A,B,B} | {A,A} | {A,A,B} | {A,A,B,B} |
2b. Multiply out (x0 + x1 + x2)2 to get:
2c. (1 + (x+x2))2 = 1 + 2(x+x2) + (x+x2)2 = 1 + 2x + 2x2 + (x2 + 2xx2 + x4) = 1 + 2x + 3x2 + 2x3 + x4.
HW:
- A trial example for the Method of Generating Funcitons
(HHM p. 166 #2). A drawer contains some beads:
3 Green, 4 Blue, 5 Red.
Let a be the number of ways to select a handful of 6 beads.
Example: 3 Green, 3 Red.
Find a by the Method of Generating Functions.
- Step 0: Think of a as one of a sequence of problems a0, a1, a2,..., an. How high does the sequence go: what is n?
- Step 1: Let f(x) = a0 + a1 x + a2 x2 + ...+ a12x12 be the generating function coefficients ak. We do not know these ai, so we do not yet know f(x). But use the Product Principle for a0 + a1 + ... + an:
(choose any number of beads from drawer) ⇔ (0G or 1G or 2G or 3G) and ... where 0G means no Green, means 1 Green, etc.
Now translate this logical equivalence into algebra: replace each logical term with an algebraic one, as in the Notes 2/3. The left-hand side is replaced with f(x), which encodes all possible handfuls. The right-hand side is a product, which multiplies out so that each term algebraically equal to xk corresponds to a particular handful of k beads; thus the coefficient of xk is indeed ak. Therefore, f(x) is equal to an explicit algebraic product. - Step 2: Given the formula from Step 1, use algebra to expand f(x) and find the coefficient of x6, which is the number a = a6 which we originally wanted. In this case, there is no algebraic trick which can help expand, so type in the formula for f(x) into the computer algebra website Wolfram Alpha, which will expand out for you. The explicit coefficients you obtain will be the values of ak.
- HHM p. 166 #3. Now the drawer of beads contains 10 red, 8 blue, 11 lightgreen.
Let ak be the number of ways to select a handful of k beads with one of the restrictions below.
Do Step 1 as above. For Step 2, you may once again use the algebra website.
- No restrictions on the handful.
- Restriction: you must take an even number of reds, an odd number of blues, and a prime number of greens.
- Restriction: you must take exactly 2 reds, at least 5 blues, at most 4 greens.
- Re-do the example of 5-card hands from a double deck from class (see Ch 2.6.1). We did Step 0: ak is the number of k-card hands from the double deck. Example: a104 = 1 since there is only 1 hand with all 104 cards.)
In Step 1, we used the Product Principle to find the generating function f(x) = (1 + x + x2)52.
- Now do Step 2. Use the Binomial Theorem for (a + b)52 applied to a = 1, b = (x+x2); then use it again applied to (x + x2)m. Since we are only looking for a5, you only need to find all the x5 terms, which come from (52 | 3) (x + x2)3, (52 | 4) (x + x2)4, and (52 | 5) (x + x2)5. Your result will be a specific formula for a5 in terms of binomial coefficients, found purely by algebra, with no reasoning about hands except for the Product Principle in Step 1.
- Look at your formula for a5, and explain what each of the terms means combinatorially.
- Compute a6 by the same method, and explain the result combinatorially.
- Extra Credit: Is each of the above hands equally likely, assuming we deal in the usual way from the double deck? Actually, no. Explain.
This means we cannot use this model to compute probablilities by counting. What model should we use instead?
Step 1: (choosing a handful of beads) ⇔ (0G or 1G or 2G or 3G) and (0B or 1B or ... or 4B) and (0R or 1R or ... or 5R) .
f(x) = (1+x+x2+x3) (1+x+x2+x3+x4) (1+x+x2+x3+x4+x5)
Step 2. f(x) = 1 + 3x + 6x2 + 10x3 + 14x4 + 17x5 + 18x6 + 17x7 + 14x8 + 10x9 + 6x10 + 3x11 + x12. Thus a6 = 18.
2a. f(x) = (1+x+...+x10) (1+x+...+x8) (1+x+...+x11)
2b. f(x) = (1+x2+x4+x6+x8+x10) (x+x3+x5+x7) (x2+x3+x5+x7+x11)
2c. f(x) = x2 (x5+x6+x7+x8) (1+x+x2+x3+x4)
3a. f(x) = 1 + (52 | 1)(x+x2) + (52 | 2)(x+x2)2 + (52 | 3)(x+x2)3 + (52 | 4)(x+x2)4 + (52 | 5)(x+x2)5 + ...
We want to extract the x5 terms. Now (x+x2)m has lowest term xm, highest term x2m, so we only need to look at:
3b. In the expression a5 = (52 | 3)(3 | 2) + (52 | 4)(4 | 1) + (52 | 5)(5 | 0), the last term (52 | 5) clearly counts 5-card hands with no repeated cards from the 52. The middle term (52 | 4)(4 | 1) means choose 4 distinct cards from 52, then choose one of them to repeat. The term (52 | 3)(3 | 2) means choose 3 distinct cards from 52, then choose 2 of them to repeat. This covers all possibilities of 0,1, or 2 repeated cards.
Taylor series review: Khan Academy, Wikipedia.
HW:
- Review of Taylor Series. Let f(x) = a0 + a1x + a2x2 + ... + anxn be a polynomial function.
Here a0, a1,..., an are some constants which are the coefficients.
- Note that a0 = f(0), since substituting x = 0 makes all other terms vanish.
Note also that the derivative of f(x) is:
f '(x) = a1 + 2 a2 x + 3 a3 x2 + ... + n an xn−1. Substituting x = 0, we find a1 = f '(0). Find a similar formula for a2, and for a general ak. Hint: Compute f (k)(x), the k-th derivative of f(x). - This gives a new way to compute any row of Pascal's Triangle, for example n = 10. We think of (10 | k) as the coefficient ak in f(x) = (1+x)10 = a0 + a1x + a2x2 + ... + a10x10. Use the formula from part (a) to compute ak = (10 | k). Hint: Use the Chain Rule to differentiate (1+x)10.
- Taylor's formula in calculus says that most common functions f(x) can be expressed as Taylor series (infinite polynomials):
f(x) = a0 + a1 x + a2 x2 + .... = ∑k=0∞ ak xk . This means that as you add more and more terms on the right (with x fixed), it becomes a better and better approximation to the value f(x) on the left. The equation might be valid only for small x, such as |x| < 1.
Problem: Do some research to find some functions which can't be approximated by Taylor series. - The coefficients of a Taylor series are given by the same formula as for polynomials above, since a polynomial is its own Taylor series: ak = f (k)(0) / k! , where f (k)(0) means the kth derivative of f(x) at x = 0.
Problem: Compute the Taylor series for f(x) = ex, which is its own derivative: f '(x) = f(x). - Compute the Taylor series for 1/(1−x) = (1−x)−1.
- Compute the Taylor series of f(x) = sin(x) , using the derivatives sin'(x) = cos(x) and cos'(x) = −sin(x). That is, compute the coefficients a0, a1, a2,...., until you see the pattern. Write the answer in "dot-dot-dot" notation (writing out enough terms to make the pattern clear, then "..."), and also in terms of summation notation. (For summation notation, your exponent should be x2k+1 since the even terms are zero.)
- Approximate sin(π/6) by substituting x = π/6 into your Taylor series, and adding the terms up to x5. How good is the approximation?
- Note that a0 = f(0), since substituting x = 0 makes all other terms vanish.
Note also that the derivative of f(x) is:
- Practice with geometric series
- Compute the Taylor series of the function f(x) = 1/(1−ax), where a is a constant. Hint: You can use Taylor's Formula directly, or substitute ax in place of x in the known geometric series formula.
- Compute the Taylor series of f(x) = 1/(x+b), where b is a constant.
- Find a simple formula for the generating series f(x) = ∑k ≥ 1 k xk . Hint: Differentiate known series.
- Use geometric series to find the value of the infinite repeating decimal 0.1111.... Hint: Write out the meaning of the decimal in terms of 1/10, 1/100,....
- Denote a general decimal number as: 0.d1d2d3... where dk are digits between 0 and 9. Use geometric series to evaluate a general repeating decimal as a fraction: 0.d1d2...dnd1d2...dn... = a/b, where a and b are whole numbers. Hint: Use the whole number D = d110n−1 +d210n−2 + ... + dn-110 + dn .
- Problem: What is the probability of getting k heads in 10 tosses of a coin (which lands heads or tails each time)?
Do this problem by the Method of Generating Functions.
Step 1: Write an algorithm which describes all possible outcomes of 10 tosses as a sequence of choices separated by and. Translate this logical algorithm into an algebraic expression for the generating function f(x) = ∑k akxk.
Step 2: Expand f(x) by the Taylor coefficient formula, and explicitly find the coefficient of xk, giving a formula for ak. Can you explain the answer by combinatorial reasoning alone?
Finally, find the probability asked for in the problem. - Consider a triple deck with three identical copies of 52 distinct cards.
Find the number of distinct 5-card hands from the triple deck
the way we did the double deck problem in class.
Hint: Use the factorization: 1+x+x2+x3 = (1+x)(1+x2) to get an especially simple answer for a5.
Extra Credit: Explain this answer by combinatorial reasoning.
1b. f (k)(x) = 10k(1+x)10−k since (1+x)' = 1. Thus (10 | k) = ak = f (k)(0) / k! = 10k / k!. This is not really a new formula, but a way to get the old formula purely through algebra, without reasoning much about sets.
1c. A function which is badly behaved near x = 0 might not have a Taylor series. For example, f(x) = 1/x has a vertical asymptote, and cannot be approximated by polynomials. Also, f(x) = |x| is not differentiable at x = 0, we cannot apply the formula for ak, and there is no Taylor series. In fact, no polynomial function looks like |x| very close x=0, since every polynomial has a smooth graph, whereas the graph of |x| has a corner.
1d. f (k)(x) = ex, so f (k)(0) = 1. Hence ak = 1 / k! and ex = 1 + x + x2 / 2! + x3 / 3! + .... This converges for all x, and so a finite number of terms give an approximation to ex.
1e. f (k)(x) = k! (1−x)−(k+1), so ak = k! / k! = 1 and 1/(1−x) = 1 + x + x2 + x3 + ..., an infinte geometric series, which converges for |x| < 1.
1f. sin(x) = x − x3/3! + x5/5! − x7/7! + ...
1g. sin(π/6) = 0.5. The polynomial p(x) = x − x3/3! + x5/5! gives p(π/6) = 0.48, which is pretty close. The point of the Taylor polynomial is that it computes a good approximation of sin(θ) for any given angle θ (provided θ is not too large), for which there is no exact answer.
2a. 1/(1−ax) = 1 + (ax) + (ax)2 + (ax)3 + ... = 1 + ax + a2x2 + a3x3 + ...
2b. 1/(x+b) = 1 / b(1−(−x/b))
= 1/b (1 − x/b + x2/b2 − x3/b3 + ...)
= 1/b − x/b2 + x2/b3 − x3/b4 + ...
2c. We know 1 / (1-x) = ∑k xk.
Differentiating both sides gives: 1/(1−x)2
= ∑k≥1 k xk−1. Hence
x / (1−x)2 = ∑k≥1 k xk
2d. 0.11111... = 1/10 + (1/10)2 + (1/10)3 + ... = − 1 + 1/(1 − 1/10) = 1/9.
2e. The decimal is 10−nD (1 + 10−n + (10−n)2 + ...) = 10−nD / (1 − 10−n) = D / (10n − 1). Example: 0.325325... = 325/999.
3. Step 1: (any outcome of 10 tosses) ⇔ (T1 or H1) and ...
and (H10 or H10), where Ti means the ith toss is heads,
Hi means the ith toss is tails.
We translate Ti into x0 because a tail adds 0 to the number of heads; and we translate Hi into x1, giving:
f(x) = (x0 + x1)10
= (1 + x)10.
Step 2: Taylor's Formula in #1b above gives:
ak = 10k⁄k! = (10 | k).
The number of outcomes of 10 tosses is 210 by the Product Principle, which is a simplified version of our computation of f(x) with x = 1. The probability of k heads is thus (10 | k) / 210.
The result ak = (10 | k) is explained combinatorially by the Position Transform (Notes 1/20): each outcome with k heads is equivalent to the k-element set of positions of the k heads out of the 10 possible positions.
4. Step 0: Let ak count the possible k-card hands from a triple deck.
Step 1: For each distinct card C, we have the choice (0C or 1C or 2C or 3C). For the 52 distinct cards, this produces f(x) = (1+x+x2+x3)52
Step 2: Use the Binomial Theorem to expand:
= (1+x)52(1+x2)52,
= ( ∑52k=0 (52 | k) xk ) ( ∑52j=0 (52 | j) x2j )
so a5 = (52 | 5) + (52 | 3)(52 | 1) + (52 | 1)(52 | 2).
This must have a combinatorial explanation, corresponding to three cases
with a product principle for each, but it is not obvious just how to do this.
Once again, Generating Functions substitute algebra for fairly subtle combinatorial thinking.
HW:
- Recovering known formulas for choose and multi-choose numbers
- For n = 10, define ak = (10 | k) = the number of ways to choose a set of k distinct elements from 10. Compute ak by Generating Functions, as we did in class. The generating function f(x) = ∑k = 010 akxk will be a polynomial with highest term x10. For Step 2, use Taylor's Formula ak = f(k)(0) / k! .
Note: Here we forget how to compute (n | k). The point is to re-discover the known formula. - Same for the multi-choose numbers ak = ((10 | k)). The generating function will be an infinite Taylor series. For Step 1, you will need the known power series 1 + x + x2 + ... = 1/(1−x). For Step 2, again use Taylor's Formula. The result for ak does not look exactly like the known formula for ((n | k)). Show they are equal.
- Repeat the above for arbitrary n instead of n = 10. Give an alternative formula for ((n | k)), in terms of the rising power notation nk = n(n+1)(n+2)...(n+k−1), which rises from n with k factors.
- For n = 10, define ak = (10 | k) = the number of ways to choose a set of k distinct elements from 10. Compute ak by Generating Functions, as we did in class. The generating function f(x) = ∑k = 010 akxk will be a polynomial with highest term x10. For Step 2, use Taylor's Formula ak = f(k)(0) / k! .
- Practice for Step 2 of the Method: Find the Taylor series of the following functions as explicitly as possible, simplifying the coefficients as much as possible. Hint: Modify the known series at the end of Notes 1/30, substituting appropriate expressions for z.
(a) f(x) = 1/(1−x4) (b) f(x) = 1/(1−x)4 (c) f(x) = 1/(1−x2)2 (d) f(x) = x2/(1−x)4 (e) f(x) = (5−x)/(1−x)2 - Difference of powers trick
- Verify the formula:
an − bn = (a − b) (an−1 + an−2b + an−3b2 + ... + bn−1) by multiplying out the right side and cancelling terms. - Find the Taylor series of: f(x) = 1 / (1−x)(1−x2). Hint: Use the trick of multiplying top and bottom by 1+x, then simplifying the bottom with the difference-of-squares formula to get (1−x2)2. Finally use the known Taylor series 1/(1−z)2 = ∑k≥0 ((2 | k))zk with z = x2.
- Do the same for 1 / (1−x)(1−x3). Hint: Multiply top and bottom by (1+x+x2), and use (1+x+x2)(1−x) = 1−x3.
- Verify the formula:
- Making Change Problem. Let Nk be the number of ways to make change for k cents with pennies (1¢) and nickels (5¢). For example,
N10 = 3, which counts the cases: 5+5 (two nickels), 5+1+1+1+1+1 (nickel and 5 pennies), and 1+...+1 (10 pennies).
- Compute an explicit formula for Nk by the Method of Generating Functions. Hint: For Step 1, use the Product Principle for a handful of change with any value. Replace each basic choice (how many pennies, how many nickels) by xk, where k is the cents value of that choice. For Step 2, use the Difference of Powers trick to get the denominator to be (1−x5)2, which can be expanded by a known series; finally multiply it all by the polynomial in the numerator, which shifts around the powers of x.
- Explain the formula for Nk by purely combinatorial reasoning.
- Rolling dice. A standard cubical die has faces numbered 1,2,...,6.
- Let ak be the number of ways to roll a total of k = 2,3,...,12 with two dice. For example, you can roll a 3 as 1+2 or 2+1, so a3 = 2. There is a total of 6×6 = 36 possible rolls, so the probability of k = 3 is 2/36.
Compute a2,..., a12 by Generating Functions, and make a table of probabilities for the rolls.
Step 1: Use the product principle see an arbitrary roll as a pair of independent choices (the value of each die). Translate this into algebra, replacing each basic choice which adds m to the total by xm.
Step 2: Use Wolfram alpha to expand f(x) into a series. - Sicherman dice are a pair of cubical dice with special number labels instead of the standard 1,2,...,6: one has labels 1,2,2,3,3,4, the other has 1,3,4,5,6,8. Show that the probability of rolling k = 2,...,12 with these dice is the same as the probability for a standard pair.
Extra Credit: Explain how to discover the Sicherman dice by getting Wolfram alpha to factor the generating function for standard dice from part (a). - Do the same as part (a) for rolls of 3 dice.
- Now part (c) without a computer. For Step 2, use the identity x+x+...+x6 = x(1−x6) / (1−x), then expand using the Binomial Theorem for positive and negative powers.
- Extra Credit: Use generating functions to find a formula for the number of ways to roll k with n dice. Hint: You may use the definition ((n | k)) = 0 for k < 0.
- Let ak be the number of ways to roll a total of k = 2,3,...,12 with two dice. For example, you can roll a 3 as 1+2 or 2+1, so a3 = 2. There is a total of 6×6 = 36 possible rolls, so the probability of k = 3 is 2/36.
Step 1: Construct all sets S by an algorithm based on the Product Principle:
which translates to algebra as:
f(x) = ∑k≥0 akxk = (x0 + x1) (x0 + x1) ... (x0 + x1).
Here each basic choice i∉S adds 0 to the size of S, so we replace it with x0, while i∈S adds 1 to the size of S, so we replace it with x1. Simplifying, we have: f(x) = (1+x)10.
Step 2: Here we do not use the Binomial Theorem to expand f(x), because this just gives the set-counting number we started with: ak = (10 | k). The point here is to re-discover the algebraic formula for (10 | k), so we use the most basic tool for finding coefficients of Taylor series, the general formula ak = f(k)(0) / k!. We have f '(x) = 10(1+x)9, f ''(x) = 10(9)(1+x)8,..., f(k)(x) = 10k(1+x)10−k, so that ak = 10k(1+0)10−k / k! , meaning (10 | k) = 10k / k! .
Success! The Generating Function Method gives the formula for counting sets. Look up the combinatorial argument we used to show this formula: it was not easy.
1b. Step 0: ak = ((10 | k)) = # multi-sets M with k elements of n kinds.
Step 1: Construct all multi-sets M by an algorithm based on the Product Principle:
... and ( 0(10's in M) or 1(10's in M) or 2(10's in M) or ... )
This has infinitely many choices, because there are infinitely many possible M's (for example, choose any number of 1's). This translates to algebra as:
Step 2: Again using ak = f(k)(0) / k!, we have: f(x) = (1−x)−10,
f ''(x) = 10(−11)(1−x)−12(−1) = 10(11)(1−x)−12
f(k)(x) = 10k(1−x)−(10+k)
This matches our previous combinatorial formula based on the Bins-and-Beans Transformation, because: ((10 | k)) = (10+k−1 | k) = (10+k−1)k / k! = (10+k−1)(10+k−2)...(11)(10) / k! = 10k / k!
1c. The case of general n is just the same, giving the formulas (n | k) = nk / k!
and ((n | k)) = nk / k! .
An interesting algebraic parallel, which only came out with our use of the Generating Function Method!
2a. Geometric series 1/(1−z) = 1 + z + z2 + ... with z = x4, so f(x) = 1 + x4 + x8 + x12 + ... = ∑k≥0 x4k , and a4k = 1, all other am = 0.
2a. Geometric series 1/(1−z) = 1 + z + z2 + ... with z = x4, so f(x) = 1 + x4 + x8 + x12 + ... = ∑k≥0 x4k , and a4k = 1, all other am = 0.
2b. Binomial with negative exponent: f(x) = ∑k≥0 ((4 | k)) xk, so ak = ((4 | k)) = (k+1)(k+2)(k+3)/6 .
2c. Binomial with negative exponent: f(x) = ∑k≥0 ((2 | k)) x2k, so a2k = ((2 | k)) = k+1, am = 0 for m odd.
2d. f(x) = x2 (1 + ((4 | 1))x + ((4 | 2))x2 + ...) = ((4 | 0))x2 + ((4 | 1))x3 + ((4 | 2))x4 + .... = ∑k≥2 ((4 | k−2)) xk, so ak = ((4 | k−2)) = (k−1)k(k+1)/6.
2e. f(x) = (5−x) ∑k≥0 ((2 | k)) xk = ∑k≥05 ((2 | k)) xk − ∑k≥0 ((2 | k)) xk+1
= ∑k≥05 ((2 | k)) xk − ∑k≥0 ((2 | k−1)) xk = ∑k≥0 [5 ((2 | k)) − ((2 | k−1))] xk ,
so ak = 5 ((2 | k)) − ((2 | k−1)) = 5(k+1) − k = 4k + 5.
3a. This follows just from multiplying out and cancelling. Alternatively, you can deduce it from (1−xn) / (1−x) = 1 + x + x2 + ... + xn−1 (the finite geometric series summation from an old HW), with x = b/a, after clearing denominators.
3b. Use (1+x)(1−x) = 1−x2 to massage the denominator into the form 1 / (1−x2)2. Then use the known series formula: 1 / (1−z)2 = ∑k≥0 ((2 | k))zk, with z = x2.
= (1+x) / (1−x2)2 = (1+x) ∑k≥0 ((2 | k))(x2)k
= [((2|0)) + ((2|1))x2 + ((2|2))x4 + ...] + [((2|0))x + ((2|1))x3 + ((2|2))x5 + ...]
Thus a2j = a2j+1 = ((2 | j)) = j+1.
3c. Use (1+x+x2)(1−x) = 1−x3 to massage the denominator into the form 1 / (1−x3)2. Then use the known series formula: 1 / (1−z)2 = ∑k≥0 ((2 | k))zk, with z = x3.
= (1+x+x2) / (1−x3)2 = (1+x+x2) ∑k≥0 ((2 | k))(x3)k
= [((2|0)) + ((2|1))x3 + ((2|2))x6 + ...] + [((2|0))x + ((2|1))x4 + ((2|2))x7 + ...] + [((2|0))x2 + ((2|1))x5 + ((2|2))x8 + ...]
Thus a3j = a3j+1 = a3j+2 = ((2 | j)) = j+1.
4a. Step 1: (choose a handful of change of any value) ⇔ (0P or 1P or ...) and (0N or 1N or ...)
is translated algebraically as:
4b. A handful of pennies and nickels worth k = 5j cents is determined by how many nickels: either 0 or 1 or ... or j−1 or j nickels, making j+1 choices. Thus N5j = j+1. Similarly for k = 5j+1, etc.
5a. (Roll two dice) ⇔ (1 OR 2 OR ... OR 6) AND (1 OR 2 OR ... OR 6). Translating into algebra: f(x) = (x + x2 + ... + x6)2. Typing this into Wolfram Alpha as: "expand (x+x^2+x^3+x^4+x^5+x^6)^2", we get:
5b. Regardless of their labels, each of the dice can land on any of their 6 faces, making 62 = 36 equally likely cases. Let sk be the number of ways to roll a total of k with Sichermann dice. For example, s3 = 2, which can appear as either of the 2's on the first die, and 1 on the second die. Using similar reasoning as before, the generating function is:
5c. Similar to part (a):
= x3+3x4+6x5+10x6+15x7+21x8+25x9+27x10+27x11+25x12+21x13+15x14+10x15+6x16+3x17+x18.
5d. f(x) = x3 (1−x6)3 / (1−x)3
=
(x3 − 3x9 + 3x15 − x21) × ∑j≥0 ((3 | j)) xj.
Multiplying out and collecting xk terms, we get:
It is not clear why this is zero for k > 18, but we may simplify using ((3 | k)) = (k+3−1 | k) = (k+2 | 2) to check that:
| a19 | = | ((3 | 16)) − 3((3 | 10)) + 3((3 | 4)) − 3((3 | −3)) |
| = | (18 | 2) − 3(12 | 2) + 3(6 | 2) − 0 = 153 − 198 + 45 = 0 . |
Notes:
- We say a sequence a0, a1, a2,... is defined recursively if we start with a given base value a0, and define each successive ak in terms of the previous ak−1, ak−2,... We wish to solve the recurrence equation, that is to give an explicit, non-recursive formula for ak.
- Example: a0 = 3 and ak = 2ak−1. This case is easy to solve: ak = 3(2k) for k ≥ 0, an exponential sequence.
- Most recurrences are much harder to solve. The Generating Function Method will often work, with some new techniques in each step.
- Step 1: Use the recurrence for ak to write an equation involving f(x) = ∑k≥0 akxk, then solve the equation to get a simple formula for f(x). Be careful with the first term a0, where the recurrence does not hold.
- Step 2: Use the partial fraction expansion of f(x) into geometric series to explicitly find its Taylor coefficients, and therefore get a formula for ak.
- Partial fraction decomposition is a technique to find the series of a rational function. A typical example is below.
- Let f(x) = (x−5)⁄(2x2+x−1). Find the vertical asymptotes, which are the roots of the denominator.
- Find the two simple functions 1⁄(1−γx) and
1⁄(1−δx)
which have the same vertical asymptotes as f(x).
Write f(x) = g(x)⁄(1−γx)(1−δx) for an appropriate numerator g(x).
Hint: For a given γ, find the asymptote of 1⁄(1−γx). Now, for our given vertical asymptotes x = −1, x = ½, what are the values γ, δ that produce these asymptotes? The polynomial (1−γx)(1−δx) has the same roots as 2x2+x−1, so the two differ only by a constant factor, which can be absorbed into the numerator g(x). - We want to find constants A,B such that
f(x) = (−x+5)⁄(1+x)(1−2x) = A⁄(1+x) + B⁄(1−2x). To do this, we combine terms on the right hand side:(−x+5)⁄(1+x)(1−2x) = (A(1−2x) + B(1+x))⁄(1−x−2x2) ; then multiply out:−x+5 = A(1−2x) + B(1+x) for all x. Now substitute any values of x, for example: x = −1 and x = ½, and solve the resulting equations for A, B. - For the A,B you found in part (c), combine terms in A⁄(1+x) + B⁄(1−2x) and verify that it is indeed f(x).
- Write out the geometric series for A⁄(1+x) and B⁄(1−2x) , and find the explicit Taylor series of f(x).
- Solving recurrences
- Base value a0 = 1, recurrence ak = 2ak−1 + 1 for k ≥ 1.
- Base value a0 = 3, recurrence ak = 3ak−1 − 2k for k ≥ 1.
- Solving general recurrences. Use generating functions to solve each of the following recurrence equations, which involve some given constants
b,c,r, and also any given base value a0. Each recurrence is valid for k ≥ 1.
(a) ak = ak−1 + c (b) ak = b ak−1 + c rk (c) ak = b ak−1 + c k
Hints: For (a), the solution ak = a0 + ck is obvious, but I want you to see what it means in terms of generating functions.
For (b), use the same reasoning as in #2a, which is the special case b = 2, c = 1, r = 1; or in #2b, which is the special case b = 3, c = −1, r = 2. Test some more examples by taking specific b,c,r,a0, computing a few terms of the series by hand, and seeing that they agree with the general formulas.
For (c), you will need the know the formula for ∑k≥0 k xk, which you can get from differentiating both sides of the geometric series formula, or from adapting the known series 1/(1−x)2. - The Golden Ratio ψ is a special number which supposedly gives the most beautiful proportions for a rectangle. It is defined by the following property: if we divide a rod of length 1 into parts ψ and 1−ψ, then the ratio of ψ to the whole length 1 is equal to the ratio of the other part 1−ψ to ψ. That is: ψ/1 = (1−ψ)/ψ .
- Solve this equation for ψ. Also compute φ = 1/ψ, and rationalize the denominator. Either ψ or φ can be called the Golden Ratio. Give decimal approximations for ψ, φ. Note: Greek letter ψ is psi, and φ is phi.
- Show that: φψ = 1, φ + ψ = √5 , and φ − ψ = 1.
- Write the roots of the polynomial 1−x−x2 in terms of ψ and φ.
1c,d. Substituting x = −1 gives 1+5 = A(1 + 2), so A = 2; and substituting x = ½ gives −½ + 5 = B(3⁄2), so B = 3. We may check that f(x) = 2⁄(1+x) + 3⁄(1−2x) by putting over a common denominator and comparing with the previous form of f(x).
1e. f(x) = ∑k≥0 2(−x)k + ∑k≥0 3(2x)k = ∑k≥0 [2(−1)k + 3(2k)] xk, so ak = 2(−1)k + 3(2k)
2a. See class notes, where I solved a similar recurrence.
Step 1: f(x) = a0 + ∑k≥1 akxk = 1 + ∑k≥1 (2ak−1+1)xk
Notice that the summation is for k ≥ 1 since the recurrence is not valid for the k = 0 term a0. Continuing:
Notice that the last summation is almost a geometric series, but with the k = 0 term missing, which accounts for the −1 at the end.
We have: f(x) = 2x f(x) + 1/(1−x), which we solve to get:
(1−2x) f(x) = 1/(1−x) and finally:
f(x) = 1/(1−x)(1−2x).
Step 2: By partial fraction decomposition,
Check: This agrees with the first few values a0 = 1, a1 = 3, a2 = 7, a3 = 15.
2b. Step 1: f(x) = a0 + ∑k≥1 akxk = 3 + ∑k≥1 (3ak−1−2k)xk
The summation is for k ≥ 1 since the recurrence is not valid for the k = 0 term.
f(x) = 3 + 3x ∑k≥1ak−1xk−1 − ∑k≥12kxk = 3 + 3x f(x) − 1/(1−2x) + 1.
The final +1 is because the geometric series ∑k≥12kxk
is missing its k = 0 term.
We have: f(x) = 3x f(x) − 1/(1−2x) + 4 = 3x f(x) + (3−8x)/(1−2x), which we solve to get: f(x) = (3−8x) / (1−2x)(1−3x).
Step 2: By partial fraction decomposition,
Check: This agrees with the first few values a0 = 3, a1 = 7, a2 = 17, a3 = 43.
3a. Recurrence: ak = ak−1 + c. We do this by generating functions just for practice.
=
a0 + x ∑k≥1 ak−1xk−1 + cx ∑k≥1 xk−1
= a0 + x f(x) + cx/(1−x)
= a0 + a0x + c((2|0))x + a0x2 + c((2|1))x2 + ...
3b. Recurrence: ak = b ak−1+ c rk. Here the answer is not at all obvious. Step 1 gives:
f(x) = a0 + bx f(x) + crx/(1−rx) so f(x) = a0/(1−bx) + crx/(1−rx)(1−bx)
Partial fractions: crx/(1−rx)(1−bx) = A/(1−rx) + B/(1−bx) .
Clear denominators, substitute x = 1/b, 1/r , get A = cr/(r−b), B = −cr/(r−b).
Final answer: ak = a0bk + A rk + B bk = a0bk + cr(rk − bk)/(r−b).
Check: For the case in Prob #2, we have b = 2, c = r = 1, a0 = 1, so ak = 1(2k) + 1(1k−2k)/(1−2)
= 2k − (1−2k) = −1 + 2k+1 as we got in #2.
3c. Recurrence: ak = b ak−1 + ck . This one is harder than I would give on a test.
First, differentiating (1−x)−1 = ∑k≥0 xk gives: (1−x)−2 = ∑k≥0 kxk−1,
so x/(1−x)2 = ∑k≥0 kxk.
Equation: f(x) = a0 + bx f(x) + cx/(1−x)2 so f(x) = a0/(1−bx) + cx/(1−bx)(1−x)2
Partial fractions: cx/(1−bx)(1−x)2 = A/(1−bx) + B/(1−x)2 + C/(1−x) .
Clear denominators and substitute x = 1/b, x = 1 to get A = cb/(b−1)2 , B = −c/(b−1) .
Then we have: C/(1−x) = cx/(1−bx)(1−x)2 − A/(1−bx) − B/(1−x)2 = −c/(b−1)2(1−x) .
Final answer: ak = (a0 + cb/(b−1)2) bk − ck/(b−1) − cb/(b−1)2 .
Check: Compare with obvious formulas in the case b = 0 and in the case c = 0 .
4a. The equation reduces to ψ2 = 1−ψ, or ψ2+ψ−1 = 0, which has roots (−1±√5)/2. The positive root is ψ = (√5−1)/2 .
Also φ = 1/ψ = 2/(√5−1) = 2(√5+1) / (√5−1)(√5+1) = 2(√5+1) / (5−1) = (√5+1) / 2. The approximate values are ψ ≅ 0.6 , φ ≅ 1.6 .
4b. The roots are ψ and −φ.
Notes: We defined the Fibonacci numbers by the initial values F0 = 0, F1 = 1, and the recurrence:
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 |
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
We computed the generating function as follows:
| f(x) | = | F0 + F1x + ∑k≥2 Fkxk |
| = | x + ∑k≥2 (Fk−1 + Fk−2)xk | |
| = | x + x ∑k≥2 Fk−1xk−1 + x2 ∑k≥2 Fk−2xk−2 | |
| = | x + x (F1x + F2x2 + F2x3 + ...) + x2 (F0 + F1x + F2x2 + ...) | |
| = | x + x (f(x) − F0) + x2 f(x) | |
| f(x) | = | x + x f(x) + x2 f(x) |
Fk = (φk − (−ψ)k ) / √5 ,
where the constants are the two reciprocal values of the Golden Ratio (see HW 2/10 #4):
HW:
- Explain the mistakes in each of the following computations.
- ∑k≥0 3kxk = 3k ∑k≥0 xk = 3k / (1−x). Hint: Focus on the meaning of "k".
- 1⁄(1−3x) − 1⁄(1−2x) = ∑k≥0 3xk − ∑k≥0 2xk = ∑k≥0 (3−2)xk = ∑k≥0 xk.
- If a0 = 1 and ak = 2ak−1 + 1 for k ≥ 1, then:
f(x) = ∑k≥0 akxk = a0 + ∑k≥1 (2ak−1+1)xk = 1 + ∑k≥1 2xk + ∑k≥1 xk = 1 + x⁄(1−2x) + x⁄(1−x)
- Practice:
Solve the following recurrence using the Generating Function Method.
a0 = a1 = 1, a2 = 2, ak = 3ak−1− 3ak−2+ ak−3 for k ≥ 3 . - Step 2 for the Fibonacci sequence. Show that the asymptotes of the Fibonacci f(x) = x / (1−x−x2) are x = −φ and x = ψ, and repeat the analysis in HW 9/27 #2. Determine the partial fraction decomposition f(x) = A/(1−ax) + B/(1−bx), and find the explicit Taylor series of f(x), which gives Binet's formula.
Hint: In your calculations, use that φ = 1/ψ , φ+ψ = √5 , and φ−ψ = 1. - Binet formula for Fibonacci numbers.
- In this formula, the irrational square roots somehow cancel, leaving only whole numbers, the Fk's. Check Binet's formula by hand for k = 0, 1, 2, 3.
- Since |ψ| < 1, its powers become very small, so that the second term in the above formula is only a small correction. In fact:
Fk = round(φk / √5), where round( ) means round to the nearest integer. This confirms the intuition that Fk should grow exponentially, since it is a model of (delayed) reproduction.
Problem: On your calculator, compute φk / √5 for k = 1,2,...,12. How close are they to the Fibonacci numbers? Do you have to round up or down? Explain the direction of the rounding by looking at the original formula. - Use the rounding formula and your calculator to compute F40 exactly. Give a general formula for the number of digits in the number Fk.
- Extra Credit: Arithmetic properties of Fk.
- For which k is Fk an even number? Prove your answer by induction, but be careful, since the result of the next step is not necessarily the same as the previous step.
- Prove that if nk is a multiple of k, then Fnk is a multiple of Fk .
- Extra Credit: Fk in terms of binomial coefficients. If we use different algebraic tricks on the generating function of the Fibonacci numbers, we get another formula for Fk.
Factoring out an x from the generating function, we get:f(x)/x = ∑k≥0 Fk+1 xk = 1 / (1 − (x+x2)) . Expand this in two stages. First use the geometric series formula 1/(1−z) = ∑j≥0 zj with z = x+x2 . Then expand (x+x2)j by the Binomial Theorem. You should get a double sum of the form:f(x)/x = ∑ j≥0 ∑ji=0 .... You may prefer to write this out in a table of terms with rows corresponding to j = 0, 1, 2,... and columns corresponding to i = 0, 1,..., j.
Now collect terms with like powers of x : that is, add up the coefficients with no x, with x1, x2, x3, until you see the pattern. Or use summation notation, and collect the terms corresponding to all values of j and i which produce a total exponent equal to k. Obtain a formula for Fk as a sum of certain choose numbers (j | i). Write your formula explicitly for k = 1,...,6 . - Extra Credit: A counting model for Fk. A hopscotch board is a sequence of columns, each with 1 or 2 squares (see picture HHM p.181 #10). Let hk be the number of boards with a total of k squares. Equivalently, hk is the number of ways of splitting k into a sum of 1's and 2's, where order matters. For example, h5 = 8 counts the 8 sums:
5 = 2+1+1+1 = 1+2+1+1 = 1+1+2+1 = 1+1+1+2 Also let h0 = 1.
= 2+2+1 = 2+1+2 = 1+2+2 = 1+1+1+1+1 .
Find the generating function of hk using the Sum and Product Principles. Choosing any sum of 1's and 2's is equivalent to the following: first decide how many 1-or-2 numbers you will add (say, j numbers), then choose 1 or 2 for each of the j numbers. This choice will contribute to hk where k is the sum of the 1-or-2 numbers chosen. Sum over all j ≥ 0 to get the generating function of hk's . You should get a kind of geometric series 1 + z + z2 + ... , which you can sum using the usual formula. Now use the result to compare hk to the Fibonacci numbers.
The letter "k" is a dummy variable that takes on a particular value k = 0,1,2,... in each successive term of the summation ∑k . It has no meaning outside the summation, and the correct final formula has no k variable in it.
1b. We should write: 1⁄(1−3x) = ∑k≥0 (3x)k = ∑k≥0 3kxk, and similarly for 1⁄(1−2x) , giving total coefficient ak = 3k − 2k.
1c. After the third equals sign, the ak just disappeared from the expression, which is wrong since in general ak ≠ 1. After the fourth equals sign, the expression 2xk was confused with as (2x)k, as in part (b).
2. Step 1:
| f(x) | = | a0 + a1x + a2x2 + ∑k≥3 akxk |
| = | 1 + x + 2x2 + ∑k≥3 (3ak−1− 3ak−2+ ak−3)xk | |
| = | 1 + x + 2x2 + 3x ∑k≥3 ak−1xk−1 − 3x2 ∑k≥3 ak−2xk−2 + x3 ∑k≥3 ak−3xk−3 | |
| = | 1 + x + 2x2 + 3x (a2x2 + a3x3 + ...) − 3x2 (a1x + a2x2 + ...) + x3 (a0 + a1x + ...) | |
| = | 1 + x + 2x2 + 3x (f(x) − a0 − a1x) − 3x2 (f(x) − a0) + x3 f(x) | |
| = | 1 + x + 2x2 + 3x f(x) − 3x − 3x2 − 3x2 f(x) + 3x2 + x3 f(x) | |
| f(x) | = | 1 − 2x + 2x2 + 3x f(x) − 3x2 f(x) + x3 f(x) |
| f(x) | = | (1 − 2x + 2x2) ∑k≥0 ((3 | k))xk | |||||||||||||||
| = |
|
3. The simple functions with the asymptotes x = ψ and x = −φ are 1/(1 − x/ψ) = 1/(1−φx) and 1/(1 + x/φ) = 1/(1+ψx), since 1/ψ = φ and 1/φ = ψ.
In fact 1 − x − x2 = (1−φx)(1+ψx), since the two sides are polynoimals with the same roots and the same constant term.
Multiplying out x / (1−x−x2) = A/(1−φx) + B/(1+ψx), we get x = A(1+ψx) + B(1−φx) for all x.
Substituting x = ψ gives ψ = A(1+ψ2) + B(1−φψ) = A(1+ψ2) so A = ψ/(1+ψ2) = ... = 1/√5.
Similarly B = −1/√5.
It is much easier to rewrite the original equation as: x = (A+B) + (Aψ−Bφ)x,
and equate the constant terms and the coefficients of x on the two sides: 0 = A+B, so that B = −A; and
1 = Aψ−Bφ = Aψ+Aφ, so that A = 1/(ψ+φ) = 1/√5 and B = −1/√5.
4a. For example:
| F3 | = | [(1+√5)3 − (1−√5)3] / 23√5 |
| = | [ (1 + 3√5 + 3√25 + √125) − (1 − 3√5 + 3√25 − √125)] / 8√5 | |
| = | (6√5 + 2(5)√5) / 8√5 = 16 / 8 = 2 (!?) |
4b. You round down when k is even and the correction term −(−ψ)k is negative, and round up when k is odd and −(−ψ)k is positive.
4c. F40 = round( (1.618033988749895)40 / 2.2360679774997896 )
= round( 1.023341550000000019 × 108 )
= 102334155 .
The run of 0's in the decimal expansion is because the correction term −(−ψ)k / √5 is exponentially small.
The number of digits is the rounding-down of:
HW: Consider the generating function
This is the most essential way to encode the numbers ak: all the other forms follow from it.
- Use Wolfram Alpha to find the first few Taylor coefficients ak.
- Expand the left side of the equation (1−2x−x2) ∑k≥0 ak xk = 1, and equate the xk coefficients on the two sides. (The right side is 1 = 1 + 0x + 0x2 + ....). Use this to find a recurrence equation for ak, and verify that it works for the values from Prob 1.
- Find the roots x = α, β of the denominator, solving 1−2x−x2 = 0.
Use this to factor:
1 − 2x − x2 = −(x−α)(x−β) = −αβ(1 − x⁄α)(1 − x⁄β). = (1−ax)(1−bx).
(Remember to rationalize the denominator.) Find the partial fraction decomposition of f(x), and expand the corresponding geometric series to find an explicit formula ak = A ak + B bk. - Find an approximate formula: ak ≈ A ak coming from the larger term in the explicit formula from Prob 3. How accurate is this approximation?
- Expand f(x) as:
f(x) = 1⁄(1 − (2x+x2)) = ∑n≥0 (2x + x2)n,
and translate this algebraic expression into a logical choice algorithm. That is, find a class of combinatorial objects such that ak couunts the objects of size k.
Hint: 2x + x2 = x + x + x2 can be interpreted as two basic options of size 1 (a red one and black one), and one basic option of size 2.
3. ak = (ak+1 + (−1)kbk+1)⁄2√2 , where a = 1+√2, b = −1+√2.
5. Suppose we have a balance scale with an unlimited supply of three kinds of weights: red 1oz, black 1oz, and 2oz. Then ak is the number of ways to balance k oz with an ordered row of weights.
Notes:
- We defined the Catalan numbers by thinking of a game in which you start with $1, and win or lose $1 in each round. A game lasts 2k rounds (an even number), and we impose the restricitons:
- You break even, having $1 at the end of the 2k rounds (k wins, k losses).
- You never go bankrupt (get to $0).
- We can picture such games by Catalan paths (also called Dyck paths), which depict the graph of winnings after each round. These look like zigzag paths in the plane
starting at (0,1), meaning $1 at round 0, ending at (2k, 1), meaning back to $1 after 2k rounds, and going up or down by 1 with each step to the right. Never going bankrupt means the graph must stay on or above the baseline y = 1, and never touch the x-axis. The two paths of C2 are:
- The Ck's can be computed recursively starting with C0 = 1, using the formula:
Ck = C0Ck−1 + C1Ck−2 + C2Ck−3 + ... + Ck−1C0 for k ≥ 1
and C0 = 1. For example: C3 = C0C2 + C1C1 + C2C0 = (1)(2) + (1)(1) + (2)(1) = 5.
This formula can be proved by a transformation which breaks any Ck path into a unique pair of a Cm−1 path and a Ck−m path, where 1 ≤ m ≤ k.- Divide the path at the first point where it returns to the baseline, so there are 2m steps left of the division point and 2k−2m steps to the right.
- The left part starts with a + and ends with a −, and the part in between is a Cm−1 path never going below the line y = 2. (I described this in class as the part of the path "on stilts".)
- The right part is a Ck−m path.
- This tranformation has an obvious inverse, taking a pair of paths in Cm−1 × Cm−k, for 1 ≤ m ≤ k, to a path in Ck. This it is one-to-one and onto, giving the recurrence equation.
- Example: The C4 path (+ + − − + − + −) first returns to the baseline after 2m = 4 steps, so we can split it into left, stilt, and right parts as:
(+ + − − + − + −). That is, the left part (without the stilts) is the C1 path (+ −); and the right part is the C2 path (+ − + −).
Every C4 path can be split into a pair of C0×C3 , C1×C2 , C2×C1 , or C3×C0 paths.
HW:
- Draw all the paths for C3 = 5 and C4 = 14. For each path, identify its left and right parts (of length 2m−2 and 2k−2m) according to the rule in the Notes above. Observe that all pairs of paths occur, illustrating the recurrence equation.
- Use the recurrence equation to algebraically compute C1,... C10. Can you find any patterns, or guess any formula? Which Ck's are odd versus even?
- Grouping products: one of the many, many problems that give rise to Catalan numbers.
The associative law says that a product does not depend on the grouping of factors: for example 2×3×4 can be multiplied as (2×3)×4 = 6×4 = 24 and 2×(3×4) = 2×12 = 24. Abstractly:(x0x1)x2 = x0(x1x2). Of course it works with more factors, and there are more ways to multiply:((x0x1)x2)x3 = (x0(x1x2))x3 = (x0x1)(x2x3) = x0((x1x2)x3) = x0(x1(x2x3)) Let Mk be the number of ways to group k+1 factors x0x1...xk , so that M0 = M1 = 1, M2 = 2, M3 = 5.- Find a recurrence for Mk as follows. Sort the Mk groupings into cases, depending on where the outermost (last) multiplication occurs.
For example, in (x0x1)(x2x3), the last-multiplication division point is after x1, and the number of groupings with this division point is M1M1 = 1.
In ((x0x1)x2)x3 and (x0(x1x2))x3, the division point is between x2 and x3, and the number of groupings with this division point is M2M0 = 2. - Prove by induction that Mk = Ck . This is obvious since....
- Find a recurrence for Mk as follows. Sort the Mk groupings into cases, depending on where the outermost (last) multiplication occurs.
- A family tree (ordered tree) is a structure of unlabeled vertices or nodes connected by edges as follows. At the top is one node (the ancestor), with some number of nodes coming down from it (indicating children), listed in age order left-to-right. Then each of these has some nodes coming down from it, etc., eventually ending in nodes without children. The family trees (ordered trees) with 4 nodes are:
Note that the difference between the 3rd and 4th trees is whether the ancestor's older or younger child has his own child.
Let Ok be the number of ordered trees with k nodes, so that O1 = O2 = 1, O3 = 2, O4 = 5.
Problem: Find a recurrence for Ok by splitting a tree into the subtree coming from the ancestor's oldest child, and the other subtree with everyone else. Compute some values of Ok and compare to Ck. Prove your comparison. - Compute the Taylor series of √(1−x) = (1−x)1/2. Hint: Use Taylor's Formula for the coefficients, just as for the Binomial Theorem with negative exponents.
- Extra Credit: HHM Ch 2.6.6, p.190 #6. Suppose 2k people are seated around a table. How many ways are there for k pairs to shake hands simultaneously across the table in such a way that no arms cross? Geometrically: mark 2k nodes on a circle, and pair the nodes up by drawing curves between them, so that no two curves cross. Let Hk be the number of handshake-patterns for 2k people.
For example, H3 = 5 counts the following patterns:
Find H4 by drawing out all possible patterns for 8 nodes. Guess a relation of Hk to Ck. Prove a Catalan-like recurrence for Hk, which gives a recursive algorithm for drawing patterns, and also proves the relation between Hk and Ck. Finally, find a simple, explicit transformation between handshake patterns for 2k people and parentheses for grouping the product x0...xk, as in #3 above: this directly proves that Hk = Mk, which we know is Ck.
Hint: Given a handshake pattern, saw the table in half along the curve starting at the top node, getting left and right pieces of the table, which can be considered as smaller tables with nodes (guests) around them. Fixing the number of nodes in each piece, how many smaller handshake patterns can be inserted? Sum these to get the recurrence.
For C3, we show the left part (on stilts) and right part of each path:
2.
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Ck | 1 | 1 | 2 | 5 | 14 | 42 | 132 | 429 | 1430 | 4862 | 16796 |
3a. The groupings with division point after xm split into a factor with m+1 variables and one with k−m variables, with 0 ≤ m ≤ k−1; considering recursively, there are MmMk−m−1 such groupings. Thus Mk = M0Mk−1 + M1Mk−2 + ... + Mk−1M0.
3b. Mk and Ck are computed using exactly the same recursion, starting from the same initial value M0 = C0 = 1, so they must be equal.
Formally, we can prove it by induction. Mk = Ck is definitely true for k = 0. Now assume it is proved up to a given k. Then
Mk+1 = MkM0 + Mk−1M1 + ... + M0Mk. By assumption M0 = C0, M1 = C1,..., Mk = Ck, so the right hand side equals
CkC0 + Ck−1C1 + ... + C0Ck, which equals Ck+1 by the known recurrence. Thus the equality Mk+1 = Ck+1 also holds, and the induction proceeds. Conclusion: Mk = Ck holds for all k ≥ 0.
4. Any tree T with k ≥ 2 splits into two subtrees: T' coming from the ancestor's oldest child (having m ≥ 1 vertices), and T'' with everyone else, including the ancestor (having k − m vertices). Conversely, any T' and T'' can be put together in a unique way to get a T (i.e. make the ancestor of T' into the oldest child of the ancestor of T''). Considering recursively, the number of pairs (T' , T'') is OmOk−m.
Thus, Ok = Ok−1O1 + Ok−2O2 + ... + O1Ok−1. This is the same recurrence as for the sequence C'k = Ck+1 , so Ok = C'k = Ck+1.
In the picture above, the first two trees are of type O3O1, since the subtree T' coming from the oldest (only) child has 3 vertices, and the rest make a tree T'' with 1 vertex (the ancestor alone).
The third tree is of type O2O2, since the subtree T' from the oldest child has 2 vertices, and the rest make T'' with 2 vertices. The last two trees are of type O1O3, since the oldest child has no children, and there are 3 vertices besides.
5. The kth derivative of (1−x)1/2 is (−1)k(½)(½−1)(½−2)...(½−k+1)(1−x)1/2 − k, so the kth coefficient of the Taylor series is ak = (−1)k(½)k / k!. This can be rewritten as:
= −( 1(3)(5)...(2k−3) / 2kk! ) ( 2(4)(6)...(2k−2) / 2k−1(k−1)! )
= −(2k−2)! / (k−1)!(k−1)!22k−1k = −(2k−2 | k−1) / 22k−1k
HW:
- The explicit formula for Catalan numbers is:
Ck = 1⁄(k+1) (2k | k) = (2k)!⁄k!(k+1)! - Compute C0,... C8 using the formula. Does it give the correct answers, comparing with HW 2/17 #2 ?
- The Catalan number Ck counts Catalan paths (also called Dyck paths):
paths in the plane from (0,1) to (2k,1), never going below y = 1, and having 2k steps, each going right by +1, and up-or-down by ±1.
Problem: Why would you think of (2k | k) in relation to counting paths? There is a fairly natural relation, though it does not explain full formula for Ck . - Extra Credit: The Formula looks like a fraction, not a whole number: it seems a "coincidence" that (2k | k) is always divisible by k+1. Can you give an algebraic or combinatorial reason for this?
- Recall that the Catalan generating function is f(x) = ∑k≥0 Ckxk = (1 − √(1−4x)) / 2x .
Go through Step 2 of the Method for the modified function:
h(x) = xf(x) = C0x + C1x2 + C2x3 + ... = ½ − ½√(1−4x). You can find the Taylor series h(x) = ∑k≥0 akxk directly from Taylor's formula ak = h(k)(0) / k!, or use the result of HW 2/17 #5. Conclude by computing Ck = ak+1, and obtaining the Formula above. - Recall that we used the Reflection Principle to show that:
Ck = (2k | k) − (2k | k−1).
That is, we took the large set of all 2k-step up/down paths from (0,1) to (2k,1): choosing such a path is the same as choosing the positions of the k up-steps, so there are (2k | k) paths in total. Among these paths are the Ck Catalan paths which never dip below the baseline y = 1; and also the bad paths which touch or cross the x-axis. Now we transform these bad paths by vertically reflecting the part after they first touch the x-axis, obtaining a 2k-step path from (0,1) to (2k,−1). Here are two examples of the Reflection Transformation for k = 4:
This transformation is reversible, so that any 2k-step path from (0,1) to (2k,−1) can be reflected back to a path from (0,1) to (2k,1). Choosing a path on the right corresponds to choosing the positions of the k−1 up-steps, so there are (2k | k−1) such paths, and the same number of bad paths on the left. That is, the number of good paths is Ck = (2k | k) − (2k | k−1).- Show algebraically that (2k | k) − (2k | k−1) = 1⁄(k+1) (2k | k), which recovers our previous formula for Ck .
- Illustrate the proof that C3 = (6 | 3) − (6 | 2) = 20 − 15, by drawing a diagram of the Reflection Transformation. Make a list of the (6 | 3) up/down paths from (0,1) to (6,1), including the Catalan paths (also called Dyck paths) which do not dip below the baseline y = 1, and the bad paths which touch or cross the x-axis. For each bad path, draw its reflected path in a new column: that is, vertically reflect the portion after the first touch of the x-axis, obtaining a new up/down path from (0,1) to (6,−1). Check that the reflected paths include all (6 | 2) up/down paths from (0,1) to (6,−1): this shows the nuumber of bad paths in the first column is also (6 | 2).
2. h(x) = ½ − ½(1−4x)1/2 , h'(x) = (1−4x)−1/2 , h''(x) = ½(4)(1−4x)−3/2 , h'''(x) = (1⁄2)(3⁄2)(42)(1−4x)−5/2, and:
| ak = h(k)(0) / k! | = (1⁄2)(3⁄2)...(2k−3⁄2) 4k−1 / k! |
| = (1)(3)(5)...(2k−3) 4k−1 / 2k−1 k! | |
| = (1)(3)(5)...(2k−3) 2k−1(k−1)! / (k−1)! k! | |
| = (1)(3)(5)...(2k−3) (2)(4)(6)...(2k−2) / (k−1)! k! | |
| = (2k−2)! / (k−1)! k! = 1⁄k (2k−2 | k−1) . |
3a. By the Reflection Principle, we have Ck = (2k | k) − (2k | k−1), which simplifies algebraically as:
= (2k)!⁄k!(k−1)! (1⁄k(k+1)) = 1⁄(k+1) (2k)!⁄k!k! = 1⁄(k+1) (2k | k).
3b.
Notes: In this HW, we examine a simpler example of symmetry.
-
Let X be a rectangle (not a square) with vertices (corners) labeled for reference:
1 −−−−−− 2 | | 4 −−−−−− 3 - A symmetry of X is a mapping (or function) σ : X → X taking each point of X to another point of X, in a way that preserves the structure (in this case the geometric structure of distances and angles). For example, the side-to-side reflection τ1 mirrors each point across the vertical central line of X, mapping the corners as:
τ1(1) = 2,
τ1(2) = 1,
τ1(3) = 4,
τ1(4) = 3.
This preserves the structure, because the distance between 1 & 4 (the short side of the rectangle) is the same as the distance between τ1(1) & τ1(4), i.e. between 2 & 3; and similarly for every pair of points on X. - We call the set of all symmetries of X the symmetry group G = Sym(X).
- Each symmetry is a function σ : X → X, and each vertex i is taken to some vertex σ(i) = j.
We represent each symmetry by a two-line table with the input vertices 1,2,3,4 on the top line, and on the bottom line their symmetric images, the output vertices σ(1), σ(2), σ(3), σ(4) .
Example: τ1 is represented by the two-line notation: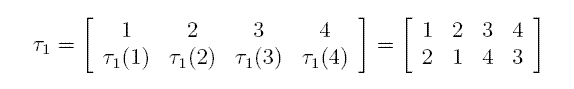
- The trivial symmetry is the identity mapping ε : X → X, which takes each point to itself: ε(1) = 1, ε(2) = 2, etc. so that:
- The symmetric group Sn be the set of all possible mappings σ : [n] → [n] which take the set [n] = {1,2,...,n} one-to-one onto itself. This is the symmetry group of the set [n] thought of as a handful of identical marbles, which can be switched around arbitrarily. Since the one-line notation for σ is just an ordering of [n], there are |Sn| = n! such mappings.
- By representing each symmetry of the rectangle X in terms of how it switches the corners, we find G = Sym(X) ⊂ S4; that is, G is a subgroup of S4 .
- Greek letters: α alpha, β beta, γ gamma, ε epsilon, ρ rho, σ sigma, τ tau.
- List the all the geometric symmetries of the rectangle X, including the identity ε, rotations ρ1, ρ2, ... and reflections τ1, τ2 .... For each symmetry σ, draw the rectangle and an arrow from each vertex i to the vertex σ(i) that it is mapped to (its image vertex).
Hints:- The 1⁄4 turn is not a symmetry, since it does not take the rectangle onto itself; rather, it would stand the rectangle on end.
- To make sure you have found all the symmetries, consider a general symmetry σ, and count the possibilities for σ(1), then the remaining possibilities for σ(2), etc. This will give an upper bound for the number of symmetries.
- Write the two-line table for each symmetry σ. That is, put the vertex-labels 1,2,3,4 on the top line, and their symmetric images σ(1), σ(2), σ(3), σ(4) on the bottom line, as in the examples above.
- For each pair of symmetries α, β, consider the composition α ∘ β, meaning do α after β, giving another symmetry γ. Picture this γ and identify it as one of the known symmetries.
Also try computing α ∘ β symbolically, by seeing where it takes each vertex i: first β takes i to some j = β(i), then α takes this image point to α(j), so γ(i) = α(β(i)). The table of γ can then be identified as one of the known two-line tables from #2.
Record the results in a multiplication table, with rows and columns labeled by id, ρ, τ1, τ2; and in row α and column β, write the letter of the symmetry γ = α ∘ β .
Example: To compute τ1 ∘ τ1, we can picture that two reflections bring every point back to itself, so τ1 ∘ τ1 = ε. Or we can compute that τ1(τ1(1)) = τ1(2) = 1 and similarly τ1(τ1(i)) = i. But this is the same function as the identity ε(i) = i, so τ1 ∘ τ1 = ε. Thus in the multiplication table, in the diagonal position with row τ1 and column τ1, we write ε.° ε ρ τ1 τ2 ε ρ τ1 ε τ2 - Recall that each symmetry σ can be undone by its inverse symmetry σ−1, so that σ−1 ∘ σ = ε.
- For each of our σ ∈ G, find σ−1.
- Given σ ∈ Sn, how to find σ−1? For example, what is [4,2,5,3,1]−1 ?
- We say a group G is commutative if σ ∘ τ = τ ∘ σ for all σ, τ ∈ G.
- Is our G = Sym(X) commutative? How can you check from the multiplication table?
- Find σ, τ ∈ S3 which do not commute. Use this to show that Sn is never commutative for n ≥ 3.
For an arbitrary symmetry σ, vertex 1 must go to one of the vertices σ(1) = 1,2,3, or 4; and this forces σ(2) to be the long-edge neighbor of σ(1); and there is also only one choice for σ(3), σ(4). Thus there are at most 4 symmetries, and we have found them all.
2. The two-line tables for the symmetries are:
|
|
|
3. With a little practice, you can easily multiply using two- or one-line notation. For example:
since: ρ(τ1(1)) = ρ(2) = 4; ρ(τ1(2)) = ρ(1) = 3; ρ(τ1(3)) = ρ(4) = 2; ρ(τ1(4)) = ρ(3) = 1. The multiplication table is:
| ° | ε | ρ | τ1 | τ2 | |||||||||||||||
| ε | ε | ρ | τ1 | τ2
| ρ | ρ | ε | τ2 | τ1
| τ1 | τ1 | τ2 | ε | ρ
| τ2 | τ2 | τ1 | ρ | ε
| |
4a. Each element is its own inverse, as we can see from ε's on the diagonal of the multiplication table. Note that in general, a symmetry is usually not its own inverse.
4b. We find σ−1 by reversing the inputs and outputs of σ. Thus, for σ = [4,2,5,3,1], we have σ(1) = 4, so σ−1(4) = 1, etc., and σ−1 = [5,2,4,1,3]. Given 2-line notation, we can switch the top and bottom lines, then rearrange the columns so as to get 1,2,...,n on top.
5a. Our group G, the symmetries of the rectangle, is a commutative group: we see that the table is symmetric across the upper-left to lower-right diagonal, so that an upper-right entry σ ∘ τ is the same as the corresponding lower-left entry τ ∘ σ.
5b. Writing in one-line notation, we have [2,1,3] ∘ [1,3,2] = [2,3,1], whereas [1,3,2] ∘ [2,1,3] = [3,1,2], so [2,1,3] and [1,3,2] do not commute. We can duplicate this in every larger Sn by just defining σ(i) = i for i ≥ 4. For example: [2,1,3,4,5] ∘ [1,3,2,4,5] = [2,3,1,4,5], etc.
HW:
- Cycle notation. Consider the permutation σ ∈ S8 given in 2-line notation by:
σ = ⌈ 1 2 3 4 5 6 7 8 ⌉ ⌊ 6 8 7 4 1 5 2 3 ⌋ - Draw σ as an arrow-diagram, with vertices 1,2,...,8 in a circle, and an arrow from each i to its image σ(i). For example, an arrow from 1 to 6, from 2 to 8, etc.
- Tracing the arrow-cycles in part (a), write σ in cycle notation. Hint: Since σ(1) = 6, σ(6) = 5, σ(5) = 1, one of the cycles is (1,6,5).
- Now draw an arrow diagram for the inverse permutation σ−1, which undoes σ. (That is, if σ(i) = j, then σ−1(j) = i.) Write its cycle notation. In general, what is the rule for the inverse of a cycle?
- The rigid symmetries (turning and flipping) of a regular n-gon form the dihedral group Dn. (In class, we looked at D3, the 6 symmetries of an equilateral triangle, and D4, the 8 symmetries of a square.)
We label the vertices clockwise 1,2,..,n, and consider each symmetry as a permutation of the vertices, meaning Dn ⊂ Sn. For example, the 1⁄n clockwise turn ρ1 is the permutation:
ρ1(1) = 2, ρ1(2) = 3, ... , ρ1(n) = 1,
which in cycle notation is (123...n). (Warning: This is quite different from the one-line notation
σ = [123...n], which means σ(1) =1, σ(2) = 2, etc., so that σ = ε.)
In general, let ρk denote a k⁄n clockwise rotation, and denote the reflections by τk for k = 1,...,n.
- For D4, write each of the 8 symmetries in two-line notation.
- For D4, show that ρk = ρ1 o ... o ρ1 = ρ1k, the composition of ρ1 with itself k times.
- For D4, show that the reflections τk are all given by τ1 o ρ1k. Thus, all the elements of D4 can be obtained by composing τ1 and ρ1: we say these two elements generate the group.
- Rotations of a cube.
Let X be a cube in space and G = Sym(X) be the group of its rotation symmetries only.
Mirror reflections are not allowed, only the symmetries obtained by moving the cube in your hands.
The easiest way to deal with this group is to consider it as permutations of the 6 faces of the cube (rather than the 8 vertices),
so that G ⊂ S6. It is helpful to picture X using dice, so that faces 1,2,3 share a corner, and each pair of opposite faces total 7 (1 is opposite 6, etc.).
- Show that |G| ≤ 24: there are at most 24 rotations of the cube (counting the identity). Hint: Think where face 1 can be moved, then faces 2,3.
- In fact, there are exactly 24 symmetries in G. To find them, consider that G is generated by the one-quarter rotations around the x, y, and z axes, which we may write as permutations in cycle notation:
α = (1)(6)(2354) , β = (2)(5)(1364) , γ = (3)(4)(1265) . That is, α takes faces 1 and 6 to themselves because the x-axis runs through these faces.
These elements and their powers account for 10 symmetries in G. For example, α2 is a one-half rotation around the x-axis.
Problem: Find the other 14 symmetries.
Hint: There are two more types of rotation symmetry, each of which can be centered around several axes. Once you can picture what these should be, just write them all down in cycle notation. - Extra Credit: The fact that |G| = 24 = 4! should make you suspect it is the "same" as S4, the group of all permutations of 4 objects. (Technically, we say the groups are isomorphic.) In fact, there is a way to picture each cube rotation as switching around 4 objects constructed inside the cube, with all 4! permutations appearing. How?
- We illustrate colorings of X in the example where X is the rectangle from HW 2/22, having vertices (corners) labeled clockwise by {1,2,3,4}:
The symmetry group G = Sym(X) contains the identity ε, the 1⁄2 rotation ρ, and horizontal and vertical reflections τ1, τ2. (The 1⁄4 rotation is not a symmetry of X because it does not move the rectangle onto itself.)1 −−−−−− 2 | | 4 −−−−−− 3
Consider ways to color the vertices with k = 2 colors (Red and Blue), that is, functions c : {1,2,3,4} → {R,B} which we can write by listing the color of each vertex: for example, BBRB means c(1) = B, c(2) = B, c(3) = R, c(4) = B. The set of all colorings (without considering symmetry) is C, with |C| = 24 = 16.- Draw all 16 colorings as rectangles with each vertex labeled with its color.
- Two colorings c and c' are equivalent up to symmetry if one can be moved to the other by some σ ∈ G = Sym(X), written c' = σ(c). (For example, we can flip the colors horizontally or vertically.)
The symmetry class of a coloring c is the set of all colorings symmetric to it: c
= {c' = σ(c) for all σ ∈ G}.
Problem: Draw the 16 colorings grouped into symmetry classes, and determine |C|, the number of distinct symmetry classes, i.e. the number of colorings "up to symmetry", counting symmetric colorings as the same. - Now let D be the colorings of the rectangle with k = 4 colors (which we can think of as stickers with
the numbers 1,2,3,4) such that each vertex has a different color.
(These are equivalent to one-to-one mappings c : [4] → [4].)
Write all of the colorings in D, grouped into symmetry classes, and determine |D|, the number of colorings in D up to symmetry.
- Now let X be the cube, and let D denote the colorings of the 6 faces by 6 different colors, thought of as stickers 1,2,...,6 (i.e. configurations of dice). Find |D|,
the number of possible configurations.
Extra Credit: Why don't all of these appear in commercial dice? What further specification do these obey? How many configurations of cubical dice are actually sold?
1c. The inverse permutation reverses each cycle, so that σ−1 = (5,6,1)(7,3,8,2)(4) = (1,5,6)(2,7,3,8)(4).
2a. We write each element of the dihedral group in cycle notation, including the abbreviated form omitting cycles of length 1. Note that an element like σ = (1432) means σ(1) = 4, σ(4) = 3, σ(3)=2, σ(2) = 1, and we could equivalently write σ = (2143) = (3214) = (4321).
τ1 = (12)(34) τ2 = (1)(24)(3) = (24) τ3 = (14)(23) τ4 = (13)(2)(4) = (13).
2b. We have ρ1(i) = i+1 modulo n. This means we wrap around an n-hour clock, with n = 0, n+1 = 1, etc. Performing this k times, we get ρ1k(i) = i+k modulo n, and this is clearly ρk(i). Note also that ρ1n = ε and by definition ρ10 = ε. (These last facts are analogous to (−1)2 = 1 and x0 = 1.)
2c. We have τk = τ1ρ1k for k = 0,1,2,3, as we can check by computing the cycle notation for the left and right sides.
3a. A cube symmetry σ can rotate Face 1 to any of the 6 faces, so there are 6 choices for σ(1). Then σ(2) can be any of the 4 faces adjacent to σ(1). Now σ(3) can only be the face adjacent to σ(1) and σ(2), such that the path σ(1) → σ(2) → σ(3) → σ(1) circles clockwise around their common corner (since the path 1 → 2 → 3 → 1 circles clockwise around their common corner). Finally, σ(4) is the face opposite σ(3), etc. This makes a total of 6 × 4 = 24 choices, so that |G| ≤ 24.
3b. The cube has 1 identity symmetry ε = (1)(2)...(6). Also 3 axes through opposite pairs of faces, each with 1⁄4, 1⁄2, and 3⁄4 rotations, such as: α = (1)(6)(2354) and α2 = (1)(6)(25)(34). Also 4 axes through opposite pairs of corners, each with 1⁄3 and 2⁄3 rotations, such as: (1,2,3)(4,6,5). Also 6 axes through midpoints of opposite pairs of edges, each with a 1⁄2 rotation, such as: (1,2)(3,4)(5,6). Total: 1 + (3)(3) + (4)(2) + (6)(1) = 24, giving all the possible symmetries of G according to part (a).
4a & b. The colorings, grouped into symmetry classes of the rectangle group. Each line lists the elements of c = {c, ρ(c), τ1(c), τ2(c)}, though some of these might be identical, so we only list them once. (Remember, the quarter-turn is not a rectangle symmetry.)
| R | R | |||||||||
| R | R | |||||||||
| B | R | R | R | R | B | R | R | |||
| R | R | R | B | R | R | B | R | |||
| B | B | R | R | |||||||
| R | R | B | B | |||||||
| R | B | B | R | |||||||
| R | B | B | R | |||||||
| B | R | R | B | |||||||
| R | B | B | R | |||||||
| R | B | B | B | B | R | B | B | |||
| B | B | B | R | B | B | R | B | |||
| B | B | |||||||||
| B | B |
We have |C| = 7 symmetry classes (rows) altogether. Thus, we say there are 7 colorings of the rectangle vertices with colors R,B, distinct up to symmetry.
4c. There are |D| = 4! = 24 colorings of 4 vertices with 4 distinct colors, corresponding to lists of 1,2,3,4 in some order. Every symmetry class has |G| = 4 colorings, so the number of symmetry classes is: |D| = |D|⁄|G| = 24⁄4 = 6.
5. |D| = |D|⁄|G| = 6!⁄24 = 30.
HW:
- Using Burnside's Theorem. For each of the following cases, find the number of cycles of each symmetry σ ∈ G Sym(X) ⊂ Sn. (For example, the identity ε = (1)(2)...(n) has cyc(ε) = n cycles.)
We color the n special points of X with k available colors, with no restrictions.
Use Burnside's Theorem
to compute |C|,
the number of symmetry classes of colorings: that is,
kcyc(σ) averaged over all σ ∈ G.
Check your general formula against known answers in the cases k = 1,2.
- X is the rectangle from HW 2/24 #4, coloring n = 4 vertices.
- X is the square from HW 2/24 #2, coloring n = 4 vertices.
- X is the cube from HW 2/24 #3, coloring n = 6 faces.
- Find the number of different necklaces that can be made by stringing 6 red or blue beads on a loop, counting a bead arrangement as the same after it has been moved around (without breaking the necklace). Draw an example of each symmetry type, such as:
which we write compactly by listing the beads in clockwise order from the top: RRBBRB. This is the same as its its rotations BRRBBR, RBRRBB, etc., and its flip RBRRBB by the symmetry τ = (1)(25)(34)(6), etc.R B R R B B
Hints: First determine the natural symmetry group involved. Imagine the beads at the corners of a regular hexagon, with the corners numbered as:
Write each symmetry in cycle notation, and apply Burnside's Theorem. Once you have determined the number of symmetry classes of colorings, use trial-and-error to give that many different colorings: all R's; or 5 R's and 1 B; or 4 R's and 2 B's next to each other, etc.1 6 2 5 3 4 - The figure below, from HHM p.207, shows the rigid carbon skeleton of a molecule (with a nitrogen in the middle):
Here "different" naturally means different up to rotational symmetry in space: two molecules are obviously the same if we can rotate one to the other. These are all the plane symmetries of the skeleton, including flips, which are rotations in 3 dimensions.- Find the group of 6 symmetries of X. For example, τ1 is a flip across the central vertical line in the skeleton, making the permutation τ1 = (1)(2,15)(3,14)(4,13)(5,12)(6,11)(7,10)(8,9). (This flip within the plane can be considered as a 180° rotation in space around the vertical axis.)
Hint: the symmetry group is the same as that of a triangle, but acting on the 15 vertices instead of just 3 corners. - Use Burnside's Formula and its Corollary to determine the number of different hydrocarbon molecules.
- Find the group of 6 symmetries of X. For example, τ1 is a flip across the central vertical line in the skeleton, making the permutation τ1 = (1)(2,15)(3,14)(4,13)(5,12)(6,11)(7,10)(8,9). (This flip within the plane can be considered as a 180° rotation in space around the vertical axis.)
- Let X be a standard 8 × 8 checkerboard, with white and black squares printed on it:

- What are the natural symmetries of X? Remember, a symmetry is a way to move X to itself while preserving its structure (including sizes, shapes, colors, and any other natural features). In other words, the object should look the same before and after you move it. Hint: There are not many symmetries.
- Number the squares on the board 1,...,64 for reference (1,...,8 in in the first row, 9,...,16 in the second row, etc.). Write each symmetry as a permutation of the 64 squares, in cycle notation. Hint: No need to write out all the cycles: write enough to show the pattern, then use "..." notation.
- Now we put on each square a red or blue checker piece, or leave it empty. How many possible arrangements of checker pieces, counting symmetric arrangements as the same?
Examples: 8 red pieces in the top row is equivalent to 8 red pieces in the bottom row, since turning one arrangement gives the other. However, 8 red pieces on the black diagonal (top left to bottom right) is different from 8 red pieces on the white diagonal (top right to bottom left), since it matters whether the checkers are on white or black squares and no turn will make one arrangement look like the other.
Hint: Consider this as a coloring problem, and use Burnside's Theorem.
The case k = 1 clearly has only one coloring, and indeed the formula becomes |C| = 1⁄|G| ∑σ∈G 1cyc(σ) = 4/4 = 1. In the case k = 2, we recover |C| = 1⁄4(24 + 3(22)) = 7 from HW 2/24 #4b.
1b. Referring to HW 2/24 #2a, the identity ε has 4 cycles, the two 1⁄4 rotations have 1 cycle each, the 1⁄2 rotation has 2 cycles, two of the reflections have 2 cycles, and the other two reflections have 3 cycles, Burnside gives the general formula:
|C| = 1⁄8(k4 + 2k3 + 3k2 + 2k).
The case k = 1 gives |C| = 1⁄8 ∑σ∈G 1cyc(σ) = 8/8 = 1, which is correct. In the case k = 2, we get
|C| = 1⁄8(24 + 2(23) + 3(22) + 2(2)) = 6: there is one symmetry class for 0R's, 1R, 3R's, 4R's; and two symmetry class for 2R's 2G's,
namely when the R's are next to each other and when they are diagonal.
1c. Referring to HW 2/24 #3,
the identity gives contribution k6;
the three sets of face rotations like α and α2
give 6k3 + 3k4;
the four sets of corner-rotations give 8k2;
and the six edge-rotations give 6k3.
Thus |C| = 1⁄24(k6 + 3k4 + 12k3 + 8k2).
For k = 1 this gives |C| = 1,
which is correct.
and for k = 2 it is |C| = 10.
There is one symmetry class for 0R's, 1R, 5R's, 6R's; two classes for 2R's (adjacent or opposite) and similarly
for 4R's; and two classes for 3R's (all adjacent or not).
2. We can consider the 6 beads at the corners of a regular hexagon (with vertices labeled 1,...,6 clockwise), so that the symmetry group is D6 (HW 2/24 #2): the identity; 5 rotations ρi = (ρ1)i; three reflections τ1, τ2, τ3 across the lines through opposite pairs of edges; and three reflections τ4, τ5, τ6 across the lines through opposite pairs of vertices:
| σ | cycles | kcyc(σ) |
| ε | (1)(2)(3)(4)(5)(6) | k6 |
| ρ1 | (123456) | k1 |
| ρ2 | (135)(246) | k2 |
| ρ3 | (13)(24)(36) | k3 |
| ρ4 | (531)(642) | k2 |
| ρ5 | (65431) | k1 |
| τ1 | (1)(26)(35)(4) | k4 |
| τ2 | (2)(13)(46)(5) | k4 |
| τ3 | (3)(24)(15)(6) | k4 |
| τ4 | (12)(36)(45) | k3 |
| τ5 | (23)(14)(56) | k3 |
| τ6 | (34)(25)(16) | k3 |
Representatives of the 13 classes:
BBBRRR, BBRRBR, BRBRBR,
BBBBBB, RBBBBB, RRBBBB, RBRBBB, RBBRBB.
| B | R | |
| R B | B R | |
| B R | R B | |
| R | B |
3. The symmetry group is G = D3, the same motions of the plane as for a triangle (see HW 2/27 #2). However, these symmetries are permuting the 15 labeled vertices:
| σ | cycles | kcyc(σ) |
| ε | (1)(2)...(15) | k15 |
| ρ1 | (1,6,11)(2,7,12)(3,8,13)(4,9,14)(5,10,15) | k5 |
| ρ2 | (11,6,1)(12,7,2)(13,8,3)(14,9,4)(15,10,5) | k5 |
| τ1 | (1)(2,15)(3,14)(4,13)(5,12)(6,11)(7,10)(8,9) | k8 |
| τ2 | (6)(5,7)(4,8)(3,9)(2.10)(1,11)(12,15)(13,14) | k8 |
| τ3 | (11)(10,12)(9,13)(8,14)(7,15)(6,1)(5,2)(4,3) | k8 |
4a. The natural symmetries are turning only (since flipping the board would expose the underside). The only turn which does not switch white and black squares is the 180° turn ρ, so the symmetry group is G = Sym(X) = {ε, ρ}.
4b. The identity is ε = (1)(2)...(64). The rotation is ρ = (1,64)(2,63)(3,62)...(32,33) : the 32 two-cycles are all pairs (a,b) with a+b = 65.
4c. There are k = 3 options for each square: red piece, blue piece, or empty. Choosing one of these for each square is a Burnside coloring problem with the above group G = {ε ρ}, so the number of coloring classes (arrangements up to symmetry) is:
HW:
- Apply Polya's Method to the following problems. Use
Wolfram Alpha for expanding when needed: don't injure your brain!
Find representatives of the predicted number of coloring classes.
Symmetry groups include rotations and reflections, as in HW 10/16 #2,3 and HW 10/18 #1.
- X = a rectangle with n = 4 corners colored with k = 2 colors, R,B.
- X = a rectangle with n = 4 corners colored with k = 3 colors, R,B,G. Explain why the generating function "grows" from part (a), adding new terms but not changing the previous terms.
- X = a square with n = 4 corners colored with k = 2 colors R,B. You could think of these as designs for a necklace with 4 beads.
- In chemistry, a benzene ring C6 is a regular hexagon of carbon molecules, each of which can bond to a radical such as H (hydrogen), OH (hydroxyl), or CH3 (methyl). For example:
- Count how many possible drawings with any number of the three types of radicals (for example, all H's, which is plain benzene). In this part, do not consider symmetry, just ways of drawing the molecule. Hint: Very easy.
- Count how many drawings with 2 H's, 2 OH's, and 2 CH3's. Hint: Use basic enumeration techniques.
- Determine the natural symmetry group of the benzene ring in space, and use Burnside's Theorem to count the number of physically different molecules with any number of the three radicals.
Hint: The different drawings of the same molecule correspond to a symmetry class of colorings. Physically different molecules mean different classes of colorings. - Use Polya's Method to count how many physically different molecules with 2 H's, 2 OH's, and 2 CH3's. These are called the chemical's isomers.
1a. Rectangle group G = { ε = (1)(2)(3)(4), τ1 = (12)(34), τ2 = (14)(23), ρ = (13)(24) }.
fε(r,b) = (r + b)4,
fτ1(r,b) = fτ2(r,b) = fρ(r,b) =
(r2+b2)2
Generating function counting symmetry classes of colorings:
For example, the term 3b2r2 means there are 3 symmetry classes of colorings with 2R's, 2B's. These are quite easy to draw.
1b. This time:
= b4 + b3g + 3b2g2 + bg3 + g4 + b3r + 3b2gr + 3bg2r + g3r + 3b2r2 + 3bgr2 + 3g2r2 + br3 + gr3 + r4
It is clear from the first expression that if we set g = 0, we get back the previous generating function from part (a), so the terms in this polynomial are those of the previous one, plus terms involving g.
To find representatives of the predicted coloring classes, we only need to consider cases where all 3 colors appear, since the 2-color cases were all considered in part (a).
1c. Dihedral group D4 = G = { ε = (1)(2)(3)(4), ρ = (1234), ρ2 = (13)(24), ρ3 = (4321), τ1 = (1)(3)(24), τ2 = (2)(4)(13), τ3 = (14)(23), τ4 = (12)(34) }.
= b4 + b3r + 2b2r2 + br3 + r4
Notice that the coefficients are all less than or equal to those in 1(a), since more symmetry gives fewer distinct symmetry classes.
2a. The number of all colorings is: kn = 36 = 729.
2b. The number of colorings of 6 positions distributed into 2+2+2 of the three kinds of radical is the number of ways to pick 2 positions of 6 which are H's; and 2 of the remaining 4 positions which are OH's, and the remaining 2 can only be CH3. Ans: (6 | 2)(4 | 2)(2 | 2) = 90.
2c. The natural symmetry group is the rotations of the molecule in space, which include reflections in the plane: thus we get the dihedral group D6 = G, consisting of 2(6) = 12 symmetries: the identity, 5 rotations, and 6 reflections (see the table below). Burnside's Theorem says the number of symmetry classes with k = 3 colors is:
That is, the 729 drawings from part (a) make only 92 distinct molecules.
2d. Here we sort symmetries by their cycle structure, with the corresponding term in Polya's Theorem. The three chemical radicals (the "colors") are represented by the three generic variables x1, x2, x3:
| σ ∈ G | fσ(x1, x2, x3) | |Cσ| = kcyc(σ) |
|---|---|---|
| ε = (1)(2)(3)(4)(5)(6) | (x1+x2+x3)6 | 36 |
| ρ = (123456), ρ5 = (654321) | (x16+x26+x36) | 31 |
| ρ2 = (135)(246), ρ4 = (351)(624) | (x13+x23+x33)2 | 32 |
| ρ3 = (14)(25)(36), τ4 = (12)(36)(45), τ5 = (23)(14)(56), τ6 = (34)(25)(16) | (x12+x22+x32)3 | 33 |
| τ1 = (1)(4)(26)(35), τ2 = (2)(5)(13)(46), τ3 = (3)(6)(15)(24) | (x1+x2+x3)2 (x12+x22+x32)2 | 34 |
The generating function of the coloring classes C is:
=
x16 + x15x2 + x15x3 + 3x14x22 + 3x14x2x3 + 3x14x32 + 3x13x23
+ 6x13x22x3
+ 6x13x2x32
+ 3x13x33 + 3x12x24
+ 6x12x23x3
+ 11x12x22x32
+ 6x12x2x33 + 3x12x34
+ x1x25
+ 3x1x24x3
+ 6x1x23x32
+ 6x1x22x33
+ 3x1x2x34 + x1x35 + x26 + x25x3
+ 3x24x32
+ 3x23x33 + 3x22x34 + x2x35 + x36
The sum of all the coefficients is just the total number of coloring classes, namely 92 from the previous problem. This is obtained by setting x1 = x2 = x3 = 1, so that Polya's Theorem reduces to Burnside's Theorem.
Extracting the term 11x12x22x32,
we see that there are 11 symmetry classes with 2 H's, 2 OH's, and 2 CH3's.
That is, the 90 drawings from part (b) make only 11 distinct molecules.
- Definitions 1.1.1
- Paths and shells 1.1.2
- Bipartiteness 1.1.3
HW:
- Bob goes to a shop selling 5 kinds of donuts: Plain, Glazed, Chocolate, Strawberry, Boston (P,G,C,S,B).
Count how many ways to choose donuts, under the following conditions:
- A bag of 3 donuts, all different. Ex: Plain, Chocolate, Strawberry.
- A bag of 3, but they need not be different. Ex: 1 Plain, 2 Chocolates.
- A bag with any number of donuts (but at least 1), all different. Ex: The most he could get is 1 of every kind.
- Every lunchtime Mon-Fri, a bag of 3 donuts, all different in each bag.
Ex: Mon P,G,S; Tue G,C,B; Wed G,C,B; Thu P,C,S; Fri C,S,B.
- In the same store, the 5 kinds of donuts are displayed in bins next to each other.
Count how many arrangements under the following conditions:
- 5 bins: 1 of each kind, no restrictions. Ex: from left-to-right, B,C,G,S,P.
- Same as (a), but the Chocolate cannot be next to the Boston. Ex: B,G,C,S,P
- Same as (a), but the Chocolate cannot be next to the Boston or the Strawberry. Ex: B,G,C,P,S.
- 6 bins: 2 identical bins of Chocolate, 1 each of the other 4 kinds. Ex: G,B,C,P,C,S.
- You Can't Have Just One: Suppose you choose 20 jellybeans of 3 kinds (red, green, yellow), with the rule that you cannot choose just one of any kind. That is, if you choose any reds, you must take at least 2 of them, and the same way with greens and yellows.
Let a be the number of ways to choose such a handful.
- Use positive counting (Sum and Product Principles) to find a.
- Use negative counting (PIE) to find a.
- Use the Method of Generating Functions to find a.
- Step 0: Generalize a to a sequence ak.
- Step 1: Use the combinatorics of choosing to find a simple formula for the generating series f(x) = ∑k≥0 akxk.
- Step 2: Use algebra and known series to expand f(x) as a Taylor series. Equating the coefficients of this final series with the original ak solves our problem.
- Consider the following recurrence:
pk = 3pk−1 − 2pk−2
for k ≥ 2,
with p0, p1 being arbitrary given constants.
Ex: In the special case p0 = p1 = 1, we get p2 = 3(1)−2(1) = 1, p3 = 3(1)−2(1) = 1, etc.
Solve by the Method of Generating Functions, giving an explicit, non-recursive formula for pk. - Board games.
- In the One-Step Game, for each turn you either stay in place, or advance one step.
How many possible outcomes in 8 turns?
Example: The 8 turns are: step, stay, stay, step, stay, step, step, stay. - In the One-Step Game, how many ways can you advance 5 steps in 8 turns?
Example: step, stay, stay, step, stay, step, step, step. - In the Many-Step Game, for each turn you advance any number of steps: 0,1,2,3,....
How many ways can you advance 5 steps in 8 turns?
Example: 1 step, 0 steps, 0 steps, 3 steps, 1 step, 0 steps, 0 steps, 0 steps.
- In the One-Step Game, for each turn you either stay in place, or advance one step.
How many possible outcomes in 8 turns?
- For each game below, use the Generating Function Method to compute the sequence:
ak = number of ways to advance k steps in 8 turns. Hint: Consider possible outcomes in turn 1,..., turn 8, and translate this into algebra.- Compute ak for 8 turns of the One-Step Game from 6(a).
- Compute ak for 8 turns of the Many-Step Game from 6(c).
- Compute ak for 8 turns of the Odd-Step Game, where for each turn, you advance an odd number of steps: 1,3,5,....
Explain your formula for ak by solving the problem with positive-counting methods. The formula itself and the computations of Step 2 hint at a useful transformation. - Compute ak for 8 turns of the Ten-Step Game where each turn can be any number of steps from 0 to 10. Hint: This is similar to the dice problem in HW 2/8 #5, but Step 2 is more complicated. You can also do Step 2 by brute force, with Wolfram Alpha.
- Pascal's Triangle and Deletion Transform
- State the recurrence formula for choose-numbers (n | k) which we use to construct Pascal's Triangle. Recall the transformation proof of this recurrence: we transform the objects counted on the left side (sets S with k distinct elements from n) into objects counted by the right side (sets S' with k or k−1 elements from {1,...,n}).
- The equivalent of Pascal's Triangle for multi-choose numbers is given by the recurrence:
((n | k)) = ((n−1 | k)) + ((n | k−1)). We can prove this by transformation from the objects counted by the left side (multi-sets M with k objects of n kinds), into objects counted by the right side (multi-sets M' with k elements of n−1 kinds, or with k−1 elements of n kinds). The transformation is defined as follows on a multiset M.- If M does not contain n, let M' = M
- If M has at least one copy of n, let M' = M − {n}, the same except with one fewer copy of n.
- Define the inverse of the transformation in (b). Given M', how to produce M?
- One of the objects counted by the Catalan number Ck is
the ways to parenthesize an expression with k multiplications.
Example for C4: (x0(x1x2))(x3x4).
Problem: Make a two-column table of the transformation between C4 and C0C3 + C1C2 + C2C1 + C3C0 . You must use a clear rule to split each expression into left and right parts.
Note: It is not completely unreasonable to consider items in a bag as ordered, which would lead to Basic Problem 2, ans: 53. It is wise to state in your answer which interpretation you use.
1b. Here a bag is a multi-set with 3 items of 5 kinds (Basic Problem 4). Ans: ((5 | 3)) = (5+3−1 | 3) = (7 | 3) = 73 / 3! = 35.
1c. A bag is any non-empty subset of {P,G,C,S,B}. An n-element set has 2n subsets (since each of the n elements could be in or out of the subset: Product Principle). Since the empty set is not allowed, we get 25 − 1 = 31.
1d. A sequence of 5 independent choices, each with (5 | 3) possibilities (Product Principle). Ans: (5 | 3)5 = 100,000.
2a. Basic Problem 1: Ordering 5 distinct objects (Basic Problem 1). Ans: 5! = 120.
2b. PIE: A = {all arrangements from part (a)}, A1 = {arrangements containing sequence C,B}, A2 = {arrangements containing sequence B,C}. In A1, we can consider the adjacent letters C,B as a single unit, next to the 3 other units P, G, S; and these 4 units can be arranged arbitrarily. Same for A2, so |A1| = |A2| = 4!. Also |A1∩A2| = 0, and the number of good arrangements is:
2c. PIE: A = {all arrangements}, with 4 kinds of forbidden arrangements: A1 = {arrangements containing the sequence C,B}, A2 = {arr with B,C}, A3 = {arr with C,S}, A4 = {arr with S,C}. Reasoning as before, |A| = 5! and |Ai| = 4!. The only non-empty intersections are: A1∩A4 = {arr with S,C,B} and A2∩A3 = {arr with B,C,S}. Again, consider arbitrary arrangements of a 3-letter unit with two 1-letter units, giving 3! arrangements for each intersection. Hence:
− ∑1≤i<j<k≤4 |Ai∩Aj∩Ak| + |A1∩A2∩A3∩A4|
= 5! − 4(4!) + 2(3!) = 36.
Another way: positive counting using a transformation. We analyze the data into parts which can be easily counted.
- From a good arrangement like (C,G,S,B,P), we cross out the two letters S,B to extract (C,G,P); and we extract the other two letters (S,B). Now, in the original arrangement, replace C,G,P by bin dividers,and S,B by beans: ( | | O O | ), meaning the first two bins are empty, the third bin contains two beans, the fourth bin is empty. Now, S,B cannot be next to C, so we erase these two empty bins and their adjacent dividers to get: ( O O | ).
- No information has been lost, since these three pieces of data (C,G,P), (S,B), ( O O | ) are enough to reconstruct the original good arrangement. From seeing C at the beginning of (C,G,P), we know the two erased bins must be at the beginning, giving ( | | O O | ); and now we can replace the three dividers and two beans by the corresponding letters to recover (C,G,S,B,P).
- We can reverse-transform any data of the same type, such as: (P,C,G), (B,S), ( O | O ). From (P,C,G), we know that the two erased bins were in the center (next to C), so the bin arrangement was: ( O | | | O ) and we re-construct the original arrangment by replacing the dividers and beans with the corresponding letters: (B,P,C,G,S).
- Therefore the number of good arrangements is equal to the number of data triples above: ways to arrange {P,G,C}, which is 3!, times the ways to arrange {B,S}, which is 2!, times the ways to put O O into two bins ( | ), which is ((2 | 2)). Final answer: 3! 2! ((2 | 2)) = 6 (2) (3) = 36.
2d. Pick the positions of the two C's (Basic Problem 3), then arrange the other 4 around them (Basic Problem 1). Ans: (6 | 2) 4! = 360.
Alternatively: list the positions of B,G,S,P, making a list of 4 distinct positions out of 6 (Basic Problem 2). Ans: 64 = 360.
3a. Positive counting. Split all outcomes into disjoint cases (Sum Principle): Case (i), just 1 flavor, all 20 beans the same: 3 handfuls. Case (ii), have 2 flavors: then 4 beans are fixed (2 of each flavor), with 16 left to choose among 2 flavors; (3 | 2)((2 | 16)) handfuls. Case (iii), have all 3 flavors: then 6 beans are fixed, 14 left to choose among 3 flavors; ((3 | 14)) handfuls. Ans: 3 + 3((2 | 16)) + ((3 | 14)) = 3 + 3(17 | 1) + (16 | 2) = 174
3b. Negative counting (PIE). A = {all handfuls of 20 beans of 3 kinds}, Ai = {just 1 of flavor i, the other 19 of 2 flavors}, for i = 1,2,3. Ans: ((3 | 20)) − (3 | 1)((2 | 19)) + (3 | 2)((1 | 18)) − (3 | 3)((0 | 17)) = (22 | 2) − 3(20 | 1) + 3 = 174.
3c. Step 0: Generalize the problem to give a sequence.
Let ak be the number of ways to choose k jellybeans with the given restriction.
Step 1. Find a simple formula for the generating function f(x) = ∑k≥0 ak xk .
Consider that a handful of beans can be chosen by the logical expression:
Using the first expression:
= ∑k≥0 ((3 | k))xk − ∑k≥0 3((2 | k))xk+1 + ∑k≥0 3xk+2 − x3
Alternatively, using the second expression:
= 1 + ∑k≥0 3xk+2 + ∑k≥0 3((2 | k))xk+4 + ∑k≥0 ((3 | k))xk+6
4. Turning the recurrence into an equation for f(x) = ∑k≥0 pkxk, we get:
= p0 + p1x + 3x∑k≥2 pk−1x k−1 − 2x2∑k≥2 pk−2xk−2
= p0 + p1x + 3x (f(x) − p0) − 2x2f(x)
| f(x) | = |
| . |
5a. A sequence of 8 independent choices, with 2 outcomes for each. Product Principle: 28 = 256.
5b. A sequence of 8 binary choices, with 5 steps and 3 stays. Position Transformation into Basic Problem 3: (8 | 5) = (8 | 3) = 56.
5c. A sequence of 8 whole numbers adding up to 5, (n1,..., n8) with ni ≥ 0 and n1 + ... + n8 = 5. The Multiplicity Transformation turns this into arrangements of 5 beans in 8 bins, Basic Problem 4: ((8 | 5)) = (5+8−1 | 5) = (12 | 5) = 792.
6a. Step 1: (Take 8 turns stay/step) ⇔
(turn 1: stay or step) and ... and (turn 8: stay or step).
Since "stay" advances 0 steps, it is replaced by x0, and similarly "step" becomes x1:
Step 2: Binomial Series: f(x) = Σk=08 (8 | k)xk, so ak = (8 | k), as in 6(b).
6b. Step 1: (Take 8 turns of any length) ⇔
(turn 1: 0 steps or 1 step or 2 steps or...) and ... and (turn 8: 0 steps or 1 step or ...).
Each choice to advance i steps gets replaced by xi:
Step 2: Negative Binomial Series: f(x) = Σk≥0 ((8 | k))xk, so ak = ((8 | k)), as in 6(c).
6c. Step1: Similarly to the above:
We can see that the coefficient of of an even power xk is: ak = ((8 | ½(k−8) )). Also, the coefficient of an odd power xk vanishes: ak = 0.
Retrospective: To solve this problem by elementary methods, consider any way to advance k steps in 8 odd-step turns.
- There is at least one step per turn, so fix that one step and forget about it (8 times).
- The remaining part of each turn advances an even number of steps, for a total of k−8 steps in 8 turns.
- This is the same as advancing any number of double-steps per turn, for a total of k' = ½(k−8) double-steps in 8 turns.
- This reduces the problem to the previous case 7(b), so the answer is ((8 | k')) = ((8 | ½(k−8) )).
6d. f(x) = (1+x+x2+...+x10)8
=
(1−x11)8⁄(1−x)8
=
(∑8i=0
(−1)i (8 | i) x11i)
(∑j≥0 ((8 | j)) xj),
so ak = ∑11i+j=k (−1)i (8 | i) ((8 | j))
7a. The recurrence is: (n | k) = (n−1 | k) + (n−1 | k−1). The Deletion Transformation is S → S' where: S' = S if n ∉ S; and S' = S \ {n} if n ∈ S. Its inverse is the Insertion Transformation S' → S, where S = S' if |S'| = k, and S = S' ∪ {n} if |S'| = k−1.
7b. Each input M is on top, with its transformation output M' below it.
| M = | {1,1,1} | {1,1,2} | {1,1,3} | {1,2,2} | {1,2,3} | {1,3,3} | {2,2,2} | {2,2,3} | {2,3,3} | {3,3,3} |
| M' = | {1,1,1} | {1,1,2} | {1,2,2} | {2,2,2} | ||||||
| {1,1} | {1,2} | {1,3} | {2,2} | {2,3} | {3,3} |
The inputs cover all ((3 | 3)) multisets M; the outputs cover all ((2 | 3)) + ((3 | 2)) multisets M'.
7c. The inverse is the Insertion Transformation M' → M, where: M = M', if |M'| = k; and
8. We make a two-row table of the transformation between the 14 factorizations counted by C4, and the splitting of these at the outermost multiplication into pairs of factorizations counted by ∑3i=0 CiC3−i. In fact, the most practical way to list all the C4 expressions at all is to write the (Ci | C3−i) expressions first, then combine them.
| C4 | x0(x1(x2(x3x4))) | x0(x1((x2x3)x4)) | x0((x1x2)(x3x4)) | x0((x1(x2x3))x4) | x0(((x1x2)x3)x4) |
| C0 | C3 | x0 | x1(x2(x3x4)) | x0 | x1((x2x3)x4) | x0 | (x1x2)(x3x4) | x0 | (x1(x2x3))x4 | x0 | ((x1x2)x3)x4 |
| C4 | (x0x1)(x2(x3x4)) | (x0x1)((x2x3)x4) | C4 | (x0(x1x2))(x3x4) | ((x0x1)x2))(x3x4) |
| C1 | C2 | x0x1 | x2(x3x4) | x0x1 | (x2x3)x4 | C2 | C1 | x0(x1x2) | x3x4 | (x0x1)x2) | x3x4 |
| C4 | (x0(x1(x2x3)))x4 | (x0((x1x2)x3))x4 | ((x0x1)(x2x3))x4 | (((x0(x1x2))x3)x4 | (((x0x1)x2)x3)x4 |
| C3 | C0 | x0(x1(x2x3)) | x4 | x0((x1x2)x3) | x4 | (x0x1)(x2x3) | x4 | ((x0(x1x2))x3 | x4 | ((x0x1)x2)x3 | x4 |
We defined a (simple) graph G = (V,E) by giving its set of vertices V = {v1, v2,.., vn} and its edges E = {e1, e2,.., em}. Each edge is an unordered pair of vertices, officially a set e = {vi , vj}, but for convenience we write e = vivj = vjvi .
HW:
- Ch 1.1.1, p. 4, Ex 1, 2, 3. Model each relationship by a graph, a digraph (directed graph with one-way edges) or a multi-graph (graph with multiple edges and/or loop edges).
- The complete graph G = Kn (see p. 10) is the graph with n vertices V = {v1, v2,.., vn}, and all possible edges between these vertices: E = {vivj for i < j}. For example, K3 has V = {v1, v2, v3} and
E = {v1v2, v1v3, v2v3}
- Draw Kn for n as high as you can. For example, K3 is a triangle graph with |E| = 3, K4 can be drawn as a square with the two diagonals, etc.
- Determine the number of edges |E|, which depends on n.
- Cube graphs. The graph Cub3 is defined as follows: the vertices are the corners of a unit cube in 3-dimensional space: (0,0,0), (1,0,0),...,(1,1,1). The edges correspond to edges of the solid cube, and go between vertices which differ in only one coordinate, such as (1,0,1) and (1,1,1). For brevity, we can write the vertices as bit-strings 000, 100, 010,..., 111.
- Draw the cube graph. You could draw a sketch of a cube and label the vertices. Alternatively, write the vertices in levels depending on the number of 1's: 111 at the top, then below it 110,101, 011, and so on; then draw the appropriate edges.
- The hypercube graph Cub4 has the same combinatorial construction, but in 4 dimensions. You can't picture this (unless you have a very good geometric intuition), but you can easily define the vertices and edges.
The vertices are bit-strings 0000, 1000, 0010,..., 1111, and an edge goes between any two vertices that differ in only one coordinate, such as 1010 and 1110.
Problem: How many vertices and edges in Cub4? - Draw Cub4. You can't easily sketch the 4-dimensional cube, but you can use the top-to-bottom method: 1111 at the top, then below it 1110, 1101, 1011, 0111, and so on; then drawing the appropriate edges. Warning: not every pair of vertices in adjacent levels are connected by an edge, only those that differ in only one coordinate.
- Extra Credit: Try to draw the graph Cub4 in a way that helps to visualize the 4-dimensional cube. Perhaps use the analogy with Cub1 = line segment, Cub2 = square = two line segments with corresponding vertices connected, and Cub3 = two squares with corresponding vertices connected.
- Extra Credit: Find the number of vertices and edges for the d-dimensional hypercube Cubd . Use coordinates (x1,x2,x3,x4) to describe the points of a 2-dimensional and 3-dimensional faces of Cub4, or more generally n-dimensional faces of Cubd, and find how many of each.
- Let G be a graph with n vertices, with deg(v) = d, a constant for all v ∈ V. We say G is regular of degree d, or d-regular.
- Describe all possible 1-regular graphs.
- Draw all possible graphs with 5 vertices (draw them without labels) in which 4 of the vertices have degree 3. In particular, show that the last vertex must have degree 0, 2 or 4, but 1 and 3 are impossible. Thus, there is no 3-regular graph with 5 vertices.
- Give a short proof that for any regular graph G, either d or n must be an even number. Hint: Use the Vertex-Edge Formula (Graph Notes I.8).
- Extra Credit: Show the converse of the previous part. That is, for any pair (d,n) with d < n and d or n even, give an example of a d-regular graph with n vertices.
Hint: Start with Cn .
- Extra Credit: Write a computer program implementing the walk-to-path algorithm from class. The input is a walk along edges of some graph: a list of vertices with possible repeats. The output should be a path along edges of the graph: a list of vertices (which you can represent as numbers or characters) with all loops and repeats cut out. Try to optimize the algorithm to make it more efficient.
1. (p. 4 #1) V = {a,b,c,d,e,f,g,h,i,j} and E = {all possible edges xy}−{af, bg, ch, di, ej}. That is, G is the complement of the graph with edges {af, bg, ch, di, ej}.
1. (p. 4 #2) V = {A,B,C,D,E,F}, E = {AD, BA, BE, CD, CE, DC, FA, FB}. This should be a digraph, so that AD ≠ DA, since Adam likes Doug is not the same as Doug likes Adam. Officially, each directed edge is an ordered pair like (A,D). Note that it is reasonable to ignore the loop-edge EE, since it does not denote a valid roommate pairing.
1. (p. 4 #3) V = {teams}, with an edge between each pair of teams that have played each other, and two edges between teams that have played twice. This is is a multi-graph since it has multiple edges between a given pair of vertices.
2b. |E| = (n | 2) = ½n(n−1)
3a.
3b. n = |V| = 24 = 16. Since Cub4 is 4-regular, the Vertex-Edge Formula gives |E| = ½nd = ½(16)(4) = 32.
4a. A 1-regular graph is a union of disjoint edges: V = {a_1,...,a_n, b_1,..., b_n} and E = {a_1b_1, a_2b_2,..., a_nb_n}.
4b. Set d = deg(5), the number of edges from vertex 5. For d = 0, G = K4 ∪ K1 ; for d = 2 , G has edges E = {51, 52, 31, 32, 34, 41, 42}; and for d = 4 , G has E = {51, 52, 53, 54, 12, 23, 34, 41}. For d = 1 , vertex 5 must connect to some vertex, say 1; and then 2 must connect to 1,3,4; and 3 must connect to 1,2,4; and 4 must connect to 1,2,3. But this gives deg(1) = 4, so d = 1 is impossible. For d = 3 , vertex 5 must connect to three vertices, say 1,2,3. Then 4 must connect to 1,2,3. Now there are three dangling edges 1?, 2? and 3?, and it is impossible to join them up, so d = 3 is impossible.
4c. Use that ∑v∈V deg(v) = 2|E|, so if deg(v) = d for all n vertices, we have dn = 2|E|. If d and n were both odd, then their product dn would also be odd, but dn = 2|E| is clearly even. This contradiction shows d and n cannot both be odd.
HW:
- Let G = K5, the complete graph with vertices V = {1,2,3,4,5} and all possible edges.
For each type of structure, count how many are possible inside G.
- Paths, meaning lists of successive neighboring vertices, with no repeats. Hint: Consider paths with 0 edges, 1 edge,..., 4 edges, and remember that the reverse of a path is the same subgraph, and hence is considered to be the same path.
- Walks with k steps, meaning lists of k successive neighboring vertices with repeats allowed. (Here k is a fixed positive number.) Also, a walk is not defined by a subgraph, so we count the reverse walk as different.
- Cycles of length k in G. Each cycle is a set of k vertices and k edges in G which form a copy of the cycle-graph Ck, having vertices v1,..., vk and edges v1v2 , ... , vk−1vk and vkv1. (Note that the cycle does not have a "first point" or a direction.)
- Consider the grid graph G below:
e = (i,j)(i+1,j), or e = (i,j)(i,j+1), or e = (i,j)(i+1,j+1). Starting with the vertex v = (3,2) circled in the picture, define the shells D0, D1, D2, .... by starting with D0 = {(3,2)}, and using the recursive construction of Di+1 as the set of neighbors of Di which were not already visited:Di+1 = N(Di) \ (D0 ∪ ... ∪ Di−1). For example, D1 = {(2,1), (3,1), (2,2), (4,2), (3,3), (4,3)}, all the neighbors of (3,2). In fact, Di is the set of vertices which are i edge-steps away from (3,2).- Compute all the shells Di by labeling (3,2) with 0, its neighbors with 1, their neighbors with 2, etc. Furthermore, as you label each vertex with a number i, draw an arrow pointing to its neighboring vertex labeled i−1.
- Use the above labels and arrows to find the distance between (3,2) and (0,5), and to find a shortest path between them. Is this path unique, or is there another shortest path?
- Find the longest possible path from (3,2) to (0,5).
- Consider the modified grid graphs G with the same vertices as above,
V = {(i,j) with 0 ≤ i, j ≤ 5},
but with edges given by either (a) or (b) below.
Questions: Is G connected? That is, is there a path along edges of G between any two vertices? If not, determine the connected components (the maximal sets of vertices which are connected to each other), either as explicit sets or by a representative vertex for each component.- E contains all edges of the form e = (i,j)(i+2,j) or e = (i,j)(i,j+2) or e = (i,j)(i+1,j+1).
- E contains all edges of the form e = (i,j)(i+2,j) or e = (i,j)(i,j+2) or e = (i,j)(i+2,j+2).
1b. A walk is a path with repeat vertices allowed, but without the same vertex twice consecutively. Thus, the number of walks with j vertices is 5(4j−1). If we take k steps along j = k+1 vertices, this becomes 5(4k).
1c. A cycle of length k in K5 is a list of any k vertices, up to the 2k dihedral symmetries of a regular k-gon. Answer: 5k⁄2k .
2a. You should find the shells by labeling the vertices of the graph as described in the problem, and the vertices labeled with each value i form the set Di. To check your answer:
D2 = {(1,0), (2,0), (3,0), (1,1), (4,1), (1,2), (5,2), (2,3), (5,3), (3,4), (4,4), (5,4)},
D3 = {(0,0), (4,0), (0,1), (5,1), (0,2), (1,3), (2,4), (3,5), (4,5), (5,5)},
D4 = {(0,3), (1,4), (2,5),(5,0)}, D5 = {(0,4), (1,5)}, D6 = {(0,5)}.
2b. Since (0,5) ∈ D6, this vertex is 6 steps from (3,2). Stepping from (0,5) to a neighboring vertex with a smaller label, and repeating, we get many possible paths to (3,2) with 6 steps (7 vertices), such as:
2c. It is not hard to find a path containing 35 of the 36 vertices: for example, go around the outer square and spiral inward. I do not know if there is a path using all 36 vertices, which is called a Hamiltonian path. In general, finding a Hamiltonian path is a difficult (NP complete) problem, with no efficient algorithms. Extra Credit if you find one!
3a. If (a,b) is a vertex with a+b an even number, then every edge (a,b)(a+1,b) or (a,b)(a,b+2) or (a,b)(a+1,b+1) will connect (a,b) to a vertex (c,d) with c+d also even; and similarly if a+b odd. Furthermore, if a+b and c+d are both even, it is not difficult to connect them by edges; and similarly for both odd. Hence the connected components are the subgraphs with vertices V1 = {(a,b) with a+b even} and V2 = {(a,b) with a+b odd}.
3b. There are 4 components, each with a typical representative vertex (a,b):(1,1) ∈ V2 = {(a,b) s.t. a,b odd} (1,0) ∈ V4 = {(a,b) s.t. a odd, b even}
Proof by mathematical induction: HHM p. 139-140, Khan Academy video.
HW:
- The following families of graphs are defined in Sec 1.1.3. For each family, answer the following:
for which values of n is this a bipartite graph? If yes, give a partition of its vertices into V = V+ ∪ V− such
that all edges run between these parts, never within V+ or within V−. For graphs which are not bipartite, identify an odd cycle.
- Complete graph Kn , n≥1 .
- Cycle Cn , n≥3 .
- Path Pn , where n≥1 .
- Cube and hypercube graphs Cub3, Cub4 from HW 3/14 #3. Also the d-dimensional hypercube graph Cubd for any dimension d.
- G is the 10-vertex Petersen graph on HHM p. 65:
- The cycle C4 is bipartite, with vertices V = {1,2,3,4} arranged clockwise, partitioned V = {1,3} ∪ {2,4}.
- The complete graph K4 contains the odd cycle C3 with edges 12, 23, 31.
- Counting edges of bipartite graphs.
- The complete bipartite graph Kr,s (where r,s ≥ 1) has two kinds of vertices: V+ = {a1,..., ar} and V− = {b1,..., bs}; and all possible edges between the two kinds: E = {aibj for all i,j}.
Question: How many edges in Kr,s? - Let G be a bipartite graph with 7 vertices. What is the maximum possible number of edges for G? (For example, G cannot be a complete graph K7, since this is not bipartite, so |E| < (7 | 2) = 21.)
- The complete bipartite graph Kr,s (where r,s ≥ 1) has two kinds of vertices: V+ = {a1,..., ar} and V− = {b1,..., bs}; and all possible edges between the two kinds: E = {aibj for all i,j}.
- Recall the cube graph G = Cub3 from HW 3-14 #3.
- Show that G is bipartite by spliting its vertices as V = V+ ∪ V− and checking that all edges go between the two parts, none within one part.
- The cube graph G does not contain the edge e = (000)(110), a diagonal between opposite corners of a square. Let G' = G+e mean the graph with the same vertices as G, and one extra edge. (Thus, if G =(V, E), then G' = (V, E') with E' = E∪{e}.)
Question: Is G' bipartite? - True or false: If e is any edge not already in the cube graph G, then G' = G+e is never bipartite.
- Mathematical Induction
- Goal: Prove a propostion P which involves a whole number n = 1, 2, 3,... Let P(n) denote the case of the proposition for a particular value of n.
- Base Case: Directly check that P(1) is true. (Sometimes we take the base case n = 0 or some other n = n0, to prove P(n) for all n ≥ n0.)
- Chain Case
- Chain-case hypothesis (inductive hypothesis): For some k ≥ 1, assume P(k) is true. (In fact, we may assume all the cases P(1), P(2),..., P(k).) That is, the statement has been checked up to some value n = k.
- Chain-case conclusion: Use your certainty about the case n = k to deduce the next case n = k+1. That is, prove the implication P(k) ⇒ P(k+1) for any k ≥ 1.
- Final conculsion: P(n) is true for all n ≥ 1, i.e. for all n after the base case. This is because we have proved P(1), and the chain of implications P(1) ⇒ P(2) ⇒ P(3) ⇒ ....
- 1 + 2 + 3 + ... + n = ½ n(n+1)
- 1 + 3 + 5 + ... + (2n−1) = n2
- n + 1 ≤ 2n
1b. Cycle Cn with vertices numbered clockwise V = {1,2,...,n} is bipartite if n even, with partition V = {1,3,...,n−1} ∪ {2,4,...,n}; and non-bipartite if n odd (in which case the whole graph is an odd cycle).
1c. Path Pn with vertices numbered in order V = {1,2,...,n} is always bipartite, with the following partition: if n even, V = {1,3,...,n−1} ∪ {2,4,...,n}; if n odd, V = {1,3,...,n} ∪ {2,4,...,n−1}.
1d. Cubd, with vertices v which are bit-strings of length d, is always bipartite, with V+ being the set of bit-strings with an even number of 1's, and V− the bit-strings with an odd number of 1's.
1e. Every cycle of the Petersen graph is a C5, so it is not bipartite.
2a. We have deg(ai) = s edges at each vertex a1,...., ar, and these are the only edges, so |E| = rs. Alternatively, using the Edge-Vertex Formula, |E| = ½(∑i=1r deg(ai) + ∑j=1s deg(bj)) = ½(rs + sr) = rs.
2b. Since G is bipartite, it has a splitting V = V+ ∪ V− with |V+| = r and |V−| = s for some r+s = 7. Given such a splitting, we can add all possible edges between the two parts until we get a complete bipartite graph Kr,s. Thus, the maximum number of edges is rs for some r+s = 7, namely (1)(6) = 6 or (2)(5) = 10 or (3)(4) = 12, and largest of these is 12.
3a. Let V+ = {(000), (110), (101), (011)} and V− = {(100), (010), (001), (111)}, the vertices whose coordinates have an even/odd number of 1's. Since any edge changes exactly one coordinate, it will always change an even number of 1's to an odd number, and vice versa. Thus, all edges go between the + and − vertices, never connecting two + vertices or two − vertices.
3b. The graph G' has the 3-cycle: C = (000)(100)(110)(000). A bipartite splitting of the vertices of G would also give one for C, which is impossible, so there cannot be any splitting for G.
3c. False. G is not a complete bipartite graph, meaning it does not have every possible edge between V+ and V−. In fact, we can add the long diagonals (000)(111) and (001)(110) and (010)(101) and (100)(011) to make the complete bipartite graph K4,4.
4a. Proposition P(n): 1 + 2 + 3 + ... + n = ½ n(n+1)
Proof. Base Case: The left side of equation P(1) is 1, and the right side is ½ 1(1+1) = 1. Thus equation P(1) is true.
Chain Case: Assume we know the formula for n = k, namely P(k): 1 + 2 + ... + k = ½ k(k+1).
We wish to prove it for n = k+1, so we compute the left side of P(k+1):
| 1 + 2 + 3 + ... + k + (k+1) | = | ½ k(k+1) + (k+1) | by the inductive hypothesis P(k) |
| = | (k+1) (½k+1) = ½ (k+1) (k+2) | by algebra (factoring out k+1) |
Conclusion: P(n) is true for all n = 1,2,3,....
4b. Proposition P(n): 1 + 3 + 5 + ... + (2n−1) = n2
Proof. Base Case: The left side of P(1) is 1, and the right side is 12 = 1, so P(1) is true.
Chain case: Assume we know the formula for n = k, namely P(k): 1 + 3 + ... + (2k−1) = k2.
We wish to prove it for n = k+1, so we compute the left side of P(k+1):
| 1 + 3 + 5 + ... + (2k−1) + (2k+1) | = | k2 + (2k+1) | by the inductive hypothesis P(k) |
| = | (k+1)2 | by algebra. |
Conclusion: P(n) is true for all n = 1,2,3,....
4c. We write this one less formally. I claim that k+1 ≤ 2k for all k ≥ 1. The base case k = 1 is true: 1+1 ≤ 21. For the chain case, assume k + 1 ≤ 2k. Then the next case is:
HW: Start on the Hand-in Proofs due 3/28 below.
In #2−5, prove each proposition using the definitions and results in the Graph Notes.
- Practice with logic. If P and Q are statements, we can form the implication statement P ⇒ Q, i.e. "If P, then Q" or "P guarantees Q". A statement equivalent to P ⇒ Q is the contrapositive Not(Q) ⇒ Not(P). A statement quite different and independent from P ⇒ Q is the converse Q ⇒ P.
For each pair of statements below, write out:
- the original implication P ⇒ Q
- the contrapositive: Not(Q) ⇒ Not(P)
- the converse: Q ⇒ P
- the contrapositive of the converse (i.e. the inverse): Not(P) ⇒ Not(Q).
- P: It is raining. Q: I carry an umbrella.
- P: Joe is hungry. Q: Joe eats a whole pie.
- P: The whole number n is the square of an even number. Q: n is divisible by 4.
- P: G is a bipartite graph. Q: Every subgraph of G is bipartite.
- Proposition: Any tree is a bipartite graph.
- The converse of the proposition in #2. Prove this, or disprove by giving a counter-example.
- Proposition: If a tree T has a vertex of degree d, then T has at least d leaves.
Hint: Use the same strategy to find d leaves as I used in the proof for 2 leaves. - A forest is a disjoint union of trees with no edges between them, or equivalently a graph whose connected components are all trees.
- Prove that an acyclic graph is a forest.
- Find the number of edges in a forest with k tree components.
- Extra Credit: Let T be a tree with n vertices, |T| = n. We say a vertex c is a central vertex if removing c splits T into smaller trees T − c = T1 ∪ T2 ∪ ..., each having fewer than half the vertices of T: i.e., |Vi| < ½ n, where Ti = (Vi, Ei). We say an edge e = bc is a central edge if removing e (but not the endpoints b,c) splits T into two trees T − e = T1 ∪ T2 , each having half the vertices of T: i.e., |Vi| = ½n. Prove the following:
Proposition: Every tree has either a unique central vertex or a unique central edge.
Note: This concept of center is due to Otter, and is different from the "distance center" in HHM Sec 1.3.2, p. 36, Thm 1.15, which is obtained by removing successive layers of leaves. For example, the tree with 7 vertices and edges E = {14, 24, 34, 45, 56, 67} has Otter center c = 4 (since the remaining trees are of size 1,1,1,3 < 7⁄2), but the distance-center is 5 (since a maximal path from 5 has length 2, which is shorter than the maximal path from any other vertex).
Not(Q) ⇒ Not(P): If I am not carrying an umbrella, then it is not raining. (Plausible: equivalent to the previous)
Q ⇒ P: If I carry an umbrella, then it is raining. (Not very plausible: I might carry it as a precaution.)
Not(P) ⇒ Not(Q): If it is not raining, then I don't carry an umbrella. (Equivalent to the previous)
1b. P ⇒ Q: If Joe is hungry, then he eats a whole pie. (Not plausible: he will probably eat only a piece.)
Not(Q) ⇒ Not(P): If Joe doesn't eat a whole pie, then he must not be hungry. (Equivalent to previous.)
Q ⇒ P: If Joe eats a whole pie, then he must be hungry. (Plausible!!)
Not(P) ⇒ Not(Q): If Joe is not hungry, then he won't eat a whole pie. (Equivalent to the previous.)
1c. P ⇒ Q: If n = (2m)2 for some m, then n is divisible by 4. (True, since (2m)2 = 4m2.)
Not(Q) ⇒ Not(P): If n is not divisible by 4, then n ≠ (2m)2 for any m. (True: equivalent to the previous.)
Q ⇒ P: If n is divisible by 4, then n = (2m)2 for some m. (False, since n = 8 is divisible by 4, but 8 is not a square number.)
Not(P) ⇒ Not(Q): If n ≠ (2m)2 for any m, then n is not divisible by 4. (False: equivalent to the previous.)
1d. P ⇒ Q: If G is bipartite, then every subgraph is bipartite. (True, since a bipartite splitting of the vertices of G restricts to a splitting of any subgraph.)
Not(Q) ⇒ Not(P): If some subgraph of G is not bipartite, then G is not bipartite. (True: equivalent to the previous.)
Q ⇒ P: If every subgraph of G is bipartite, then G is bipartite. (True, since G itself is a subgraph of G.)
Not(P) ⇒ Not(Q): If G is not bipartite, then not every subgraph of G is bipartite. (True: equivalent to the previous.)
2. By hypothesis, let T be a tree, meaning that T is connected and has no cycles. Since T contains no cycles at all, it contains no cycles of odd length. Hence the Bipartite Graph Theorem (GN I.11 in the Notes) says that T is bipartite, which is the desired conclusion.
3. A theorem is usually stated in the form "If A then B" or "All A's are also B's". The converse statement is "If B then A" or "All B's are also A's". The converse might well be false, even if the original statement is true.
In this case, the original true statement is "All trees are also bipartite graphs", and its converse is "All bipartite graphs are also trees". This is indeed false: for example C4 is a bipartite graph, but not a tree.
4. Proof: By hypothesis, consider tree T (connected and acyclic) and a vertex v with d neighbors w1,..., wd. Extend the edge vw1 into a path as long as possible: P1 = vw1x1...y1z1. Then I claim z1 is a leaf of T. Indeed, if z1 had any neighbor t ≠ y1, then we could extend P1 further unless t were already used in the path: P1 = vw1x1...t...y1z1. But this would mean that T has the cycle C = t...y1z1t = tPz1t, which is impossible since T is acyclic. Hence z1 does not have any neighbor other than y1, so deg(z1) = 1, and z1 is a leaf.
Similarly, we produce leaves z1,...,zd from w1,...,wd. If two of these were the same, z = zi = zj, we would get the cycle:
5a. Let G be an acyclic graph, and write its connected components (GN I.7): G = T1 ∪...∪ Tk. By defintion each Ti is connected, and cannot have any cycles since G has none. Since it is connected and acyclic, the component Ti is a tree, so G is a disconnected union of trees, and hence a forest.
5b. Consider the forest G = T1 ∪...∪ Tk with the component trees Ti having ni vertices and ni−1 edges (GN II.4), so that n = n1 + ... + nk. Then the total of edges in G is:
- Prove: In a tree T, the average degree of a vertex is always less than 2.
Example: Let T be the star-tree with vertices v1, v2,..., v10 and edges ei = v1vi for i = 2,3,...,10. This T has one vertex with degree 9 and 9 vertices with degree 1, so the average is 1⁄10(9 + (9)(1)) = 18⁄10 < 2.
Note: An example is not part of a proof, but can help you understand what the statement says, and how to find a proof. - Prove: T is a tree ⇔ T contains a unique path between each pair of vertices.
2. (⇒) Assume T is a tree (connected and acyclic). Then any vertices x,y have some path P between them (since T connected).
Now suppose for a contradiction that there is a different path Q from x to y. (It does not follow that xPyQx is a cycle, since P and Q might cross each other several times, which is not allowed in a cycle.)
Let v be the last vertex before P and Q diverge (for example v = x if their first steps are different). Let w be the first vertex after v where P and Q cross (for example w = y if they do not cross until their endpoint). Then vPw and vQw (the parts of P and Q between v and w) are disinct paths which do not cross except at their common endpoints, so C = vPwQv is a cycle. This contradicts the assumption that T is acyclic.
Supposing two distinct P and Q leads to a contradiction, so the path P must be unique.
(⇐) Assume T has a unique path between any two vertices. Then T is connected (since there is some path). Suppose for a contradiction that T had a cycle C = xy....zx. Then P = xy and Q = xz...y are distinct paths from x to y, but this is impossible since T has unique paths. Thus there cannot be a cycle in T, so T is acyclic and connected, so T is a tree.
HW: Finish the Hand-in Proofs due 3/28.
- Cayley's Theorem says there are nn−2 trees on vertices V = {1,2,...,n}. Explain how the existence of Prufer's Transformation proves Cayley's Theorem. Not how does the transformation work, but rather, given that the transformation works, why does Cayley's Theorem follow?
- Trees with n = 4 vertices.
- For each of the 16 trees T with n = 4 vertices, use the algorithm to construct its Prufer sequence σ = (s1, s2).
- For each sequence σ = (s1, s2) with si ∈ {1,2,3,4}, compute the Reverse Prufer Transformation Rev(s), which produces a 4-vertex tree. Verify that this is the inverse of the mapping in (a).
- HHM p.51 #2: Find the Prufer sequence σ of each tree pictured:
- HHM p.51 #3: Find the tree T corresponding to the sequence σ = (5,4,3,5,4,3,5,4,3).
- HHM p.51 #1: Explain why the sequence s will never contain the leaf vertices of T. More generally, each vertex v in T will appear deg(v)−1 times, where deg(v) is the number of edges connected to v in T.
- Special Prufer sequences
- Let c be a whole number. What tree T corresponds to the Prufer sequence σ = (c,c,...,c) of length n−2 ? Hint: Do the reverse Prufer transformation on some examples.
- Let σ be a sequence of n−2 distinct numbers between 1 and n. What kind of tree corresponds to σ? Hint: Try examples.
- Extra Credit: Find the number of trees on n = 6 vertices by elementary means (not Prufer's Transformation). One way is to draw all the possible shapes of unlabeled trees with 6 vertices (e.g. the path and the star, but these are not all). Then figure out how many distinct trees can be made by labeling the vertices with 1,...,6.
(The symmetry of the unlabeled tree will be relevant.)
Do this also for n = 7, and as high as you can. Find other, clever ways of doing it, perhaps even finding your own proof of Cayley's Theorem.
Note: The number of unlabeled trees (i.e. shapes of trees) for n = 3,4,...,10 is: 1,2,3,6,11,23,47,106. This is itself a fascinating, very difficult sequence. - Extra Credit: Consider the distinct trees on n unlabeled vertices: these are the possible "shapes" for labeled trees. Find the number of shapes explicitly for n ≤ 10. Describe your method of generating all possible shapes, and ensuring you don't double-count different drawings of the same graph.
- Extra Credit: If T has d leaves, then σ contains exactly n−d distinct entries, and vice versa. Use this to give a formula for the number of trees with n vertices and d leaves. (Recall examples n = 6, 8; d= n−3, n−4.)
2a & b. The table shows all trees and their Prufer sequences:
| 1−2−3−4 | 1−2−4−3 | 1−3−2−4 | 1−3−4−2 | 1−4−2−3 | 1−4−3−2 | 2−1−3−4 | 2−1−4−3 | 2−3−1−4 | 2−4−1−3 | 3−1−2−4 | 3−2−1−4 | ||||||||||||
| (2,3) | (2,4) | (3,2) | (3,4) | (4,2) | (4,3) | (1,3) | (1,4) | (3,1) | (4,1) | (1,2) | (2,1) |
| 3 | 3 | 2 | 2 | ||||||
| | | | | | | | | ||||||
| 2−−1−−4 | 1−−2−−4 | 1−−3−−4 | 1−−4−−3 | ||||||
| (1,1) | (2,2) | (3,3) | (4,4) |
Performing the Reverse Prufer Transform on each sequence σ recovers the tree above it.
3. First tree: σ = (2,2,1,3,1,4,4,1,5). Second tree: (5,8,4,3,3,3,9)
4. The Reverse Prufer Transformation on σ = (5,4,3,5,4,3,5,4,3) goes like this:
| Vi\ σi | 1,2,6,7,8,9,10,11 | 2,6,7,8,9,10,11 | 6,7,8,9,10,11 | 7,8,9,10,11 | 8,9,10,11 | 9,10,11 | 10,11 | 5,11 | 4,11 |
| si | 5 | 4 | 3 | 5 | 4 | 3 | 5 | 4 | 3 |
| ℓi | 1 | 2 | 6 | 7 | 8 | 9 | 10 | 5 | 4 |
The left-over vertices are V10 = {1,2,...,11} \ {ℓ1,...,ℓ9} = {3, 11}. Putting together the edges ℓi−−si and 3−−11, we get the tree:
| 1 | 2 | 6 | |||||||
| | | | | | | |||||||
| 7 | −− | 5 | −− | 4 | −− | 3 | −− | 11 | |
| | | | | | | |||||||
| 10 | 8 | 9 |
5. The leaf vertices of T will be pulled off in the course of the Prufer Transformation, which records their neighbors as si in σ. The leaves themselves will never be neighbors of leaves, so they are not in σ. Furthermore, a vertex v with k neighbors will have k−1 of them pulled off (recording si = v each time), and then v becomes a leaf itself and is eventually pulled off, or it is left over at the end. Either way, v appears k−1 times in σ.
6a. Recall that for any T, each v ∈ T appears deg(v)−1 times in σ. Since c appears n−2 times in σ, the vertex c in T must have deg(c) = n−1 neighbors. This means c is a central vertex with an edge to every other vertex, and T is a star tree.
6b. Since the n−2 entries appear once each, they correspond to vertices in T of degree 2. The 2 vertices which do not appear are the leaves of T. Hence, T has no branching (degree 3 or more), and T must be an n-vertex path.
HW: Give careful proofs of the two statements below, using the Graph Notes I and II.1-II.5 below.
- Proposition:If T is a tree, then T−e is disconnected for any edge e ∈ T. ( Here T−e means remove the edge e, but leave its end vertices.)
- Proposition: If T is a tree, then T+e has a cycle for any edge e ∉ T. (That is, e = xy where T has no edge between x and y.)
- Start with the hypothesis (what is assumed in the proposition) and end with the conclusion (what is to be deduced).
- State and use the definitions of the terms used, from the Graph Notes.
- Make a chain of logical deductions from the hypothesis and definitions, possibly using previous results up to Graph Notes II.5, all the way to the conclusion.
- Use suggestive pictures, but also describe their content in words and formulas to make sure you have covered every possible case.
- Do not automatically try proof by induction. Work directly from the definitions, making your reasoning flow from hypothesis to conclusion.
- Another method is proof by contradicition. Assume the hypothesis is true and the conclusion is false, and derive a contradiction (a statement that would be both true and false under the assumptions). This cannot hold, so the conclusion must be true whenever the hypothesis is.
HW:
- Consider the six graphs in
HHM p. 76, Fig. 1.77.
- Check Euler's Formula for these graphs:
n − q + r = 2,
where n is the number of vertices, q the number of edges, and r the number of connected regions of the plane cut out by the drawing. - Show that two of the graphs are different plane drawings of the same graph. (It is easy to identify the two candidates.) That is, label the vertices appropriately to give edges between the same vertices for both graphs. It is not clear that the regions also match, but check that nevetheless both have the same number of regions.
- Check Euler's Formula for these graphs:
n − q + r = 2,
- The octahedron is a solid which consists of two four-sided pyramids stuck together bottom-to-bottom:
Show that this graph is planar: i.e. find a different drawing, without edge crossings, and check Euler's Formula. Hint: Imagine putting your eye close up to one of the faces, so that you see it as a triangular frame with the rest of the egdes inside. - Induction to prove Euler's Formula. Draw your own planar graph G, and identify a set of edges {e1,..., ek} which, when removed, leave the graph connected but break all the cycles in G: that is, T = G − {e1,..., ek} is a tree. (Note: G − e means removing the edge e but leaving its end-vertices.)
Now, start with T and add back the edges e1,..., ek, and see what happens to n,q,r in each step. Explain why Euler's quantity n − q + r does not change. - Connected and non-connected graphs
- Draw some connected planar graphs of your own (no edges crossing), find the number of vertices, edges and regions (n,q,r) and verify that n − q + r = 2.
- Find examples showing the formula does not work if the graph is not connected.
- Find and prove the correct generalization of Euler's formula for a non-connected graph with k connected components. Hint: n − q + r is the same for any graph with k components. You can show this by the same inductive procedure as for connected graphs, starting with a forest of k trees.
- Suppose G is a connected planar graph with 24 vertices, and it is regular of degree 3.
How many regions must there be in any planar drawing of G?
Extra Credit: Construct such a graph.
1b. The only two of the six graphs which have the same number of vertices are the lower left and middle right (8 vertices each). Start by labeling the two vertices of degree 2 as A,B in each graph, then label their neighbors C,D, etc. The result is two graphs with the same vertices and edges, just drawn differently.
2. See p. 82:
3. G0 = T is a tree, having n vertices, q = n−1 edges, and r = 1 region, giving n − q + r = n − (n−1) + 1 = 2. Adding an edge to T creates a cycle which cuts off a finite region from the infinite region; so T+e has n vertices, q = n edges, r = 2 regions, giving n − q + r = n − n + 2 = 2. Adding another edge cuts one more region in two, giving q = n + 1, r = 3, and still n − q + r = 2. Continuing in this way, after each new edge the new values of (n,q,r) become (n', q', r') = (n, q+1, r+1), and the quantity n' − q' + r' = n − q + r remains unchanged, namely 2. This is the idea behind the inductive proof of Euler's Theorem in the next lecture.
4c. Proposition: If G is a planar graph with k connected components, n vertices, q edges, r regions, then:
n − q + r = k + 1.
Proof: If a component Gi is drawn in the plane with ni vertices, qi edges, and ri regions, then the original Euler formula applies to this connected graph: ni − qi + ri = 2. A drawing of G is just placing G1,...,Gk next to each other: none of the vertices, edges, or regions overlap, except that the infinite region is the same for all G1,...,Gk. Thus:
= ∑i (ni − qi + ri) − k + 1 = 2k − k + 1 = k + 1.
5. We have G with n = |V| = 24, and deg(v) = 3 for all v, so q = |E| = ½∑v∈V deg(v) = ½(24)(3) = 36. Hence r = 2 − n + q = 2 − 24 + 36 = 14.
HW:
- In class we proved Euler's Formula (for connected planar graphs) and the Edge-Region Inequality (for any planar):
n − q + r = 2 and gr ≤ 2q, where n, q, r are the numbers of vertices, edges, and regions; and the girth g is the length of the shortest cycle. We showed that the complete graph G = K3,3 is not planar by contradiction.
Specifically, assume a planar drawing of G, so that Euler's Formula and the Edge-Region Inequality would apply. We directly count n, q, and g for G, and compute r = 2 − n + q; and finally we find that the Region-Edge Inequality does not hold. This contradicition shows our assumption that G is planar must be false. (In fact, ∑ deg(R) would have to be a number greater than gr = 20, and less than 2q = 18.)- Do the above argument for G = K5, the complete graph on 5 vertices.
- Apply the argument to a general complete graph Kn. For which n does this satisfy the Euler Formula and the Edge-Region Inequality? Which Kn's are planar?
- Extra Credit: Do the same for a general complete bipartite graph Ks,t with n = s+t vertices. Which of these are planar?
- Planarity tests
- Consider the graph G which is produced from K5 by subdividing one edge e = xy into a path P = xzy. (That is, we insert an extra vertex z in the middle of edge e.) Try to show G is non-planar by the same strategy as for K5: that is, assume it is planar and compute the region number r from Euler's Formula; then check the Region-Edge Inequality.
- Do the same for a one-vertex subdivison of K3,3.
- If the Inequality does hold for these graphs, does that mean they are planar? Hint: Show that planar drawings of these graphs would lead to planar drawings of K5 and K3,3.
- Maximal planar graphs.
- If G is connected planar with at least 3 vertices, and having cycles, then its girth g ≥ 3.
Use this, together with Edge-Region Inequality and Euler's Formula to show that:
q ≤ 3n − 6. Show that this inequality holds even if G is planar with at least 3 vertices, but has no cycles or is disconnected. - We say a planar graph G is maximal planar if it has the largest possible number of edges, given n vertices: q = 3n−6. See Graph Notes III.7 and HHM Thm 1.33, p. 78.
Question: Which Kn's are maximal planar? - Which of the Platonic graphs on p. 82 are maximal planar? How could you tell without counting the vertices and edges, only looking at the regions?
- If G is connected planar with at least 3 vertices, and having cycles, then its girth g ≥ 3.
Use this, together with Edge-Region Inequality and Euler's Formula to show that:
- Extra Credit: Draw a 3-regular planar graph with n vertices, for any n = 2k ≥ 4. Say as much as you can about regular planar graphs with any values of n and d. For which n,d does such a graph exist? How unique are they?
- Extra Credit: We know that a planar G is maximal planar whenever q = 3n−6, or equivalently if all its regions have deg(R) = 3 boundary edges.
Use computations with the edge-number q, along with Kuratowski's Theorem, to examine the following:
- There are no complete bipartite graphs Kn1n2 which are maximal planar.
- The complete multi-partite graphs G = Kn1...nk are defined by splitting V into k disjoint sets V1,..., Vk of sizes n1,..., nk with each vertex in Vi having an edge to every vertex in the other Vj for j ≠ i. Compute the number of edges of G. Find all the G of this form which are planar and/or maximal planar.
Minimal forbidden: K5 = K11111, K33, K123 ⊃ K33, K1122 ⊃ TK5, K1113 ⊃ TK33. Remaining: K1t for t ≥ 1; K2t for t ≥ 2; K11t for t ≥ 1 (sub bipyramid); and K1, K2 = K11, K3 = K111, K4 = K1111 (tetrahedron), K122, K222 (octahedron), K1112 ⊂ K23.
1b. For G = K1 and K2, we have g = 0, so the Region-Edge Inequality is automatically satisfied. Indeed, in these cases, the graph is obviously planar.
For G = Kn with n ≥ 3, we have q = (n | 2) = ½n(n−1), g = 3, so if planar then r = 2 − n + ( ½n2 − ½n) = ½n2 − 3⁄2n + 2. The edge inequality becomes:
2a. For K5 with an extra vertex on one edge, we have n = 6, q = 11, g = 3. If planar, we have r = 2 − 6 + 11 = 7 and gr = (3)(7) = 21, 2q = (2)(11) = 22, so the Region-Edge Inequality holds. Thus we get no contradiction. However, this failed proof does not mean G is planar: the jury is still out, and other arguments might succeed.
2b. For K3,3 with an extra vertex on one edge, we have n = 7, q = 10, g = 4. If planar, we have r = 2 − 7 + 10 = 5 and gr = (4)(5) = 20, 2q = (2)(10) = 20, so the Region-Edge Inequality holds, and again there is no contradiction.
2c. Neither of these graphs is planar. If we had any planar drawing of either, we could erase the extra vertex (turning the subdivided edge back into a single edge), and get a planar drawing of K5 or K3,3. Since we know this is impossible, we could not have any planar drawing of the subdivided graphs.
3a. Since 3 ≤ g, the Edge-Region Inequality gives: 3r ≤ gr ≤ 2q. But since G is connected, we have r = 2 − n + q, so that 3(2 − n + q) ≤ 2q. Solving for q gives: q ≤ 3n − 6.
Now if G, with q edges, is disconnected or has no cycles, then we can draw extra edges to connect all the components and to produce cycles, giving a graph G' with q' edges. Then q' ≤ q ≤ 3n − 6.
3b. Kn has q = ½n(n−1), which is maximal planar if ½n(n−1) = 3n−6. Solving gives n = 3,4, which are indeed maximal planar: K3 is a triangle, and K4 can be drawn as a triangle with a vertex in its center and an edge to each corner.
3c. If a graph has any regions with 4 or more edges, then we can draw an extra edge across the region, without causing any edge-crossings. In fact the maximal planar graphs are precisely those having only triangular regions (including the infinite region). Here triangular means 3 boundary edges, which may be drawn as curves.
HW:
- Planar drawings
- Let G = K5 − e ; that is, remove any edge from the complete graph on 5 vertices. It is clear that this G cannot contain a subdivision of K5 or K3,3, so Kuratowski's Theorem guarantees that G is planar. Make a proper plane drawing of G (i.e. no edges crossing).
- Do the same for G = K3,3 − e.
- Extra Credit: Make the above drawings with straight-line edges only.
- Kuratowski's Theorem gives a complete criterion for planarity: G is planar if and only if G does not contain any forbidden subgraph, a subdivision of K5 or K3,3. For each of the following non-planar graphs, find a forbidden subgraph.
Example: To give a subdivision of K3,3, inside G, mark two triples of vertices in G (3 "plus vertices" and 3 "minus vertices"), and for each plus and minus pair, find a path connecting them in G, so that the 9 paths do not intersect each other (except at common endpoints). Then if you could find a planar drawing of G, you could do the same for the included subdivison of K3,3,, and hence for K3,3, itself, which is impossible. Hence G is non-planar.- G = Cub3 + e, the 3-dimensional
cube graph with one extra edge e between opposite corners of the cube: e = xy for vertices x = 000 and y = 111.
- G is the 10-vertex Petersen graph on HHM p. 65:
- G is the 6-vertex graph from class:
- Extra Credit: G is the 4-dimensional cube graph Cub4 from HW 3/14 #3b. I think it has both K5 and K3,3 subdivisions.
- G = Cub3 + e, the 3-dimensional
cube graph with one extra edge e between opposite corners of the cube: e = xy for vertices x = 000 and y = 111.
- Extra Credit: Use Kuratowski's Theorem to list (or at least count) all the non-planar graphs with 6 vertices. (Assume the vertices are unlabeled, so we are only interested in the "shape" of the graph.)
- Planarity criteria. For each statement below, give its converse statement, and determine whether this converse is true.
If true, give a reference in the Graph Notes; if false, give a counter-example.
As usual, we assume G is a graph with n vertices, q edges, and girth g.- If G is connected and planar, then gr ≤ 2q (where we define r = 2−n+q).
- If G is planar, then q ≤ 3n−6.
- If G is planar, then G contains no subdivision of K5 or K3,3.
2a. This graph cannot contain a subdivision of K5, since it does not have 5 vertices of degree 4, only 2 such vertices. But in the following diagram, the square and circle vertices can be taken as the two sides of a subdivision of K3,3, with two extra edges (broken lines).
2b. Again, this graph cannot contain a K5 subdivision, since all its vertices have degree 3. The figure shows a subdivision of K3,3 inside G: there are 3 red and 3 blue vertices, connected by 9 gray paths having no common vertices except endpoints. There is also an extra vertex, not part of K3,3, with its edges drawn as broken lines.
2c. The graph contains both a subdivision of K5 along with an extra edge (broken line), and a copy of K3,3 along with extra edges.
X. Kuratowski says we get all non-planar graphs from K5 and K3,3 by subdividing edges into paths, and then adding extra vertices and edges. We can get 6 vertices in 3 ways:
- G = K5 + v + E', meaning do no subdivision, but add one outside vertex v, along with any set of edges E' connecting v to some vertices of K5. This gives 6 different unlabeled graphs, depending on |E'| = 0,1,...,5, which are all those having an undivided K5 subgraph.
- Let G be K5 with one edge e = xy subdivided into a path xzy, and then add edges connecting z to 0,1,2 vertices, giving 3 distinct unlabeled graphs. (If we connect z to all 3 of the original vertices, we get one of the graphs of the previous type.)
- G = K3,3 itself, with any possible extra edges: we can put 0,1,2, or 3 edges among each triple, giving 42 graphs. Except that if all 3 on 1 side have edges, then there can be no edges on the other side, since this would lead to a K5 subgraph: thus only 32 + 2. But this must be divided by the symmetry between the triples (excluding the 3 cases which are already symmetric) so we have a total of ½(32 + 2 − 3) + 3 = 7 distinct unlabeled graphs.
Final answer: There are 6 + 3 + 7 = 16 distinct unlabeled non-planar graphs on 6 vertices.
4a. Statement: If a graph G has gr ≤ 2q (where we define r = 2−n+q), then G is planar.
This is false for G = K5 + v + e, meaning the complete graph K5 together with an extra vertex v and an edge e to one of the previous 5 vertices. This is connected with n = 7, q = (5 | 2) + 1 = 11, r = 2−n+q = 6, g = 3, and the inequality gr = 18 ≤ 2q = 22 is valid. However, G is not planar, since it contains K5. This illustrates that gr ≤ 2q is a necessary condition for G to be planar, but not a sufficient condition.
4b. Statement: If a graph G has q ≤ 3n−6, then G is planar.
Again this is false, with the same counter-example: q = 11 ≤ 3n−6 = 12. Again the condition is necessary, but not sufficient.
4c. Statement: If a graph G contains no subdivision of K5 or K3,3, then G is planar.
This is true, and is one direction of Kuratowski's Theorem, Graph Notes III.7
XX. Graph Notes III.5 gives three conditions (a), (b), (c), any of which defines a maximal planar graph. To show their logical equivalence, prove the following implications for any graph G with n ≥ 3 vertices:
- (a) ⇒ (b): If G has n vertices, 3n−6 edges, then adding any extra edge e will make G+e non-planar.
- (b) ⇒ (c): If G+e is non-planar for any e ∉ G, then all regions R of G are triangles: deg(R) = 3.
- (c) ⇒ (a): If deg(R) = 3 for all regions R, then G has n vertices, 3n−6 edges.
XX. (b) ⇒ (c): If G+e is non-planar for any new edge G, and G had a region with deg(R) ≥ 4 edges, then we could connect one of the 4 vertices to another vertex diagonal from it, leaving G+e planar. This contradicts the hypothesis, so the assumption that deg(R) ≥ 4 must be false, and we must have deg(R) ≤ 3. But only the infinite region of K1 or K2 can have deg(R) < 3, and our n ≥ 3, so deg(R) = 3.
XX. (c) ⇒ (a): If every region is a triangle, deg(R) = 3, then each edge has 2 different regions on its two sides, and the proof of the Edge-Region Inequality simplifies to give the equality: 3r = ∑R deg(R) = 2q. That is, 3(2 − n + q) = 2q, or q = 3n−6.
HW:
- We define polyhedron graphs in Graph Notes IV.1−2.
Theorem: Any polyhedron graph has at least one face with deg(R) ≤ 5. Thus, any polyhedron must have a face which is a pentagon or simpler polygon.
This is analogous to Graph Notes III.8, where we prove that any planar graph has at least one vertex with deg(v) ≤ 5. Thus the above Theorem is an example of duality in polyhedral graphs: any result about vertices has a corresponding result about regions.- Imitate the proof in GN III.8 to prove the above Theorem. That is, use the facts in GN IV.3 to establish q ≤ 3r−6. Compute the average of the deg(R)'s using the Edge-Region Inequality, finding it is < 6. Conclude that there must be some region with deg(R) ≤ 5.
- Extra Credit: Try to find a planar graph which has as few as possible vertices or regions of degree 5 or less. Ideally, give a family of planar graphs, getting larger and larger, but each with only one (or few) vertices of deg(v) ≤ 5. I do not know an answer to this question.
- For each of the following solids, check the Euler formula: #corners − #edges + #faces = 2; then give a planar drawing of its edge-graph.
- Twisted drum with a hexagon on top, a slightly rotated hexagon on the bottom, and 12 triangles joining them.
- A pyramid with three triangular sides and a triangular bottom: this is called the tetrahedron (Greek tetra = four)
- The tetrahedron with all 4 corners sliced off to form small triangles. Hint: Modify your previous planar drawing of the tetrahedron. What effect does silicing off corners have on the vertices of the graph?
- The tetrahedron with 4 corners sliced off, and also each of the 6 original edges shaved off to form long, thin rectangles. This shape is called the permutahedron: it has a face (hexagonal or rectangular) for each vertex, edge, and face of the original tetrahedron.
- Cube with all 8 corners cut off to form small triangles. Hint: modify the usual planar drawing of the cube.
- Cuboctahedron, which is a cube with a cut taken off each corner, large enough so the triangular faces touch:
- Extra Credit: Describe the dual polyhedra and dual edge-graphs of the above solids.
- Extra Credit: The permutahedron has its name because it can be constructed in 4-dimensional space by starting with the corner (1,2,3,4) and permuting (switching around) the coordinates in every possible way, giving 24 corners in all.
Edges correspond to line segments between pairs of vertices related by switching just one pair of coordinates, like (1,2,3,4)−−(1,3,2,4).- Construct a 3-dimensional paper model of this polyhedron.
- All the vertices, and hence the entire polyhedron, is contained in the 3-dimensional plane in R4 defined as the points (x,y,z,w) with x + y + z + w = 10. Find an orthonormal basis of this 3-space (a set of orthogonal axes), and compute the 3 coordinates of each corner point. These can be used to construct the permutahedron in 3-spcace, ideally to compute the inequalities defining the faces.
- Show that the permutahedron is obtained by slicing off (truncating) the corners of the octahedron.
- Extra Credit Project: Graph duality. For a planar graph G, we get the dual graph G^ as follows. For each region R of G, we draw a vertex v^ of G^ in the center of R; and for each pair of adjacent regions R1, R2 of G, we draw an edge e^ = v1^−−v2^ of G^.
- Experiment with examples of G^ for polyhedron graphs, and conclude that G^ is also a polyhedron graph. In fact, if G is the edge graph of a polyhedron P, then G^ is the edge graph of the dual polyhedron P^ with one corner in the center of each face of P.
- Vertex-truncation of a polyhedron means to slice a bit off a corner v, exposing a new face F with deg(F) = deg(v). Stellation means to introduce a new vertex v slightly outside a face F, with new edges from v to the vertices of F, and new triangles from v to the edges of F, so that deg(v) = deg(F). Show that vertex-truncation and stellation are dual to each other: that is, the dual of the a vertex-truncation of P is a stellation of P^, and vice-versa.
- Now experiment with G^ for more general planar graphs, say for G maximal planar, a cycle, a path, or any tree. Conclude that G^ is not always a graph by our definiton, but a multi-graph allowing multiple edges between two vertices and loop-edges connecting a vertex to itself. Note also that there are choices in how to draw the edges e^, but the results are always different drawings of the same multi-graph.
- Show that if G has n vertices, q edges, r regions, then G^ has n^ = r vertices, q^ = q edges, and r^ = n regions.
- For a region R of G and the corresponding vertex v^ of G^, we have deg(R) = deg(v^).
- The dual of a maximal planar graph G is a 3-regular planar graph G^. Use this to say as much as you can about maximal planar graphs.
- The dual of a dual is the original graph (or multi-graph): (G^)^ = G. Depending on your choices, you may get a different drawing of G.
Thus, the average deg(R) is < 6, meaning some particular deg(R) must also be < 6, meaning deg(R) ≤ 5.
2a. Twisted hexagonal drum: one 6-cycle inside another, with 12 edges zig-zagging between the two cycles.
2b. Tetrahedron: a complete graph K4, most naturally drawn as a triangle with a central vertex connected to each corner.
2c. Vertex-truncated tetrahedron: in the tetrahedron graph, make each vertex grow into a small triangle with the original three edges attached to the corners of the triangle.
2d. Permutahedron: in the previous graph (c), and make each edge grow into a long thin rectangle with the original four edges attached to its corners four corners.
2e. Similar to (c)
2f. Make the triangles in (e) grow until they squeeze out the edges betweem them, leaving only triangle and quadrilateral regions.
- Suppose G is the edge-graph of a Platonic solid. Thus, G is vertex-regular: all vertex degrees are the same deg(v) = d. Also, G is region-regular: all region degrees are the same deg(R) = g.
- Since any polyhedron graph has all deg(v) ≥ 3 with at least one deg(v) ≤ 5; and also all deg(R) ≥ 3 with at least one deg(R) ≤ 5, our Platonic graph must have 3 ≤ d ≤ 5 and 3 ≤ g ≤ 5.
- We have the following formulas for Platonic graphs (GN IV.6, Prob 3 below):
dn = 2q = gr and n − q + r = 2. - Example: (d,g) = (5,3).
- The formulas above become 5n = 2q = 3r, meaning q = 5⁄2 n and r = 5⁄3 n. Solving
2 = n − q + r = (1 − 5⁄2 + 5⁄3)n, we get n = 12, q = 30, r = 20. - Here deg(v) = 5 edges around a vertex means 5 regions between these edges. Also, g = 3 means the every region is a triangle, meaining any region with three boundary edges, curved or straight.
- Draw the outer region as a large triangle, then draw inward using the rule of 5 triangles around each vertex. After a hexagonal shell and a triangular shell, it eventually closes up into a graph with n = 12 vertices, q = 30 edges, and r = 20 triangular regions. There are no combinatorial choices in the growth of this graph, so there is a unique Platonic graph with deg(v) = 5, deg(R) = 3 for all vertices and regions.
- The formulas above become 5n = 2q = 3r, meaning q = 5⁄2 n and r = 5⁄3 n. Solving
- The restrictions 3 ≤ d ≤ 5 and 3 ≤ g ≤ 5 give 9 possible cases.
-
Show that (d,g) = (4,4), (4,5), (5,4), (5,5) are impossible.
Example: Suppose (d,g) = (4,4), meaning 4 squares at each vertex. Then 4n = 2q = 4r and q = 2n, r = n. Thus Euler's Formula works out to: 2 = n − q + r = n − 2n + n = 0. This contradiction means there can be no such graph. Find contradictions for the other cases: the equations might have a solution for n,q,r, but not in positive integers. - Find n, q, r for the remaining five cases (d,g) = (3,3), (3,4), (4,3), (3,5), (5,3).
Note: This computation does not by itself guarantee that there exist such graphs.
-
Show that (d,g) = (4,4), (4,5), (5,4), (5,5) are impossible.
- Do the following parts for each of the five values (d,g) = (3,3), (3,4), (4,3), (3,5), (5,3).
- Construct a unique planar graph with the given data (that is, show there is one and only one way to construct the graph).
- Count the number of vertices, edges, and regions in each planar graph, and match them with the values of n,q,r predicted in the previous problem.
- Look at the pictures of the Platonic solids on HHM p. 82, or the Wikipedia page, each named for its number of faces (in Greek): the tetrahedron (4 faces), the cube = hexahedron (6 faces), the octahedron (8), the dodecahedron (12), and the icosahedron (20). Directly count d,g,n,q,r for each polyhedron, and compare with the corresponding Platonic graph.
- Let (d,g) = (4,3), the octahedron graph.
Illustrate the proof of gr = 2q in this case.
(This is perfectly dual to our old proof of
the Edge Vertex Formula ∑v deg(v) = 2q.)
- Draw the table of the Edge-Region set S = {(e,R) s.t. edge e is on the boundary of region R}. That is, the rows should correspond to the 12 edges, the columns to the 8 regions, and for each pair (e,R) ∈ S you put an × in row e, column R.
- Counting S by columns, see why |S| = ∑R deg(R) = gr.
- Counting S by rows, see why |S| = 2q. Conclude that gr = 2q.
- Extra Credit: Impossible solids
- Explain why we could not produce more Platonic solids by putting 6 triangles around each vertex, or 4 squares, or 3 hexagons, etc. What goes wrong geometrically, i.e. why wouldn't the lengths and angles work? (Compare with #1a above, which asks what goes wrong combinatorially in the construction of the edge-graph.)
- Let (d,g) = (4,4). We showed this case is impossible in 1(a), but try constructing the graph by the same method as 2(a). That is, start with a large outside square, and work inwards using the rule of 4 edges at each vertex and 4 edges around each region. We can keep going like this, producing some sort of graph G, so why isn't it a new Platonic graph?? In fact, this is a peculiar drawing of a very familiar graph which is not a polyhedron graph.
- Extra Credit: Archimedean solid. Does there exist a polyhedron (and/or a polyhedral planar graph) where each vertex is surrounded by 4 edges and 4 regions: 3 squares and 1 triangle? Is there more than one such polyhedron?
Case (d,g) = (3,5): 3n = 2q = 5r, so that q = 3⁄2n , r = 3⁄5n, and 2 = n − q + r = n − 3⁄2n + 3⁄5n = 1⁄10n , and n = 20 , q = 3⁄2n = 30 , r = 3⁄5n = 12.
Similarly for the other cases.
2a. Example: (d,g) = (4,3). The graph has four triangles at each vertex. Starting with a single triangle (vertices 1,2,3, edges 12, 23, 13), we draw two more edges inwards from each vertex (since deg(v)=4). Because each region must have only three edges, these edges must meet up at three new vertices 4,5,6 (edges 14, 42, 25, 53, 36, 63). Finally add edges 45, 56, 64, so that every vertex has four edges, every region (including the outside infinite region) has three boundary edges, and we are done, with no significant choices along the way.
See HHM p. 82 for all the finished graphs.
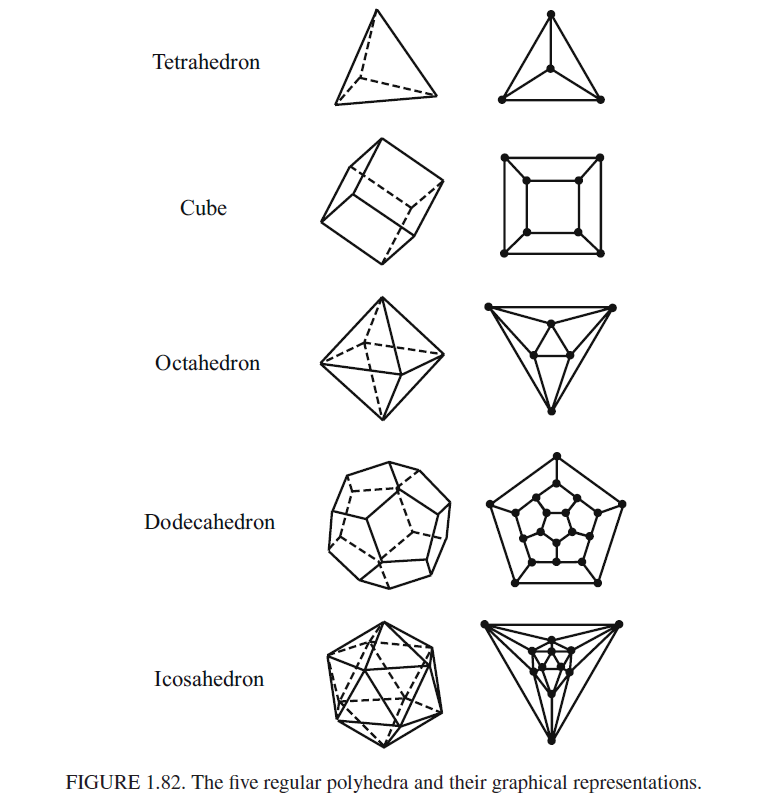
2c. Tetrahedron (d,g) = (3,3), r = 4. Octahedron (4,3), r = 8. Icosahedron (5,3), r = 20. Cube (hexahedron) (3,4), r = 6. Dodecahedron (3,5), r = 12.
Let's examine the octahedron in more detail. It has 4 triangles around each corner, so (d,g) = (4,3). We may label its vertices V = {1,...,6}, where 1 and 6 are the poles and the cycle 23452 is the equator, and we have edges E = {12, 13, 14, 15, 23, 34, 45, 52, 26, 36, 46, 56}. Just as we denote edges by their two endpoints, we may denote regions by their three vertices: R = 123, 134, 145, 125 (the top pyramid) and R = 236, 345, 456, 256 (the bottom pyramid).
To compare this to your graph from 2a, label the graph vertices 1,...,6 so that 1 and 6 are not adjacent and 2345 form a cycle. This gives a direct correspondence between the q = 12 edges of the octahedron and the graph, and between the r = 8 faces of the octahedron and the regions of the graph (remembering to count the infinite region).
3. Using the labeling from Solution 2c above, each pair (e,R) ∈ S is marked with an ×. Each edge e = ab is on the boundary of any region whose vertices include a,b.
| e \ R | 123 | 134 | 145 | 125 | 236 | 346 | 456 | 256 |
| 12 | × | × | ||||||
| 13 | × | × | ||||||
| 14 | × | × | ||||||
| 15 | × | × | ||||||
| 23 | × | × | ||||||
| 34 | × | × | ||||||
| 45 | × | × | ||||||
| 25 | × | × | ||||||
| 26 | × | × | ||||||
| 36 | × | × | ||||||
| 46 | × | × | ||||||
| 56 | × | × |
Since each edge e = ab is on the boundary of two regions R = abc and R' = abc', we have 2 ×'s in each row, and the total number of ×'s is: |S| = 2q. Since each region R = abc has g = 3 edges in its boundary, ab and bc and ac, we have 3 ×'s in each column, and the total number of ×'s is: |S| = 3r = gr.
- See Wikipedia articles on the 4-dimensional regular polyhedra:
- Each wire frame drawn in the Wikipedia pages is a 3-dimensional flattening of a 4-dimensional polyhedron, in analogy with the 2-dimensional graphs of 3-dimensional Platonic solids. For example, the 16-cell, an analog of the octahedron, has a drawing with an exterior tetrahedron, an interior tetrahedron in dual position, and a tetrahedral face reaching from each outer vertex to the corresponding inner triangular face.
- Each 4-dimensional solid has a surface consisting of 0-dimensional vertices, 1-dimensional edges, 2-dimensional polygon faces surrounded by edges, and 3-dimensional solid faces surrounded by polygons.
- In the 3-dimensional wire picture, the 3-dimensional faces correspond to the connected regions of space cut out by the polygons, including the infinite region. Each of these (except the infinite region) is the same Platonic solid, somewhat distorted by the flattening.
- We denote the numbers of vertices, edges, polygons, and solids by n,q,r,s respectively. The 4-dimensional polyhedra are named after their number s of 3-dimensional faces: 5-cell, 8-cell, etc.
- Finish the previous assignment, especially HW 4/8 #2.
- 4-dimensional regular polyhedra (Wikipedia pictures)
- Try to visually count the numbers of faces of each dimension, in as many of the 4-dimensional polyhedra as you can.
- Combine these numbers for a given solid to find an analog of Euler's Formula.
- Extra Credit:
For any 4-dimensional regular polyhedron, all its 3-dimensional faces are the same Platonic solid.
Let a be the number of edges around each polygon, b the number of polygons meeting at a vertex of each solid, and c the number of solids meeting at each edge: the triple (a,b,c) is called the Schläfi symbol.
For example, the 4-cube (8-cell) has a = 4 since its polygons are squares, b = 3 squares meeting at a vertex of each 3-cube, and c = 3 cubes meeting around each edge of the 4-cube.
Problem: Find analogs of the Edge-Region and Edge-Vertex formula, and compute the face-numbers n,q,r,s (vertices, edges, polygons, solids) in terms of a,b,c for the six 4-dimensional polyhedra.
- The d-dimensional cube is the set of coordinate points
Cubd = {(x1,..., xd) ∈ Rd with 0 ≤ xi ≤ 1 for i = 1,...,d}.
A k-dimensional face of Cubd, for 0 ≤ k ≤ d−1,
is a set of points in which we fix d−k of the coordinates to be 0 or 1,
and leave the other k coordinates free, producing a copy of a k-dimensional cube inside
Cubd. For example, one of the 2-dimensional faces of Cub4 is: {(1, x2, 0, x4) with 0 ≤ xi ≤ 1 for
i = 2,4}.
- Determine the number of k-dimensional faces of Cubd .
- Combine the numbers from part (a) to find an analog of Euler's Formula.
- Extra Credit: One family of higher-dimensional regular polyhedra is the analog of the equilateral triangle and the tetrahedron, called the d-simplex. Its corners are any d+1 points in Rd having distance 1 between each pair. We can also take these points to be the coordinate vectors (unit vectors along each axis) in (d+1)-dimensional space. Find equations and inequalities which cut out the d-simplex in Rd+1; determine its number of faces of each dimension; and check the Euler Formula.
n − q + r − s = 0.
We call the right-hand side the Euler characteristic of the 4-dimensional shape. More precisely, the Euler characteristic of the hollow shell of a convex 3-dimensional polyhedron is n − q + r = 2; and for the hollow 3-dimensional shell of a 4-dimensional convex polyhedron, it is n − q + r − s = 0.
3a. The number of k-dimensional cubic faces of the d-dimensional cube is: fk = 2d−k (d | d−k) = 2d−k (d | k).
3b. The Euler characteristic of the (hollow) d-cube is:
f0 − f1 + f2 − ... + (−1)d−1 fd−1 = ∑k=0 d−1 (−1)k2d−k (d | k).
- We defined a k-coloring of a graph G to be a mapping c which gives each vertex v ∈ V a color c(v) in some allowed set of k colors. This is a proper k-coloring if no two neighbors have the same color: c(v) ≠ c(w) whenever e = vw ∈ E.
- A graph is bipartite if and only if it has a proper 2-coloring: we can take the labels + and − on the vertices as 2 colors.
- The chromatic number χ(G) is the minimum number of colors k in a proper coloring. For example, an odd cycle like C5 has χ(C5) = 3, since it is easy to find a 3-coloring, but a 2-coloring is impossible since the graph is not bipartite.
- The Greedy Algorithm (GN V.6) gives a proper coloring of any graph G. You choose an arbitrary order for the vertices, then color them one by one, always using the smallest color that does not conflict with previous vertex colors. (This assumes the colors are numbered, color #1, #2,...)
- Applications of graph coloring
- HHM p. 87 #2. Scheduling committees.
- HHM p. 87 #3. Separating trouble-makers.
- For each of the graphs below do the following:
- Find the maximum vertex degree Δ(G) = max{deg(v) for v∈V}.
- Find a proper coloring using the Greedy Algorithm with some ordering of the vertices. Use numbers 1,2,3,... for the colors (but realize that these have no relation to the numbering of the vertices v1,..., vn). If your coloring uses only k colors, then a minimal coloring is no worse: χ(G) ≤ k. If you think your coloring is not minimal, change the order of vertices and repeat the Greedy Algorithm.
- As you construct your Greedy colorings, explain why no step uses colors higher than Δ(G)+1, which means χ(G) ≤ Δ(G)+1.
- To prove your coloring is minimal, give a reason why fewer colors are impossible. For example, us GN V.2, 4, or 8. This will determine χ(G) exactly.
- Cycle Cn
- Path Pn
- Star graph K1,m (a complete bipartite graph)
- Make up your own tree T
- Complete graphs Kn
- Complete bipartite graphs Kr,s
- The graph G with V = {v1,...,v6} and E = {v1v4, v2v3, v3v6, v4v5, v5v6}
- Extra Credit: The graphs of regular polyhedra on p. 82.
- Extra Credit: The 4-dimensional cube Cub4 from HW 10/28.
- Show that if Δ(G) is the maximum of the vertex-degrees of G, then the Greedy Algorithm always constructs a coloring with at most Δ(G) + 1 colors. Conclude that χ(G) ≤ Δ(G) + 1, which you checked for the examples above.
- Consider this US map. Let G be the dual graph, with vertices corresponding to states, and edges to pairs of states which share a border (not just a corner).
- Mark a proper 4-coloring on the map, so that no two adjacent states have the same color (i.e. a proper 4-coloring of G). Thus, χ(G) ≤ 4.
- Show that no 3-coloring is possible. Thus, χ(G) ≥ 4. Hint: Look at the states around Nevada, or around Tennessee.
1b. Make a graph G with vertices being the students and edges being the conflicts. An allowed seating arrangement corresponds to a proper coloring of G with the colors being seating areas.
2a. Δ = 2, and the natural ordering of vertices around the cycle gives a minimal coloring. For n even, we use k = 2 colors, which is minimal because we obviously need at least 2 colors: G ⊃ K2 (a single edge), so χ(G) ≥ χ(K2) = 2. For n odd, we use k = 3 colors, which is minimal because G is not bipartite, so χ(G) > 2. At each step, there are no more than Δ = 2 conflicts, so Δ+1 = 3 colors are always enough, but not always minimal.
2b. Δ = 2, and the natural left-to-right ordering gives a minimal coloring, χ(G) = 2: that is, G is bipartite. Again, χ = 2 ≤ Δ+1 = 3.
For G = P4, it is possible to find a bad vertex-order which forces the Greedy Algorithm to use 3 colors (start at the left end, then order the remaining vertices right-to-left). However, any Greedy coloring will use at most Δ+1 = 3 colors, because at any step, there are at most Δ conflicts.
2c. Δ = m, and any vertex-order gives a minimal coloring with χ(G) = 2 colors. In this case, χ(G) is much less than Δ = m.
2d. Any tree T is bipartite, so χ(T) = 2 (unless T has only 1 vertex). Constructing the tree by adding one leaf each time means at most 1 color conflict, so the Greedy coloring has 2 colors and is minimal. In any case, Δ ≥ 1, so 2 ≤ Δ+1.
2e. Δ = n−1, and obviously χ = n, since every vertex conflicts with every other, so they must all have different colors. In this case χ = Δ+1.
2f. Put the smaller vertex set on the left, so that r ≤ s. Then Δ = s, and χ = 2, which is much smaller than Δ+1.
2g. The given vertex order makes the Greedy Algorithm use k = 3 colors, but the graph is just the path P6, which like all trees is bipartite: χ = 2. This illustrates the limitations of Greed. However, a better ordering (coloring the r vertices first, then the s vertices) would lead the Greedy Algorithm to a minimal coloring; but there is no easy way to find such an ordering.
3. Proof. Suppose that in G, a vertex x has m neighbors y1,..., ym, so by definition, m ≤ Δ, the maximum vertex-degree. The Greedy Algorithm chooses c(x) to be the smallest color not conflicting with c(y1),..., c(ym), some of which might not have a color yet. The number of conflicting colors is at most m, so at most Δ, hence there must be a free color in the set {1,2,..., Δ+1}. Continuing in this way, we find that Δ+1 colors are enough for a proper coloring of all the vertices. The minumum number of colors is no larger, so χ(G) ≤ Δ+1.
4b. Recall that the wheel graph Wn+1 means the cycle Cn with each vertex connected to an extra vertex in the middle. The map has 5 states surrounding Nevada, so the dual is a wheel graph H = W6. This has χ(H) = 4 ≤ χ(G), since the 5 states in the rim requre 3 colors, and the middle state forces a 4th color. Since you gave a 4-coloring in part (a), we have χ(G) ≤ 4, and we conclude χ(G) = 4.
HW:
- Let G = Wn, the wheel graph consisting of a cycle Cn−1 (the rim) and an extra vertex in the middle with an edge (a spoke) to every vertex on the cycle.
- Show that χ(G) = 3 if n is odd, χ(G) = 4 if n is even. Hint: To show χ(G) = k, you first show χ(G) ≤ k, usually by explicitly constructing a k-coloring: a minimal coloring is no worse than this. Then show χ(G) ≥ k: here you have to rule out every possible (k−1)-coloring, or show that the graph's structure forces k colors.
- Show that for W6, the wheel with rim C5, the Greedy Algorithm always produces a minimal coloring, regardless of the order of the vertices.
- Now consider W7, with rim C6. Show that the Greedy Algorithm can produce a minimal or non-minimal coloring, depending on the order of the vertices.
- Perform the Greedy Algorithm for the icosahedron graph.
- Use the order of vertices indicated below, and note the bad result: more colors than necessary. (How do you know this is a non-minimal coloring?) Analyze where this algorithm goes wrong.
- The 6-Color Algorithm for planar graphs (Graph Notes VI.2) is just the Greedy Algorithm with a special order of vertices which leads to fewer colors needed.
- Start by choosing vn to be a vertex of minimal degree in G. Then remove vn and choose vn−1 to have minimal degree in the remaining graph G − vn. Continue in this way, taking vi to be a vertex of minimal degree in G − {vi+1,..., vn}.
- Then run the Greedy Algorithm in the opposite direction, successively coloring v1, v2,... with the smallest available color.
- The choice of vertex-order assures that you attach each vi to as few previous neighbors as possible (at most 5), leading to as few color conflicts as possible. In the end, the Algorithm uses at most 5+1 = 6 colors.
- Use the order of vertices indicated below, and note the bad result: more colors than necessary. (How do you know this is a non-minimal coloring?) Analyze where this algorithm goes wrong.
- Consider the following graph G:
- Perform the 5-Color Algorithm on G, with the marked vertex order. (Actually, the Algorithm says to use the efficient vertex-order from the 6-Color Algorithm, but use this order instead.) When you get to a vertex v surrounded by all 5 available colors, switch colors 1 & 3 within the Kempe Chain G13. If that does not free up color 1 for v, use G24 instead to free up color 2.
- There is a Kempe Chain for any pair of distinct colors i ≠ j, so 5×4 = 20 in all. Determine which Gij's work to free up the color i for v.
Hint: In the notation of GN VI.3, the subgraph Gij starts at wi, one of the 5 neighbors of v,with c(wi) = i. We define a new coloring c' by switching colors i and j within Gij, and this frees up the color i for v exactly when Gij ≠ Gji, i.e. when there is no ij-colored path from wi to wj.
- Extra Credit: Shield Graph
- Suppose we try the 5-Color Algorithm with only 4 colors. The trouble is that, as we add the vertices one by one, we cannot avoid connecting a new vertex with 5 previous ones. The Greedy Algorithm gets stuck whenever a new vertex already has 5 neighbors with all the colors 1,2,3,4 (necessarily with one color repeated). This is what happens for the vertex v below, with previous colors marked in red:
In this case, we attempt to free up one of the colors by color-switching in some Kempe Chain.
Show that no possible Kempe chain will free up any of the 4 colors, so the 4-Color Algorithm needs more strategies. Also, find a minimal coloring of this graph by trial-and-error (and show why it is minimal). - Show that the vertex-order below is "efficient", in the sense that each vi has minimal degree in G − {vi+1,..., vn}, meaning this is the kind of order used by the 5- and 6-Color Algorithm.
However, show that the resulting Greedy coloring is not minimal.
- Suppose we try the 5-Color Algorithm with only 4 colors. The trouble is that, as we add the vertices one by one, we cannot avoid connecting a new vertex with 5 previous ones. The Greedy Algorithm gets stuck whenever a new vertex already has 5 neighbors with all the colors 1,2,3,4 (necessarily with one color repeated). This is what happens for the vertex v below, with previous colors marked in red:
- Extra Credit: Look over the "simplified" proof of the 4-Color-Theorem by Robertson-Sanders-Seymour-Thomas, and explain something about the ideas.
- Extra Credit: Minimal colorings can be very subtle and tricky for non-planar graphs. For example, we have seen
that an even wheel-graph like W6 forces χ(G) ≥ 4, but there are many other graphs requiring 4 colors.
Show that each graph below has girth(G) = 4 and χ(G) = 4. (Since girth(G) > 3, there are no possible triangles or wheels.)- The Grotzsch Graph:
- The Chvatal Graph:
- The Grotzsch Graph:
- Extra Credit: Does there exist a maximal planar graph G with n ≥ 4 and χ(G) = 3, or do such graphs always have χ(G) = 4, as is the case for G = K4?
For n even, we argue similarly: it is easy to find a 4-coloring of G, but since the middle vertex is a neighbor of every vertex on the cycle, we have χ(G) ≥ χ(Cn−1) + 1 = 4. Alternatively, we can just quote the Proposition in GN V.7, which is based on the above arguments.
1b. In the Greedy Algorithm under any vertex-order, each new vertex is attached to only 2 others, so that 3 colors are enough, until we attach the center, which might require color 4. After this, each new vertex has degree 3, so that 4 colors are enough. Any Wn with n even has χ = 4, so this is minimal.
1c. For Wn with n odd, if you start by coloring two opposite vertices on the cycle with color 1, the resulting Greedy coloring needs 4 colors, which is no longer minimal.
2a. The Greedy Algorithm needs 5 colors (written in red):
2b. The 6-Color Algorithm gives a vertex-order like the one below, which produces a 4-coloring, and this is minimal since G contains W6.
3a. The Greedy Algorithm uses only 5 colors (shown in red) up to the last vertex v:
3b. The Kempe chain switches in the top (red) coloring which lead to a 5-coloring are: G14, G24, G25, G41, G42, G52. Note that Gij gives a useful color switch exactly when Gij does not contain wj, namely whenever Gij ≠ Gji.
- Problem: Count all possible proper colorings with k available colors. The answer is the chromatic function or chromatic polynomial: pG(k) means the number of proper colorings of the graph G with available colors 1,...,k.
- The chromatic function pG(k) is very different from the chromatic number χ(G), which is the minimum k required for at least one proper coloring. In fact, k = χ(G) is the smallest number with pG(k) > 0, for which there is at least one coloring with k colors.
- Example: The 3-vertex path G = (v1)−−(v2)−−(v3). We count the number of ways to choose vertex-colors c(v1), c(v2), c(v3) from 1,...,k,
with the first two different, and the second two also different (though we could have c(v1) = c(v3)).
A coloring means we choose c(v1) to be any of the k colors, then c(v2) to be any of the k−1 colors different from c(v1), then c(v3) to be any of the k−1 colors different from c(v2). The Product Principle gives:pG(k) = k(k−1)2 = k3 − 2 k2 + k. Note that pG(0) = pG(1) = 0, but pG(2) = 2 > 0, so χ(G) = 2. (Indeed, we know that G, being acyclic, is bipartite.)
- Find pG(k) for the following graphs, using the Product Principle (reduce each object to a sequence of independent choices) and Sum Principle (split the set of objects into disjoint cases).
- Path Pn
- Star graph K1,n−1 (a complete bipartite graph with n vertices)
- Complete graph Kn (Hint: this is one of the Four Basic Problems. Which?)
- The trapezoid graph below:
- G = C4 with vertices v1,...,v4 numbered clockwise.
Hint: Split into two cases: proper colorings c with: (Case 1) c(v1) = c(v3); and (Case 2) c(v1) ≠ c(v3). Use the Product Principle for each case.
- Given a graph H with known pH(k), compute pG(k) for G = H∗v, the graph with an extra vertex v and an edge from v to every vertex of H.
- Wheel graph W5 with a 4-cycle and a central vertex.
- Let G = C3, and use PIE to compute pG(k). Let A be the set of all colorings of the vertices, disregarding edges (no properness condition). Colorings can be non-proper because c(x) = c(y) for any given edge e = xy, so there will be 3 bad sets B1, B2, B3, corresponding to the 3 edges. You must count the bad colorings for each set, and their intersections, and combine by the PIE formula. Your answer should equal #1c above for n = 3 (since C3 = K3).
- Do the same as #2 for G = C4, using PIE to compute pG(k). There will be 4 bad sets corresponding to the 4 edges. You must count the bad colorings for each intersection of the bad sets (24 = 16 terms in all). Your answer should equal #1e above.
- 3-colorings of the n-cycle.
- Let G = Cn for n ≥ 3, and define pn to be the number of proper colorings of G with k = 3 available colors. (This would work for any k, but we take k = 3 for the sake of concreteness.) That is, pn = pG(3) for G = Cn. For example, if n = 3 then G = C3 = K3, so p3 = (3)(2)(1) = 6.
- Also define p2 = (3)(2) = 6, the number of proper 3-colorings of G = K2, and p1 = p0 = 0.
- To evaluate pn, consider two kinds of colorings
- Case 1: c(v1) ≠ c(vn−1). This is equivalent to putting an extra edge between vn-1 and v1, so that a proper coloring would force c(v1) ≠ c(vn−1).
- Case 2: c(v1) = c(vn−1). This is equivalent to pinching vn-1 and v1 into a single vertex, so that a proper coloring of the pinched graph could be un-pinched into a coloring of Cn with c(v1) = c(vn−1)).
- Prove the recurrence:
pn = pn−1 + 2pn−2 for k ≥ 3.
Hint:- Step 1: Start by writing the generating function f(x) = p0 + p1x + p2x2 + ... = ∑k≥0 pkxk, and substitute for pk using the recurrence above, being careful with the first few terms where the recurrence does not apply. Then manipulate the series until you can simplify into expressions involving f(x). Solve the resulting equation to get a simple formula for f(x).
- Step 2: Find the Taylor series of f(x) by partial fractions. The coefficients are the answer.
1c. Basic Problem 2: Count the lists of n distinct items chosen from k. Ans: kn = k(k−1)...(k−n+1).
1d. Coloring vertices from left to right, the Product Principle gives: k(k−1)(k−2)3
1e. Case 1: c(v1) = c(v3). Since there is only one choice for these identical colors, we can regard v1 and v3 as one vertex, so the graph becomes P3, and the number of colorings is k(k−1)2.
Case 2: c(v1) ≠ c(v2). This is pH(k) for the graph H = G + v1v3 with an extra edge, and the Product Principle gives pH(k) = k(k−1)(k−2)2. Final answer: k(k−1)2 + k(k−1)(k−2)2 = k4 − 4k3 + 6k2 − 3k.
1f. First reserve one of the k colors for v, then use the remaining (k−1) colors for H, giving pG = k pH(k−1).
1g. W5 = C4∗v, so:
= k5 − 8k4 + 24k3 − 31k2 + 14k
2. The result of PIE is: k3 − (3 | 1)k2 + (3 | 2)k − (3 | 3)k. This agrees with the result k(k−1)(k−2) in 1c.
3. The result of PIE is: k4 − (4 | 1)k3 + (4 | 2)k2 − (4 | 1)k + (4 | 4)k = (k−1)4 + (k−1). This agrees with the result in 1e.
4. Step 1: We want to solve the Fibonacci-like recurrence pn = pn−1 + 2pn−2 for k ≥ 3, starting from p0 = p1 = 0, p2 = 6.
= 6x2 + ∑n≥3 (pn−1 + 2pn−2)xn
= 6x2 + x ∑n≥3 pn−1xn−1 + 2x2 ∑n≥3 pn−2xn−2
= 6x2 + x (f(x)−p0−p1x) + 2x2 (f(x)−p0) .
4. Step 2: Since the numerator has the same degree as the denominator, the horizontal asymptote is not zero. Evaluate: limx→∞ f(x) = 6⁄−2 = −3. Thus the partial fraction decomposition which matches the horizontal and vertical asymptotes of f(x) will have the form:
- Card Hands.
A deck has 52 cards, 4 suits with 13 cards each. A hand is an unordered collection of 5 cards. Find the number of hands in which all 4 suits appear.
- Do this problem with the Principle of Inclusion-Exclusion. Start with the large, simple set A of all hands, and remove simple bad sets A1,...,A4. Enumerate these sets, and plug into the PIE formula.
- Do this problem in a more straightforward way. Start with the set of all hands, and remove disjoint bad sets, corresponding to hands with exactly 1, 2, or 3 suits appearing.
- Do this problem using the Product Principle, getting a very neat answer.
- Check that all the above answers are the same numerically.
- Find the chromatic polynomial of the following
polyhedron edge-graphs:
- Tetrahedron (triangular pyramid)
- Octahedron (two square pyramids with their bases glued together) Hint: Color the north and south poles first, then the C4 on the equator, using the known pC4(k) from the previous problem set.
- Extra Credit: Cube graph Cub3. (This seems hard.)
- Recall from HW 3/14 #3 that
the d-dimensional cube graph Cubd
has vertices of the form (x1,...,xd),
where each coordinate xi = 0 or 1;
and edges between pairs of vertices
which have only one coordinate changed.
- Use the Basic Problems and Principles to determine vd and qd, the number of vertices and edges of Cubd.
- Cubd can be contructed recursively from 2 copies of Cubd−1 by drawing an edge between each vertex and the corresponding vertex in the other copy. Find a recurrence for vd, and solve it directly, recovering your result from (a).
- Find a recurrence for qd, and solve it by generating functions, recovering your result from (a).
- Given pG(k), use PIE to find an expression for the number of proper colorings which use all the colors {1,...,k}.
- Extra Credit: Conjecture: For subgraphs G1, G2 ⊂ G meeting in a complete subgraph of m vertices, i.e. G1 ∩ G2 = Km, the chromatic polynomial of G is: pG(k) = 1⁄km pG1(k) pG2(k). I can prove this for m = 1 (i.e. a single common vertex), but I am not sure about the general case.
1b. All hands: (52 | 5). Subtract bad hands:
- 5 of one suit: (4 | 1)(13 | 5)
- 4 of one suit, 1 of another suit: 42 (13 | 4) (13 | 1)
- 3 of one suit, 2 of another suit: 42 (13 | 3) (13 | 2)
- 3 of one suit, 1 of another suit, 1 of a third suit: 43/2 (13 | 3) (13 | 1)(13 | 1)
- 2 of one suit, 2 of another suit, 1 of a third suit: 43/2 (13 | 2) (13 | 2)(13 | 1).
1c. Product Priniciple: A good hand must have 2 cards of one suit. Construct all good hands by first choosing which suit has 2 cards, then choosing a set of 2 face-values for that suit, then choosing a list of 3 arbitrary face-values for the remaining 3 suits (listed in order). Answer: (4 | 1) (13 | 2) 133
1d. The answer in each case is 685,464.
2a. The tetrahedron graph is just G = K4, so pG(k) = k(k−1)(k−2)(k−3).
2b. Case 1: Choose two different colors for the poles,
then color the equator C4
with k−2 colors, using pC4(k) = (k−1)4 + (k−1).
This gives
k(k−1)((k−3)4 + (k−3))
colorings.
Case 2: Choose one color for both poles, then color the equator, giving k((k−2)4 + (k−2))
colorings.
Wolfram|Alpha says this simplifies to
pG(k) =
k(k−1)(k−2)(k3 − 9k2 + 29k − 32)
3a. To choose a vertex, make d independent choices of 0 or 1 for each coordinate, giving vd = 2d. For an edge, choose which of the d coordinates is changed, and choose the remaining d−1 coordinates to be 0 or 1: this gives qd = d 2d−1.
3a,b. From vd = 2 vd−1, we recover vd = 2d. From qd = 2qd−1 + 2d for d ≥ 1, we get f(x) = ∑d≥0 qdxd = x⁄(1−2x)2 = ∑d≥0 ((2 | d)) x (2x)d, which gives qd+1 = ((2 | d)) 2d.
4. PIE with A = {proper colorings with k available colors}, Bi = {proper colorings with color i missing} for i = 1,...,k. The number of proper colorings with all k colors is:
- A symmetry of a graph G = (V,E) is a one-to-one mapping of vertices to vertices, σ : V → V, which takes every edge e = xy ∈ E to another edge σ(e) = σ(x)σ(y) ∈ E.
These are more graph symmetries than geometric symmetries, since graphs ignore angles and lengths of edges. Imagine the graph as a collection of thumbtacks (the vertices) pinning down rubber-bands stretched between them (the edges): a graph symmetry is any way to switch around the tacks and rubber-bands into each others' places. - The symmetry group Γ = Sym(G) is the set of all symmetries, endowed with the composition operation: σ o τ = ρ means to do σ after τ, producing a new symmetry ρ. (Note: Γ = Greek letter capital gamma.)
- We have Γ ⊂ Sn, meaning each σ can be writtenas a permutation of vertices 1,...,n, in two-line or cycle notation.
- Example: The star graph G = K1,3 (a complete bipartite graph)
with V = {1,2,3,4}, E = {12, 13, 14}:
In fact, the symmetry group consists of all permutations of the leaf vertices 2,3,4, leaving 1 fixed, so |Γ| = |S3| = 3! = 6. - The set of all colorings of the vertices V with colors numbered 1,...,k is:
C = { all functions c : V → {1,...,k} }, with |C| = kn. These need not be proper colorings: for example, all the vertices could have the same color. - The symmetry class of a coloring c is c = {σ(c) for σ ∈ Γ}; that is, the set of all colorings obtained by moving the graph to itself by a symmetry.
- Counting with symmetry (or up to symmetry) means determining the number of distinct coloring classes. This is |C|, where:
C = {every symmetry class c for c ∈ C}. - Burnside's Formula says:
|C| = 1⁄|Γ| ∑σ∈Γ |Cσ| = 1⁄|Γ| ∑σ∈Γ kcyc(σ).
Here Cσ = {c ∈ C with σ(c) = c} is the set of colorings unchanged (fixed) by σ, and cyc(σ) is the number of cycles of σ as it permutes the vertices of G.
- Burnside's Formula also works with C restricted to the set of proper graph colorings P, where adjacent vertices must have different colors. The proper colorings can also be collected into symmetry classes, and the number of proper colorings up to symmetry is:
|P| = 1⁄|Γ| ∑σ∈Γ |Pσ|,
where Pσ = {c ∈ P with σ(c) = c} is the set of proper colorings unchanged by σ. There is now no easy formula for |Pσ|, but it can ususally be found similarly to |P| = pG(k).
- Find the symmetry groups of the following graphs G, writing each element π ∈ Γ = Sym(G) in cycle notation.
- E4, an empty graph with 4 vertices, no edges.
- K4, the complete graph.
- P4, path with 4 vertices.
- K1,4, complete bipartite, star graph.
- C4, cycle with 4 vertices.
- This tree:
- Compute the number |C| of colorings with colors {1,2,..,k}, up to symmetry, for the above graphs. Use direct positive counting techniques such as the Four Essential Problems, and/or Burnside's Formula. Note: These are classes of all colorings, not necessarily proper: for example, all vertices might have the same color.
- Counting graphs. There are 8 possible graphs on the vertex set V = {1,2,3}, defined by their edge sets:
E = {}, {12}, {13}, {23}, {12, 13}, {12, 23}, {13, 23}, {12, 13, 23}. In this problem, consider all possible graphs G on the vertex set V = {1,...,6}.- How many possible graphs G?
- How many possible 6-vertex paths G = P6?
- How many possible trees G = T?
- How many possible forests with two tree components, G = T ∪ T' ? Hint: Split into cases depending on the size of the components.
- How many possible cycles C6?
- Extra Credit: How many possible forests (acyclic graphs) with any number of components? More generally, find a way to count forests on n vertices.
- Extra Credit: For each graph in #1, compute |P|, the number of proper colorings up to symmetry. (See the extension of Burnside's Theorem described above.)
- Extra Credit:
Count the number of trees with n vertices in which
v1,..., vn−2 are labeled,
and the remaining two vertices remain unlabeled.
For example, for n = 3, there are two such trees:
v1−−v−−v
and v1−−v−−v;
and for n = 4 there are nine trees.
Hint: Consider the trees on n labeled vertices, under the symmetry σ which switches the labels vn−1 and vn. Use Burnside's Theorem to count the symmetry classes. Only certain special trees will be fixed under σ.
Burnside gives: |C| = 1⁄24(k4 + 6k3 + 11k2 + 6k).
Easier way: a coloring of the unordered vertices is the same as a multiset of 4 objects from k kinds, i.e. ((k | 4)) = (k+3 | 4) = (k+3)(k+2)(k+1)k / 4! .
1b & 2b. Same symmetry group Γ = S4, so the same coloring classes as in 2a.
1c & 2c. Γ = {(1)(2)(3)(4), (14)(23)}, so Burnside gives |C| = ½(k4 + k2) = ½k2(k2+1).
1d. Γ = S4 (similar to the Example above).
1e. Γ = D4, the dihedral symmetry group of the square, containing the identity, 2 rotations, 4 reflections. See HW 2/24 #2.
1f & 2f. The symmetries of Γ = Sym(G) are as follows:
- id = (1)(2)(3)(4)(5)(6) the identity mapping
- τ1 = (12)(3)(4)(56) top-to-bottom reflection
- τ2 = (15)(26)(34) side-to-side reflection
- ρ = (16)(25)(34) 180° rotation
- σ1 = (12)(3)(4)(5)(6) twist left fork, leave the rest alone
- σ2 = (1)(2)(3)(4)(56) twist right fork, leave the rest alone
- σ1τ2 = τ2σ2 = (1526)(34)
- σ2τ2 = τ2σ1 = (1625)(34)
Burnside's Theorem gives the number of coloring classes: |C| = 1⁄8 (k6 + 2k5 + k4 + 2k3 + 2k2).
3a. There are (6 | 2) = 15 possible edges between n vertices, so the largest possible edge-set, the edges of the complete graph K6, is Emax = {e1,..., e15}. The edge-set of every other graph is a subset of this: E ⊂ Emax. The number of possible subsets of a 15-element set is 215. Alternatively, think of the 15 possible edges as on or off (present or absent), a sequence of 15 independent binary choices, making 215 possibilities in all. Ans: There are 2(6 | 2) = 215 = 32768 possible graphs.
3b. A path is just an ordering of the 6 vertices, and there are 6! ways to do this (Basic Problem 1). However, this is double-counting, since paths each path is the same as its reverse path. Ans: 6! / 2 = 360.
3c. Cayley's Theorem says there are nn−2 = 64 = 1296 trees on n = 6 vertices.
3d. First, we split the vertex set {1,...,6} into two components of size k and 6−k, where k = 1,2,...,5. Then we choose from kk−2 trees in the first component and (6−k)6−k−2 trees in the second component. However, this is double-counting, since each (k, 6−k) forest is the same as one of the (6−k, k) forests. Ans:
= (6 | 1)53 + (6 | 2)2042 + ½(6 |3)3131 = 1080.
3e. We can specify a cycle as a list of vertices, of which there are 6!; however, this overcounts, and we must divide by the symmetry group of the cycle C6, namely by Γ = D6, the rotation and reflection symmetries of a regular hexagon. Answer: 6!⁄2(6) .