Final Exam Review III
Here we review some theory problems from past exams. Answer the following questions and justify using the definitions and theorems we have covered (in class notes, homework, and coursepage notes.
- Using the basic properties of choose numbers (n | k), prove that:
- (20 | 10) = (18 | 10) + 2(18 | 9) + (18 | 8).
- ((20 | 10)) = ((11 | 19))
- Consider the following graph G, which is a subdivision of K5
in which each edge has been replaced by a path with 2 edges.
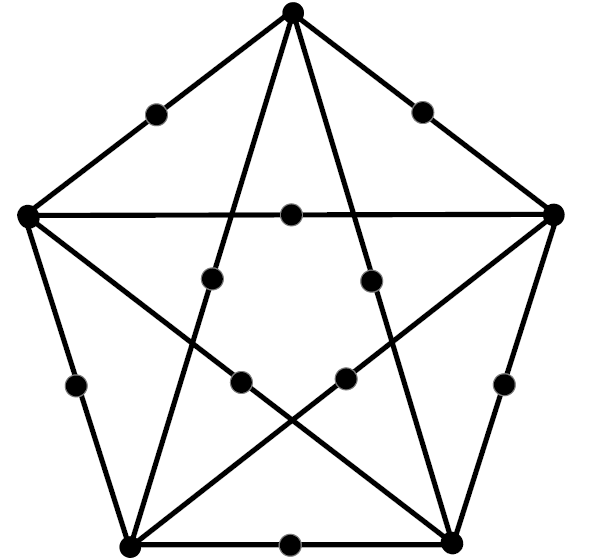
- Is G a tree?
- Is G bipartite?
- Is G planar?
- Is G a regular graph (that is, vertex-regular)?
- Determine the chromatic number χ(G).
- Let G be a forest graph consisting of two connected components which are trees, with vertex set V={1,2,..., 9}.
- How many edges does G have? Justify using results we have covered.
- How many possible such graphs are there? For example, G might consist of two paths:
2−5−3
4−7−1−6−8−9
Hint: Start by choosing the sizes of the two trees.
- Let G be a graph with all the following properties:
- G is bipartite.
- G is non-planar
- G does not contain K3,3 or any subdivision of K3,3
Problem: Draw an example of such G, and show it satisfies the three properties.
- What is the maximum possible number of regions in a drawing of a planar graph with n vertices?
- Explicitly define the tree T = (V,E) corresponding to the Prufer code of 20 consecutive 1's:
s = (1,1,...,1).
Answers
1a. Twice applying the Pascal Triangle Identity (n | k) = (n−1 | k) + (n−1 | k−1), we compute:
(20 | 10) = (19 | 10) + (19 | 9) = (18 | 10) + (18 | 9) + (18 | 9) + (18 | 8)
= (18 | 10) + 2(18 | 9) + (18 | 8).
1b. Applying the Bins-and-Beans Identity ((n | k)) = (n+k−1 | k), and the Pascal's Triangle Symmetry (n | k) = (n | n−k), we compute:
((20 | 10)) = (29 | 10) = (29 | 19) = ((11 | 19)).
2a. G is not a tree since it has cycles (whereas a tree is connected and acyclic).
2b. G is bipartite, since it is easy to mark the vertices with +/− so that all edges go between + and − (which is the same as a proper 2-coloring). In fact, mark all the degree 4 vertices (the original vertices of K5) with +, and all the degree 2 vertices (the subdivision points) with −.
2c. G is non-planar, since it contains a subdivision of K5. (Thus, if we could draw G without edge-crossings, we could erase the subdivision points, and get a planar drawing of K5 itself, which we know is impossible.)
Alternatively, we could quote Kuratowski's Theorem: a graph is non-planar if and only if it contains a subdivision of K5 or K3,3,.
2d. Since G has some vertices of degree 2 and some of degree 4, it is not a regular graph (which is when deg(v) is the same for all v).
2e. Since G is bipartite (and contains an edge), we have χ(G) = 2. In fact, χ(G) = 2 ⇔ G is bipartite with at least one edge.
3a. Suppose G splits into tree components as G = T1 ∪ T2 with n1 and n2 vertices, having n1 + n2 = 9.
Since the components are trees, their respective number of edges is n1−1 and n2−1, for a total of
|E| = n1−1 + n2−1
= n1 + n2 − 2
= 9−2 = 7.
3b. We split the possibilities into cases according to the sizes of the components (n1, n2), where we assume n1 is for the smaller component. Thus (n1, n2) = (1,8), (2,7), (3,6), or (4,5).
If these sizes are fixed, there are (9 | n1) ways to choose the vertices of T1, which also determines the vertices of T2. Then by Cayley's Theorem, the number of possible trees on the fixed n1 vertices is n1n1−2, and on the other n2 vertices it is n2n2−2 . The total of all cases is thus:
(9 | 1) 86 + (9 | 2) 2075 + (9 | 3) 3164 + (9 | 4) 4253.
4. The K5 subdivision in #2 above is such a graph. It is bipartite by #2b and non-planar by #2c. It cannot contain any subdivision of K3,3, since it has only 5 vertices with deg(v) ≥ 3, whereas any subdivision of K3,3 would have 6 vertices with deg(v) = 3.
5. Assume G is a planar graph with n vertices and a maximal number of regions. Adding extra edges to G never reduces the number of regions, so if G is not connected, we may draw enough edges to make it connected. For connected G, we may apply Euler's Formula n − q + r = 2 to get r = 2 − n + q. Here n is fixed, so the maximum r is achieved with the maximum q. But we know a maximal planar graph has q = 3n−6 edges, so the maximum r is:
r = 2 − n + q = 2 − n + (3n−6) = 2n − 4.
Alternatively, all regions of G must be triangles (since if one region were not, we could draw a diagonal edge increasing the number of regions). Thus G is maximal planar, and q = 3n−6. Also, the Region-Edge Inequality becomes the equality 3r = 2q, so that r = 2q⁄3 = 2⁄3(3n−6) = 2n−4.
6. Since the sequence has n−2 = 20 entries, the tree must have n = 22 vertices, which we may write as V = {v1, v2,..., v22}, so the Prufer sequence can be written s = (v1,..., v1). The Reverse Prufer Algorithm says to draw an edge between the first entry s1 = v1 and the smallest element of V which does not appear in s, namely e1 = v1v2. Now we cross out the first entry of s and the element v2 from V, and repeat, getting e2 = v1v3. Continuing, we eventually get e20 = v1v21, and we add one more edge between the remaining vertices, e21 = v1v22. That is, E = {e1,..., e21}, where ei = v1vi.
Alternatively, we could note that the Prufer sequence s contains every vertex of V except the leaves of T. Thus all the vertices v2,..., v22 are leaves, and T could only be the star graph K1,21 with v1 at the center.
