MTH 254H
Old Assignments

I will give 1 extra point to the first person reporting each significant typo or error on this page. Corrections and recent revisions are in red. Tentative future assignments are marked in gray.

• ⊞ Before 1/11
  Review the basic facts about the cosine function, such as its definition in terms of triangles and the shape of its graph.

• ⊞ 1/11: Lect 1. Vectors, dot product, orthogonal decompostion, area. 
  Reading: Class notes; also useful notes here and here. Start the Weekly HW due 1/15 below.
  HW: We will write a vector interchangeably as:

  • v = AB an arrow from point A to B, which could be drawn equivalently starting at any point in the plane;
  • v = (x,y), the standard form giving the endpoint if the vector is drawn starting at (0,0).

  Asterisk (*) indicates topics I did not get to in lecture: postpone the marked problems.
  Problems:

  1. Define points O = (0,0), A = (1,3), B = (3,0), C = (3,2).
     1. Determine the standard form for vectors AB and OC, and show that they are orthogonal.
     2. Write the parametrized line through A,B in the form l(t) = u + t v. (That is, l(t) is a vector from (0,0) to any point on the line.) Do the same for the line through O,C.
     3. Find the intersection point of the two lines. Hint: Write the lines as functions of different parameter variables l(t) and m(s), write the equation l(t) = m(s) in coordinates, and solve the resulting system of linear equations for variables s,t.
     4. (*) Find the area of the triangle ΔAOB. Hint: It is half the area of the parallelogram spanned by vectors OA and OB, which is a determinant.
     5. (*) Find the area of the quadrilateral □AOBC. Hint: It is not a parallelogram, so you must separately compute the areas of two triangles which compose it.
  2. Consider vectors u = (0, −10) and v = (3,2), and let p = p_uv be the orthogonal (perpendicular) projection of u on the direction v.
     
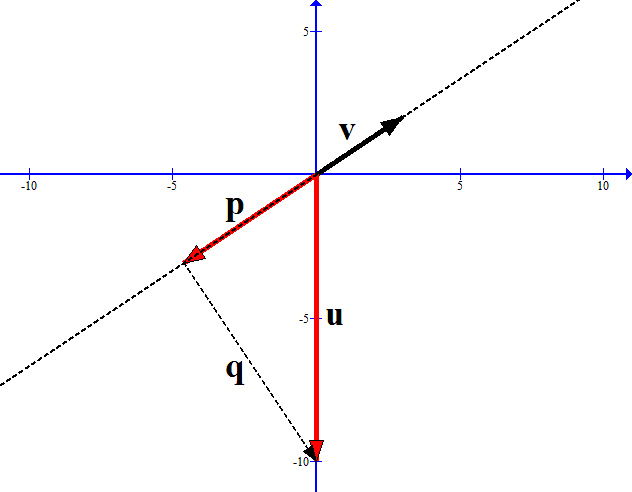
     1. Find the length |p| by computing the dot product u • v, then recalling our original definition u • v = ±|p| |v|.
     2. Determine p by finding a scalar multiple p = sv with the correct length |p| and sign.
     3. Verify that p = (^{u • v}⁄_{v • v}) v.
     4. Write the orthogonal decomposition u = p + q, where p is parallel to v, and q is orthogonal to v.
     5. If v points along an inclined plane, and u represents the acceleration for a free-falling object (about 10 m/sec²), then what is the acceleration of an object sliding without friction along the plane? What is the force of the object against the plane?
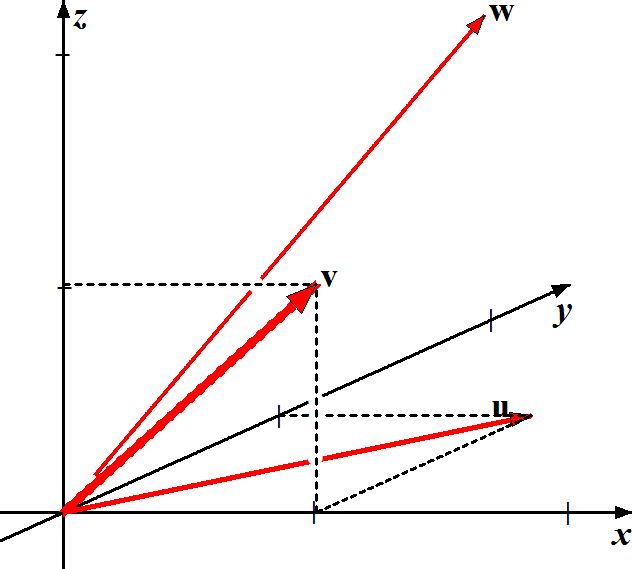
  3. Given a triangle whose vertices are (the endpoints of) u, v, w, the centroid or center of gravity is: c = ¹⁄₃(u + v + w), the point whose x-coordinates are the average of the x-coordinates of the vertices, and same for the y-coordinates.
     A median of the triangle is the line segment from a vertex to the midpoint of the opposite side.
     Using vector algebra, prove that the three medians all intersect at the centroid, which is ²⁄₃ of the way along each median.
     1. Write each median as a parametrized line segment.
     2. Show that the point ²⁄₃ of the way along each median is indeed the centroid.
  ⊞ Solutions

  1a. Vector AB = B − A = (3,0) − (1,3) = (2,−3);   OC = (3,2). The dot product is: AB • OC = (2,−3) • (3,2) = (2)(3) + (−3)(2) = 0, meaning the vectors are orthogonal.

  1b. l(t) = A + t (AB) = (1,3) + t (2,−3) = (1 + 2t, 3 − 3t) and m(s) = s (3,2) = (3s, 2s).

  1c. The lines intersect when l(t) = m(s), which means: 1 + 2t = 3s and 3 − 3t = 2s. Solving this linear system, for example by substitution, gives: (t,s) = (⁷⁄₁₃, ⁹⁄₁₃), so l(⁷⁄₁₃) = m(⁹⁄₁₃) = (²⁷⁄₁₃, ¹⁸⁄₁₃) is the intersection point.

  1d. The signed area of the parallelogram is: det(OA,OB) = det(1,3; 3,0) = (1)(0) − (3)(3) = −9. Alternative computation: OA^⊥ • OB = (−3,1) • (3,0) = −9. (The negative sign indicates a clockwise turn from OA to OB, rather than the standard counterclockwise orientation.) Thus, the (absolute) area of the triangle is ½ |−9| = ⁹⁄₂.

  1e. The area of ΔACB is ½ det(A−C ; B−C) = ½ det(−2,1; 0,−2) = ½((−2)(−2) − (0)(1)) = 2.
  Adding the areas of ΔAOB and ΔACB gives ⁹⁄₂ + 2 = ¹³⁄₂.

  2a. We compute: u • v = (0, −10) • (3,2) = (0)(3) + (−10)(2) = −20, and |v| = √(3² + 2²) = √13 . Then |p| = ^{|u • v|}⁄_|v| = ²⁰⁄_√13.

  2b. We have: ²⁰⁄_√13 = |p| = |s| |v| = s√13, so s = ^±20⁄₁₃ and p = s v  =  ^±20⁄₁₃ (3,2) = ±(⁶⁰⁄₁₃, ⁴⁰⁄₁₃). In fact, we need the − sign, p  =  ⁻²⁰⁄₁₃ (3,2), since there is an obtuse angle between u and v, so the projection p points opposite to v.

  2c. The result in (b) agrees with the general formula: p = (^{u • v}⁄_{v • v}) v = ⁻²⁰⁄₁₃ (3,2).

  2d. q = u − p = (0, −10) + ²⁰⁄₁₃ (3,2) = (⁶⁰⁄₁₃, ⁻⁹⁰⁄₁₃).
  Here q is indeed orthogonal to v, because:

  q • v  =  (u − p) • v  =  (u − (^{u • v}⁄_{v • v}) v) • v
   =  (u • v) − (^{u • v}⁄_{v • v}) (v • v)  =  0.

  2e. Here p is the component of acceleration along the plane v, so the acceleration is |p| = ²⁰⁄_√13 ≈ 5 m/sec², about half the acceleration of free-fall. The force on the surface is mass times acceleration, so it depends on how heavy the object is. A 1 kg object (pressing about 10 Newtons on a flat surface) would exert a force of 1 |q| = ³⁰⁄_√13 ≈ 8 N.

  3. See the whole solution written as a model proof.
  3a. The vector from u to the midpoint ½(v + w) is: ½(v + w) − u = ½v + ½w − u. The median line segment is:

  m(t)  =  u + t (½v + ½w − u)  =  (1−t)u + ½t v + ½t w,     for 0 ≤ t ≤ 1.

  (Here we expanded using the distributive property of scalar multiplication over vector addition.) Similarly for the other medians.

  3b. m(²⁄3) = ¹⁄3 u + ¹⁄3 v + ¹⁄3 w = c. Doing a similar computation for the other medians, we see that the same point c lies on all three lines.

• ⊞ 1/13: Lect 2. Scalar-valued function f : R² → R, graph & contour plot; linear approximation and partial derivatives; vector fields, gradient. 
  Reading: Class notes, M&T Ch 2.1. Don't forget the Weekly HW due 1/15 below.
  HW:

  1. Consider the function ℓ : R² → R given by ℓ(x,y) = x + 3y.
     1. Find the vector m such that ℓ(v) = m • v, where • is dot product of vectors.
     2. Draw the contour map of ℓ, namely the lines on which ℓ is a given constant, defined by equations x + 3y = c for c = ..., -1, 0, 1,....
     3. Find the uphill direction perpendicular to the contour lines. Explain why it is the same as m.
     4. Compute the partial derivatives ^∂ℓ⁄_∂x, ^∂ℓ⁄_∂y, and write the gradient vector field ∇ℓ(x,y) = (^∂ℓ⁄_∂x, ^∂ℓ⁄_∂y). Explain why this is a constant vector field equal to m. Draw the gradient vector field onto the contour map. (Since ∇ℓ is constant, this means drawing the same vector at each grid point.)
     5. Do your best to draw the graph z = ℓ(x,y).
  2. Consider the function f : R² → R given by f(x,y) = x² + y.
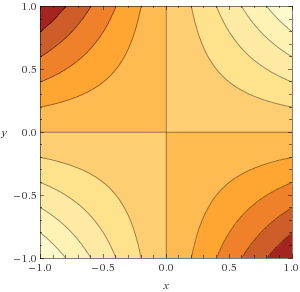
     1. Draw the contour map of f, that is the parabola curves where f is constant, defined by x² + y = c for c = ..., -1, 0, 1, ....
     2. Compute the partial derivatives ^∂f⁄_∂x, ^∂f⁄_∂y, and write the gradient ∇f(x,y) = (^∂f⁄_∂x, ^∂f⁄_∂y).
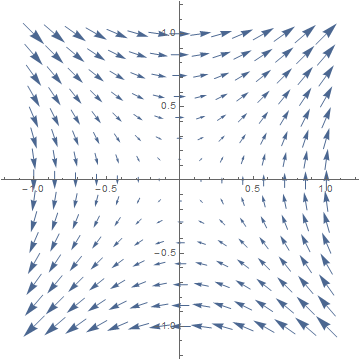
     3. Draw the gradient vector field onto the contour map, namely at each grid point (x,y), draw the arrow ∇f(x,y) starting at (x,y).
     4. Near the point (1,1), draw the line defined by ∇f(1,1) • (x,y) = ∇f(1,1) • (1,1). Explain why this is tangent to the contour which passes through (1,1), namely f(x,y) = f(1,1) = 2.
     5. Draw the graph z = f(x,y), which looks like a tilted trough. The easiest way is to draw its "ribs", the vertical parabolas z = x² + c above the horizontal lines y = c. On the same drawing, draw the horizontal slices defining the contour lines f(x,y) = c.
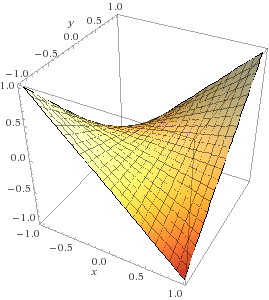
  3. Draw the contour map, gradient vector field, and graph for the function f(x,y) = xy. The graph is called a saddle surface.
  4. For the function f(x,y) = x³ − 3x − y², have a computer draw its graph, contour plot and gradient vector field. Locate the critical points, where the gradient vanishes, by solving ∇f(x,y) = (0,0), and verify the answers visually on your gradient plot. Visually classify each critical point as:
     • a local maximum, where the gradient arrows all point in
     • local minimum, where the arrows point out
     • saddle point, where one direction points in, another out.
     Inspect these critical points on the graph and the countour plot.
  5. Consider a rectangular bin having a bottom but no top, and three sides with the fourth side open. Assuming it has volume 1, find the length, width and height which will minimize the total surface area of the three sides and bottom.
     Hint: Write the surface area as s(x,y), a function of the length x and width y (with the height z determined by volume = 1). Then the unique critical point, where ∇s(x,y) = (0,0), is the minimum point of s(x,y).
  ⊞ Solutions

  1a. Clearly m = (1,3) has ℓ(v) = m • v = (1,3) • (x,y) = x + 3y.

  1b,d. Contour lines ℓ(x,y) = c, with gradient vector field ∇ℓ(x,y) = (1,3), not to scale:

  
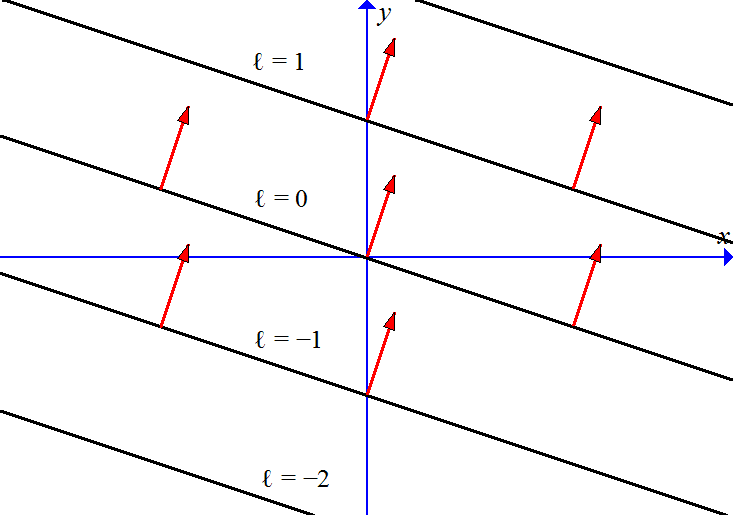
  1c. The uphill direction at every point is m = ∇ℓ(x,y) = (1,3). One way to see this: the contour through the origin is defined by m • (x,y) = 0, which means that any vector (x,y) in this contour is orthogonal to m. More generally, if two vectors (x,y) = v or v' both lie on the same contour m • (x,y) = c, then the vector between them, v − v', satisfies

  m • (v − v') = m • v − m • v' = c − c = 0.

  That is, the direction v − v' along the contour is orthogonal to the gradient vector m.

  2a,b,c. Below are contour curves f(x,y) = c; the gradient vector field ∇f(x,y) = (2x, 1), not to scale; also the tangent line from part (d).

  
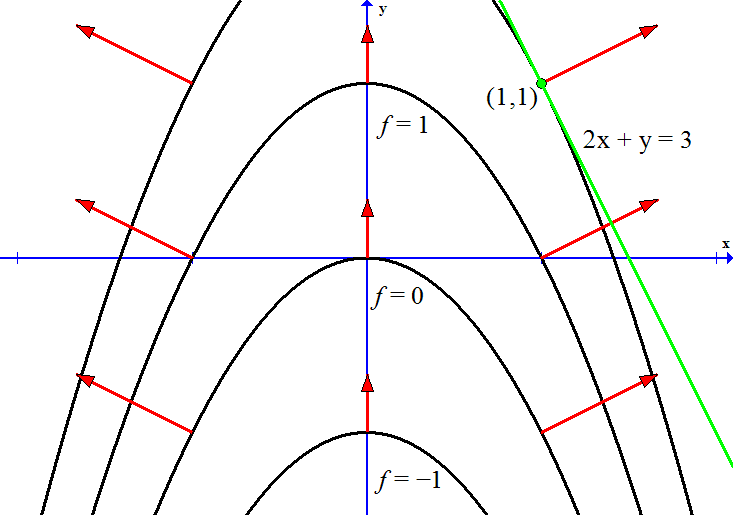
  Notice that away from the y-axis, there is a steeper uphill slope, which is indicated by closer contour lines, and by longer gradient vectors. Also, if you zoom in on any small part of this non-linear picture, it looks approximately like the linear picture in Prob 1.

  2d. The contour curve of f(x,y) passing through (1,1) is given by the equation f(x,y) = f(1,1) = 2. If we zoom in near (1,1), the contour curve looks approximately linear, indistinguishable from its tangent line. To put this in equations, consider the affine approximation:

  f(x,y)  ≈  ℓ(x−1, y−1) + f(1,1)  =  ∇f(1,1) • (x−1, y−1) + f(1,1)  =  2x + y − 1.
  The tangent line is the contour of ℓ(x,y), given by the equivalent equations:

  ℓ(x−1, y−1) + f(1,1) = f(1,1)   ⇔   ∇f(1,1) • (x,y) − ∇f(1,1) • (1,1) = 0   ⇔   ∇f(1,1) • (x,y) = ∇f(1,1) • (1,1).

  2e. With vertical ribs, and with horizontal contour lines:

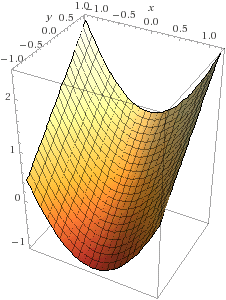
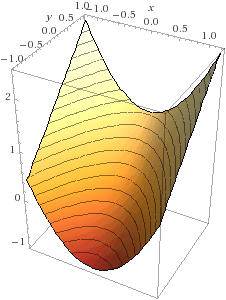
  I got these images from Wolfram Alpha, which is a great resource for computations and pictures.

  3. The contour plot consists of the axes (xy = 0), and hyperbolas y = c/x. The gradient is ∇f(x,y) = (y,x): we have ^∂⁄_∂x(xy) = y, since in the partial derivative with respect to x, the variable y is considered as a constant. In the graph z = xy, the vertical curve above y = x is the upward parabola z = x², while above y = −x it is the downward parabola z = −x², making a "saddle".

  
  4. f(x,y) = x³ − 3x − y² has gradient ∇f(x,y) = (3x² − 3, −2y):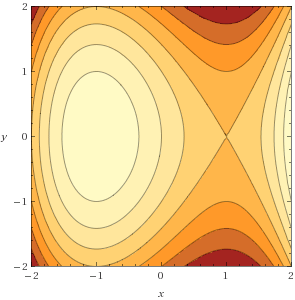

  
  The critical points are given by (3x² − 3, −2y) = (0,0), namely (x,y) = (±1,0). Then (−1,0) is a local maximum (hilltop) of the graph z = f(x,y), since the nearby gradient vectors (the uphill vectors) all point inward toward the point. This looks like a bullseye on the countour plot.
  Also (1, 0) is a saddle point, since along the horizontal axis, the nearby gradient vectors point outward from the point, but along the vertical axis, they point inward to the point. This looks like a crossroad on the contour plot.

  5. Letting x,y,z be the side-lengths of the rectangular bin, the volume is xyz = 1, and the surface area of the four sides is s = xy + yz + 2xz. Eliminating the variable z = ¹⁄_xy, we get the function

  s(x,y) = xy + ¹⁄_x + ²⁄_y   for   x,y > 0.

  The gradient field is: ∇s(x,y) = (y − ¹⁄_x² , x − ²⁄_y²):

  

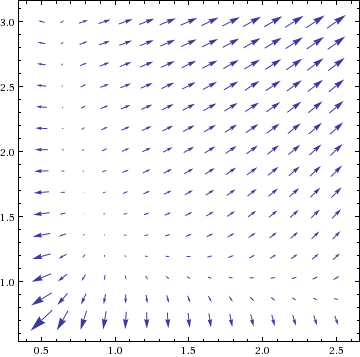
  The only critical point, where ∇s(x,y) = (y − ¹⁄_x², x − ²⁄_y²) = (0,0), is (x,y) = (2^−1/3, 2^2/3) ≈ (0.8, 1.6). The vector field plot shows this is a local minimum, since the uphill vectors all point outward from this point. For completeness, we should also consider the critical points where ∇s is undefined, namely the boundary points where x = 0 or y = 0; but these are clearly vertical asymptotes where s(x,y) tends to infinity.
  Thus, our final answer is: (x,y,z) = (2^−1/3, 2^2/3, 2^−1/3).

• ⊞ 1/15: Lect 3. Fundamental Theorem of Calculus, line integrals, Gradient Theorem, parametrized curves 
  Reading: Class notes, Summary notes. Weekly HW was due in class today.
  HW:

  1. Consider the vector field: F(x,y) = (2x, 1).
     1. Find the line integral ∮ F(c) • dc along the path c(t) = (3t, 5t), from c(0) = (0,0) to c(1) = (3,5). Now, assuming the vector field is the gradient of a scalar function, F = ∇f, with f(0,0) = 0, find f(3,5).
     2. Find the line integral ∮ F(c) • dc along the path c(t) = (at, bt), from c(0) = (0,0) to a general point c(1) = (a,b). Find the potential function f(a,b) and verify that ∇f = F.
     3. Do part (c) using a different path c(t). Namely take c(t) = (at, 0) for 0 ≤ t ≤ 1, and c(t) = (a, b(t−1)) for 1 ≤ t ≤ 2. This goes from c(0) = (0,0) to c(1) = (a,0) to c(2) = (a,b). Then compute:
        ∮ F(c) • dc   =   ∫₀² F(c(t)) • c'(t) dt.

        Hint: Split the integral into intervals, ∫₀² = ∫₀¹ + ∫₁².

  2. Consider the vector field: F(x,y) = (x,y)^⊥ = (−y, x).
     1. Sketch the vector field F, which looks like a spinning vortex, getting stronger farther from the center. This is the velocity field of a turn-table: the speed of each point is proportional to its distance from the center of rotation.
     2. Could F have a potential function f, whose gradient field is F? That is, could F be pointing in the uphill direction of a graph z = f(x,y)?
     3. Try to use the Gradient Theorem to find a potential function f with F = ∇f, as in Prob 1(b) above. That is, compute f(a,b) = ∫_c F(c) • dc for the straight-line path c(t) = (at, bt). Does this give a correct potential function f?
     4. Next, try the line integral along the second path c in Prob 1(c). Does this give a correct potential function?
  3. We consider line integrals of the vector field:
     F(x,y) = (e^y, xe^y).
     1. Let c(t) = (at, bt) for 0 ≤ t ≤ 1, and determine f(a,b) = ∮ F(c) • dc. Verify that ∇f = F.
     2. Now consider the curve p(t) = (x(t), y(t)) = (t, t²) from p(0) = (0,0) to p(1) = (1,1). Explain why we cannot evaluate ∮ F(p) • dp = ∫¹₀ F(p) • p'(t) dt as we usuallly do, by finding an antiderivative.
     3. Determine the line integral ∮ F(p) • dp from part (b), by considering that F = ∇f from part (a), and applying the Gradient Theorem.
     4. Approximate the line integral in (b) directly from the definition: ∮ F(p) • dp  =  ∑ _i=1 ⁿ F(p_i) • Δp_i.
        Specifically, make a computer spreadsheet for n = 10, with rows corresponding to i = 0, 1,..., 10, and columns which calculate:
        1. t_i = ⁱ⁄_n
        2. x_i = t_i
        3. y_i = t_i²
        4. F₁(p_i) = exp(y_i)
        5. F₂(p_i) = x_i exp(y_i)
        6. Δx_i = x_i − x_i−1
        7. Δy_i = y_i − y_i−1
        8. F(p_i) • Δp_i  =  F₁(p_i)Δx_i + F₂(p_i)Δy_i
        (The last three columns will have no entry for i = 0.) Finally, sum up the last column (something like =SUM(H4:H13)) to get an approximation for ∮ F(p) • dp. Compare to your exact answer from part (c).
        Hint: You only need to enter the formulas in the top couple of rows, then fill down.
     5. In part (d), we used the right-endpoint samples F(p_i) in the Riemann sum for the line integral. Improve the approximation by taking the midpoint samples F(p_i^~), where p_i^~ = ½(p_i + p_i−1). How much accuracy did this gain?
        Note: Here we compute approximations even though we know the exact value; but for a general line integal, it is often impossible to find an exact value, and approximation is all we can do.
  ⊞ Solutions

  1a.   f(3,5)   =   ∮ F(c) • dc   =   ∫₀¹ F(c(t)) • c'(t) dt   =   ∫₀¹ F(3t,5t) • (3t, 5t)' dt
    =   ∫₀¹ (6t,1) • (3,5) dt   =   ∫₀¹ 18t + 5 dt   =   9t² + 5t |¹_t=0   =   14.

  1b. We repeat part (a) with (3,5) replaced by (a,b), getting f(a,b)   =   ∮ F(c) • dc   =   ∫₀¹ (2at,1) • (a,b) dt   =   ∫₀¹ 2a²t + b dt   =   a² + b. Thus, f(x,y) = x² + y, and ∇f(x,y)   =   (^∂⁄_∂x(x² + y), ^∂⁄_∂y(x² + y))   =   (2x, 1).

  1c.

  f(a,b)   =   ∮ F(c) • dc
    =   ∫₀¹ F(at, 0) • (at, 0)' dt  +  ∫₁² F(a, b(t−1)) • (a, b(t−1))' dt
    =   ∫₀¹ (2at, 1) • (a, 0) dt  +  ∫₁² (2a, 1) • (0, b) dt
    =   ∫₀¹ 2a²t dt  +  ∫₁² b dt   =   a² + b.

  Thus, f(x,y) = x² + y agrees with in part (b), which is guaranteed by the Gradient Theorem.

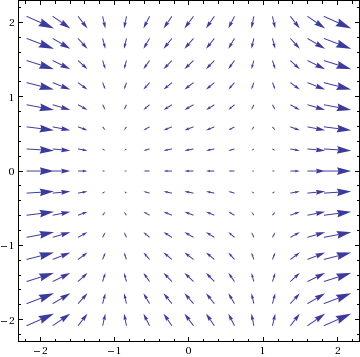
  2a. The vortex vector field F(x,y) = (−y, x):

  

  2b. From the vector field plot, we can see that F could not have any potential function f. If F(x,y) were the gradient or uphill direction for a graph z = f(x,y), we could follow an uphill path all the way around a circle centered at the origin, which is obviously impossible.

  2c. f(a,b)   =   ∫₀¹ (−bt, at) • (a,b) dt   =   ∫₀¹ −bat + abt dt   =   0.
  That is, the vector field is everywhere orthogonal to the curve, and f(x,y) = 0 is the zero constant function. The gradient is ∇f(x,y) = (0,0) ≠ F(x,y), so the method fails, which means F(x,y) could not have been a gradient in the first place.

  2d.   f(a,b)   =   ∫₀¹ F(at, 0) • (at, 0)' dt + ∫₁² F(a, b(t−1)) • (a, b(t−1))' dt   =   ∫₀¹ (0,at) • (a, 0) dt + ∫₁² (−b(t−1), a) • (0, b) dt   =   ab.
  Thus f(x,y) = xy, but this also fails to give a potential function, since ∇f(x,y) = (y,x) ≠ F(x,y). If one path fails to give a correct potential function, no other path will work.

  3a. f(a,b) = ∮ F(c) • dc = ∫¹₀ F(c(t)) • c'(t) dt = ∫¹₀ F(at, bt) • (at, bt)' dt = ∫¹₀ (e^bt, at e^bt) • (a, b) dt = ∫¹₀ a e^bt + abt e^bt dt = at e^bt |¹_t=0 = a e^b.
  Therefore f(x,y) = x e^y.

  3b. We try: ∮ F(p) • dp = ∫¹₀ F(t, t²) • (t, t²)' dt = ∫¹₀ e^t2 + 2t²e^t2 dt.
  But ∫ e^t2 is well known to have no algebraic anti-derivative, and it is easy to deduce that the above integral also has none. Thus, our algebraic methods are stuck.

  3c. By the Gradient Theorem, ∮ F(p) • dp = f(p(1)) − f(p(0)) = 1e¹ − 0e⁰ = e = 2.718...

  3d. Spreadsheet. We get ∮ F(p) • dp ≈ 3.0, which is about 10% over the exact value e = 2.718... from part (c). This is expected, since F(p(t)) is increasing in magnitude, so its average value within each interval is less than at the right endpoint F(p_i).

  3e. Spreadsheet. This time, the approximation ∮ F (p) • dp ≈ 2.714 is accurate to 2 decimal places, which is pretty impressive since Δt = 0.1 has only one decimal place.

• ⊞ 1/20: Lect 4. Potential functions and path independence, curl, double integrals. 
  Reading: Class notes, Notes 1/20−22 on Double Integrals, Curl. See the Weekly HW due 1/22 below.
  In this HW, you compute with two concepts which I will explain in the next lecture.

  • For a vector field F, its curl is a scalar function which measures the "rate of rotation" of F near a given point (x,y). If we think of F as the velocity field of a fluid, curl F(x,y) is the turning force felt by a small paddlewheel placed in the flow at (x,y). (Couterclockwise turn means positive curl, clockwise means negative.) For F(x,y) = (p(x,y), q(x,y)), its curl is computed as the difference of certain partial derivatives of the components:
    curl F(x,y)  =  ^∂q⁄_∂x − ^∂p⁄_∂y .

    In fact, F has a potential function with F = ∇f if and only if curl F = 0 everywhere.

  • The double integral ∬_R f(x,y) dy dx measures the volume under the graph z = f(x,y) and above the region R in the xy-plane. It is computed by doing the inside integral ∫ f(x,y) dy with respect to the variable y, considering x as a constant; the result is a function of x, which we then integrate with respect to x.
    Example: For the rectangular region R with 0 ≤ x ≤ 1 and 2 ≤ y ≤ 3, we have: ∬_R xy² dy dx = ∫¹₀ ∫³₂ xy² dy dx = ∫¹₀ ⅓ xy³ |³_y=2 dy = ∫¹₀ ⅓(27x − 8x) dx = ¹⁹⁄₆.

  
  HW:

  1. For each of the following vector fields F:
     • Sketch F, and visually estimate curl F, the rate of rotation at each point: this is how strongly a little paddlewheel would be turned around the point (x,y) in the flow given by F.
     • For F(x,y) = (p(x,y), q(x,y)), compute curl F = ^∂q⁄_∂x − ^∂p⁄_∂y, and compare to your estimate.
     • If curl F = 0 everywhere, find the potential function f = ∮ F(c) • dc with ∇f = F.
     The fields are:
     1. F(x,y) = (0, x)
     2. F(x,y) = (x, 0)
     3. The vortex field F(x,y) = (−y, x). Imagine sitting on a turntable, with your velocity given by F. To keep from getting dizzy, you turn your head toward a fixed point on the horizon. The curl is your head's rate of rotation.
     4. Any radial field of the form F(x,y) = g(r) (x,y), where g(r) is any scalar function of the radius r = √(x² + y²). For example g(r) = ¹⁄_r² gives radial vectors of length inversely proportional to the distance from the center:
        F(x,y)  =  ¹⁄_(x²+y²) (x,y)  =  (^x⁄_(x²+y²) , ^y⁄_(x²+y²))

  2. Consider the vector field of rotation vectors inversely proportional to the distance from the center:
     F(x,y)  =  ¹⁄_(x²+y²) (−y, x)  =  (^−y⁄_(x²+y²) , ^x⁄_(x²+y²)).
     1. Verify that the length |F(x,y)| = 1/r. Sketch the vector field F, noting that it is undefined at the origin, and guess curl F.
     2. Show that curl F = 0 everywhere except at the origin. This means the rotation is all "concentrated in the center".
     3. Compute a potential function f(x,y) defined away from the negative x-axis, i.e. for any (x,y) with y ≠ 0 or x > 0. Staying away from the singular point (0,0), take a line integral along the radial line segment from (1,0) to (r,0), then a circlar arc (r cos(t), r sin(t)) from (0,r) to (a,b), where r = √(a² + b²) and t goes from 0 to arctan(b/a). The graph z = f(x,y) is a "spiral staircase" whose height equals the angle of (x,y) from the positive x-axis.
  3. Consider the triangular region R bounded by the x and y axes and by the line x + y = 1. Suppose this is a plate whose density is given by f(x,y) = x², and its weight by a double integral.
     1. Write the region as the points between two graphs y = g(x) and y = h(x), over a certain x-interval:
        R = { (x,y) with a ≤ x ≤ b and g(x) ≤ y ≤ h(x) }.

     2. Compute the double integral in the form:
        ∬_R f(x,y) dA   =   ∫^b _a ∫ ^h(x) _g(x) f(x,y) dy dx.

        First compute the inner integral ∫ ^h(x) _g(x) f(x,y) dy with respect to the variable y, treating x as a constant. The result is a function of x which you integrate in the outer integral ∫^b _a   dx.

  ⊞ Solutions

  1a. F(x,y) = (0, x)

  

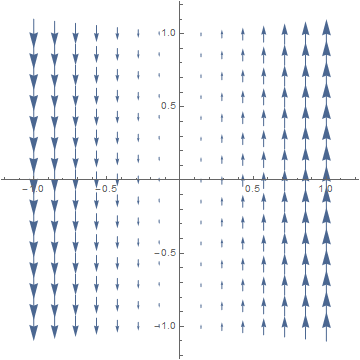
  A small paddlewheel placed at any point is pushed vertically on one side more than on the other, giving a counterclockwise rotational force, which means curl F > 0.
  In fact, curl F = ^∂⁄_∂x(x) − ^∂⁄_∂y(0) = 1 − 0 = 1. Since the curl is non-zero, the field is not path independent or irrotational, so it cannot have a potential function f.

  1b. F(x,y) = (x, 0).

  

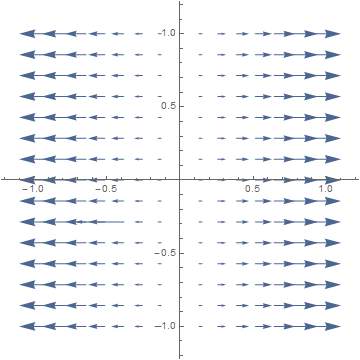
  The equal flows on the top and bottom of a paddlewheel cancel each other, so we should have curl F = 0.
  In fact, curl F = ^∂⁄_∂x(0) − ^∂⁄_∂y(x) = 0 − 0 = 0. The line integral along c(t) = (at, bt) is: f(a,b) = ∫₀¹ F(at, bt) • (at, bt)' dt = ∫₀¹ (at, 0) • (a, b) dt = ½a². The potential function is thus f(x,y) = ½x².

  1c. F(x,y) = (−y, x).

  

  A paddlewheel is pushed harder on the side away from the origin than on the side facing the origin, giving a counterclockwise rotation, curl F > 0.
  Using the other physical model, a person sitting anywhere on a turntable must turn his head at a constant rate to counter the table's rotation, so we expect curl F is constant.
  In fact, curl F = ^∂⁄_∂x(x) − ^∂⁄_∂y(−y) = 1 − (−1) = 2. There is no potential function.

  1d. F(x,y) = ¹⁄_r² (x,y).

  

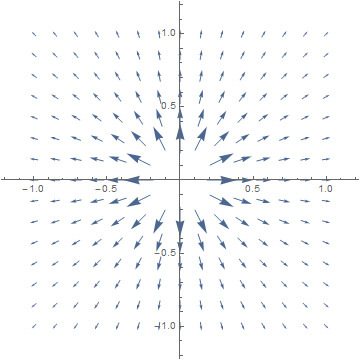
  A paddlewheel is pushed with equal force on both sides of a radial line, so we should have curl F = 0. This holds for any radial field F(x,y) = g(r) (x,y).
  We compute: r = √(x²+y²),   ^∂r⁄_∂x = ^x⁄_√(x²+y²), and similarly for ^∂r⁄_∂y, so the Chain Rule gives:

  curl F   =   ^∂⁄_∂x [g(r) y] − ^∂⁄_∂y [g(r) x]
    =   g'(r)  ^x⁄_√(x²+y²)  y   −   g'(r)  ^y⁄_{√(x² +y²)}  x   =   0.

  The potential function is f(x,y) = r G(r), where G(c) = ∫^c₀ g(r) dr.

  2a. The magnitude of F(x,y) = ¹⁄_r² (−y, x) is |F(x,y)| = ¹⁄_r² |(−y, x)| = ¹⁄_r² r = ¹⁄_r .

  

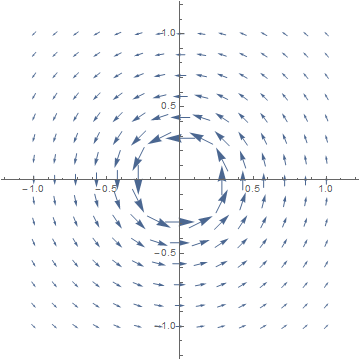
  On the side away from the center, a paddlewheel is pushed counterclockwise by the flow; on the side facing the center, it is pushed clockwise along a shorter arc by a stronger flow. The two forces balance, and we should have curl F = 0.

  2b. For F(x,y) = (−^y⁄_x²+y² , ^x⁄_x²+y²), we use the Quotient Rule to get:

  curl F   =   ^∂⁄_∂x(^x⁄_x²+y²)  −  ^∂⁄_∂y(−^y⁄_x²+y²)
    =   ^{(x2 + y2 − x(2x))}⁄_(x²+y²)²  −  ^{(x2 + y2 − y(2y))}⁄_(x²+y²)²   =   0

  That is, F has no rotation at any point where it is defined, though it has some singular behavior at the origin.

  2c. To compute the potential function f(a,b), we take the line integral along a two-segment path: we define the constant s = √(a²+b²), and take the line segment c₁(t) = (t + (1−t)s, 0) from (1,0) to (r,0); then the circular arc c₂(t) = (s cos(t), s sin(t)) from (r,0) to (a,b), where t goes from 0 to θ = arctan(b/a), which is the angle from the x-axis to the radial vector (a,b). The potential function is given by:

  f(a,b)   =   ∮ F(c₁) dc₁ + ∮ F(c₂) dc₂
    =   ∫₀¹ F(st, 0) • (st,0)' dt   +   ∫₀^θ F(s cos(t), s sin(t)) • (s cos(t), s sin(t))' dt
    =   ∫₀^{1 1}⁄_r²(0, st) • (s,0) dt   +   ∫₀^{θ 1}⁄_s²(−s sin(t), s cos(t)) • (−s sin(t), s cos(t)) dt
    =   0   +   ∫₀^{θ s2}⁄_s² (sin²(t) + cos²(t)) dt   =   θ   =   arctan(b/a).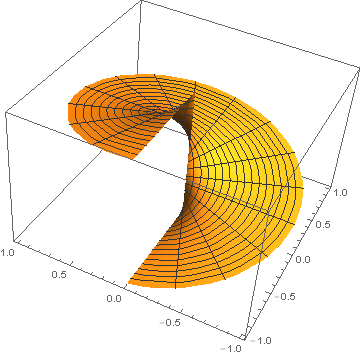

  

  In the graph z = f(x,y), the ray at angle θ from the x-axis is at height θ, for −π ≤ θ ≤ π. This leads to a discontinuity on the negative x-axis, where the angle can be either π or −π. Thus, we cannot define the potential function all the way around the origin, which reflects the fact that F does have a rotation around that point, though nowhere else.

  3a. R is the region above the interval [0,1] on the x-axis, and below the line y = 1−x, so R = { (x,y) with 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1−x }.

  3b. First, a rough estimate: the plate has area ½, but its density increases slowly from 0 on the left edge to 1 at the right corner. Thus, its weight should be much less than ½.
  Now,   ∫₀^1−x x² dy = x² y|_y=0^y=1−x = x²(1−x).
  Thus, the weight is:

  ∬_R f(x,y) dA   =   ∫₀¹ ∫₀^1−x x² dy dx   =   ∫₀¹ x²(1−x) dx   =   ¹⁄₁₂ .

• ⊞ 1/22: Lect 5. Green-Stokes Theorem (Curl Theorem)  
  Reading: Notes 1/20−22.
  HW:

  1. Consider the region R bounded by the x and y axes and the line x + 2y = 2, and the vector field F(x,y) = (0,x²). Verify the Green-Stokes Theorem for the double integral ∬_R curl F dA.
     1. State the Theorem, both in words and integral formulas.
     2. Make a sketch of the vector field and the curve, and visually estimate the total rotation around the curve, and (independently) the total curl inside the region: the Theorem says these should be the same.
     3. Compute the double integral of the rate of rotation over the region in the form ∬_R curl F dy dx: that is, set up the inside integral with respect to variable y, then the outside with respect to x.
        Hint: Write the region in the form R = {(x,y) s.t. a ≤ x ≤ b and g(x) ≤ y ≤ h(x)}.
     4. Repeat part (c) in the form ∬_R curl F dx dy, reversing the order of the dx and dy integration. You should get the same answer as before.
        Hint: Write the region in the form R = {(x,y) s.t. a ≤ y ≤ b and g(y) ≤ x ≤ h(y)}.
     5. Compute the total rotation of F around the (counterclockwise) boundary of R. You should split this into three integrals corresponding to the sides of the triangle. The Theorem says this should come out the same as part (c) and (d).
  2. In the next lecture, we will explain a new kind of derivative of a vector field F(x,y) = (p(x,y), q(x,y)), the divergence or outflow rate, a scalar function computed as:
     div F(x,y)  =  ^∂p⁄_∂x + ^∂q⁄_∂y .

     Geometrically, if F represents a fluid flow, the divergence measures the rate of net outflow (= outflow minus inflow) from a small region near (x,y), per area enclosed.
     Problem: For each vector field below, estimate from its picture whether it has positive, negative, or zero divergence at each point: does the flow going into one side of a small region balance the flow out the opposite side (div = 0, called incompressible flow), or is the fluid density thinning out at that point, so that there is faster flow out than in (div > 0)? Confirm your estimate by computing div F with the above formula. The fields are:

     1. F(x,y) = (0, x)
     2. F(x,y) = (x, 0)
     3. F(x,y) = (−y, x).
     4. A rotational field of the form F(x,y) = g(r) (−y, x), for any scalar function g(r) of the radius r = √(x² + y²).
     5. A radial field of the form F(x,y) = g(r) (x,y), for any g(r).

  ⊞ Solutions

  1a. Curl Theorem: The double integral of the rate of rotation of the vector field F over the region R is equal to the total rotation line integral of F around the boundary curve c of R:

  ∬_R curl F dA   =   ∮ F(c) • dc.

  Stating it another way: The total rotation of F around a closed curve is equal to the double integral of the rate of rotation inside the curve. (The curve must go counterclockwise to give the correct sign.)

  1b. F(x,y) = (0, x²):

  
  

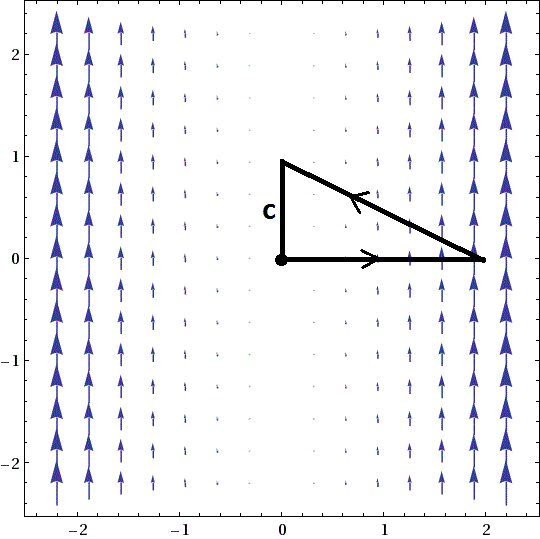
  The line integral has non-zero dot product of the field with the tangent vector only on the diagonal of the triangle, with a value about ¹⁄₂ at the middle and a maximum of about 1 at the right end. Thus, we may guess a total rotation about 1.
  For positive x, a paddlewheel would be pushed more strongly counterclockwise by the flow to its right than clockwise by the weaker flow to its left. Thus, curl F is clearly positive, and increases from zero for x = 0 to largish at x = 2; the right half of triangle has area ¹⁄₂ so the above guess of 1 is reasonable for the double integral of curl F over the triangle.

  1c. curl F(x,y) = 2x, and R = {(x,y) s.t. 0 ≤ x ≤ 2 , 0 ≤ y ≤ 1−½x}. The double integral is:

  ∬_R curl F dy dx   =   ∫₀² ∫₀^1−½x 2x dy dx   =   ∫₀² 2xy |_y=0^1−½x dx   =   ∫₀² 2x(1−½x) dx  =  ⁴⁄₃ ,

  in line with our guess.

  1d. We have R = {(x,y) s.t. 0 ≤ y ≤ 1 , 0 ≤ x ≤ 2−2y}, and:

  ∬_R curl F dx dy   =   ∫₀¹ ∫₀^2−2y 2x dx dy   =   ∫₀¹ x² |_x=0^2−2y dy   =   ∫₀¹ (2−2y)² dy  =  ⁴⁄₃ .

  Any double integral can be done either way (dy dx or dx dy), whichever is more convenient.

  1e. The boundary c has three segments: c₁(t) = (2t,0) ; c₂(t) = (2,0) + [(0,1)−(2,0)]t = (2−2t, t) ; c₃(t) = (0, 1−t), where all the parameter ranges are 0 ≤ t ≤ 1. The total rotation is:

  ∮ F(c) dc   =   ∮ F(c₁) dc₁ + ∮ F(c₂) dc₂ + ∮ F(c₃) dc₃
    =   ∫₀¹ F(2t,0) • (2,0) dt  +  ∫₀¹ F(2−2t, t) • (−2, 1) dt  +  ∫₀¹ F(0, 1−t) • (0, −1) dt
    =   ∫₀¹ 0 dt  +  ∫₀¹ (2−2t)² dt  +  ∫₀¹ 0 dt   =   ⁴⁄₃ .

  Behold the Curl Theorem!

  2a. F(x,y) = (0, x)

  

  Visually, we see that a small rectangular region has the same flow at the bottom and at the top, so net outflow is zero, the flow is incompressible, and div F = 0. Computing: div F = ^∂⁄_∂x(0) + ^∂⁄_∂y(x) = 0 .

  2b. F(x,y) = (x, 0).

  

  For a small rectangle on the right side, the inflow through its left boundary is smaller than the outflow through its right boundary, so the net outflow is positive: div F > 0. Computing: div F = ^∂⁄_∂x(x) + ^∂⁄_∂y(0) = 1.

  2c. F(x,y) = (−y, x)

  

  Consider a small curved box, a "polar coordinates box", having two sides which are short sectors of concentric circles, and the other two sides short segments of radii. Then clearly the inflow across one of the radius edges equals outflow across the other, and there is no flow across the circular edges. Thus, the net outflow is zero, incompressible flow: div F = 0. Computing: div F = ^∂⁄_∂x(−y) + ^∂⁄_∂y(x) = 0.

  2d. The same resoning as in 2(c) shows that for F(x,y) = g(r) (−y, x), we have div F = 0 for any g(r). We compute div F = 0 by applying the Chain Rule as in 2(e) below.

  2e. Let F(x,y) = g(r) (x,y) be any radial field. As in the previous part, consider a polar coordinate box: we must balance inflow of g(r) along a short curve facing the origin, with outflow of g(r+Δr) along a longer curve facing away from the origin. This can be positive, zero, or negative net outflow, depending on how quickly g(r) increases with r. Here is F(x,y) = ¹⁄_r² (x,y):

  

  We compute: r = √(x²+y²),   ^∂r⁄_∂x = ^x⁄_√(x²+y²), and similarly for ^∂r⁄_∂y, so the Chain Rule gives:

  div F   =   ^∂⁄_∂x [g(r) x] + ^∂⁄_∂y [g(r) y]
    =   g'(r)  ^x⁄_√(x²+y²)  x + g(r)   +   g'(r)  ^y⁄_{√(x² +y²)}  y + g(r)
    =   r g'(r) + 2g(r),

  which can be positive, zero, or negative. It is zero precisely when g(r) satisfies the differential equation r ^∂g⁄_∂r  +  2g = 0, which has solution g(r) = ^k⁄_r².
  Thus, the above picture is essentially the only incompressible radial field (div = 0). Of course, there is singular behavior at the origin where the field becomes infinite.

• ⊞ 1/25: Lect 6. Flux line integral, divergence, Green-Gauss Theorem  
  Reading: Notes 1/25. See the Weekly HW due 1/29 below.
  HW:

  1. Re-do HW 1/22 #2, determining divergence for several vector fields.
  2. Consider the radial field F(x,y) = ¹⁄_r² (x,y) = (^x⁄_(x²+y²) , ^y⁄_(x²+y²)), i.e. F(v) = ^v⁄_|v|² .
     This is the velocity field of water flowing from a central source and spreading out over a flat surface, like the fountain in Detroit Metro Airport.
     1. Show |F(v)| = ¹⁄_|v| = ¹⁄_r .
     2. Show that F is irrotational (zero curl) and incompressible (zero divergence).
     3. Consider the curve b(t) which is the boundary of the "polar box" defined in polar coordinates (r, θ) by ½ ≤ r ≤ 1 and 0 ≤ θ ≤ ^π⁄₄. Find the flux of F across b by visual estimation. Calculate it directly from the definition. Finally, find it using the Divergence Theorem.
     4. Now find the flux of F across the unit circle x² + y² = 1. You must first parametrize it as c(t) = (x(t), y(t)): what is the standard way to do this?
     5. The above flux of F is non-zero. How to reconcile this with the Divergence Theorem, which implies that an incompressible field (div = 0) should have zero flux across any curve? Explain!
  ⊞ Solutions

  1. See solutions to HW 1/22 #2.

  2a. |F(v)|  =  | ^v⁄_|v|² |  =  ^|v|⁄_|v|²  =  ¹⁄_|v|  =  ¹⁄_r .

  2b. We showed in HW 1/20 #1(d) that any radial field F(v) = g(r) v is irrotational. We showed in HW 1/22 #2(e) that our F = ¹⁄_r² v = ^v⁄_|v|² is the only incompressible radial field.

  Computing directly:

  div F(x,y)   =   ^∂⁄_∂x(^x⁄_(x²+y²))  +  ^∂⁄_∂x(^y⁄_(x²+y²))

    =   ^{(x2+y2−2x2)} ⁄_(x²+y²)²  +  ^{(x2+y2−2y2)} ⁄_(x²+y²)²   =   0.

  2c. We look visually at the flux of F across the polar box curve:

  

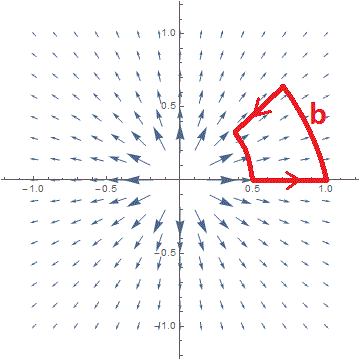
  The flow across the radial segments is zero. The outer circular arc is twice as long as the inner arc, but the field on the outside is half as strong, so outflow balances inflow, and the net outflow is zero: ∮ F(b) • dn = 0.

  Calculating the flux, we use the parametrized segments:

  b₁(t) = ( ½ + ½t, 0 )
  b₂(t) = ( cos(¼πt) , sin(¼πt) )
  b₃(t) = ( ½√2 − ¼√2 t , ½√2 − ¼√2 t )
  b₄(t) = ( ½cos(¼π − ¼πt) , ½sin(¼π − ¼πt) ),

  with 0 ≤ t ≤ 1. The flux across these four segments is: ∮ F(b) • dn   =   ∮ F(b) • (−db^⊥)   =

  ∫¹₀ F(½+½t, 0) • (−(½+½t, 0)')^⊥ dt
   +  ∫¹₀ F(cos(¼πt) , sin(¼πt)) • (−(cos(¼πt) , sin(¼πt))')^⊥ dt
   +  ∫¹₀ F(½√2−¼√2 t, ½√2−¼√2 t) • (−(½√2−¼√2 t, ½√2−¼√2 t)')^⊥ dt
   +  ∫¹₀ F(½cos(¼π − ¼πt), ½sin(¼π − ¼πt)) • (−(½cos(¼π − ¼πt), ½sin(¼π − ¼πt))')^⊥ dt.

  Computing the last term in detail, we start with |(a cos(θ), a sin(θ))| = |a|, so that:
  F(a cos(θ), a sin(θ)) = ¹⁄_|a| (cos(θ), sin(θ)). Then:

  ∫¹₀ F(½cos(¼π − ¼πt), ½sin(¼π − ¼πt)) • (−(½cos(¼π − ¼πt), ½sin(¼π − ¼πt))')^⊥
    =   ∫¹₀ ½ (cos(¼π − ¼πt), sin(¼π − ¼πt)) • (−¼π cos(¼π − ¼πt), −¼π sin(¼π − ¼πt)) dt
    =   −∫¹₀ ^π⁄₈ dt   =   ^−π⁄₈ .

  This confirms our expectation of inflow over the inner circle.

  The Divergence Theorem computes the flux integral right away, as a double integral over the polar box B enclosed by the curve: as ∮ F(b) • dn = ∬_B div F dA = 0, since div F(x,y) = 0 everywhere.

  2d. Visually, the outflow across the unit circle is obviously positive. Calculating, we use c(t) = (cos(t), sin(t)) for 0 ≤ t ≤ 2π. Then:

  ∮ F(c) • dn   =   ∫₀^2π F(cos(t), sin(t)) • (−(cos(t), sin(t))')^⊥ dt
    =   ∫₀^{2π 1}⁄_1² (cos(t), sin(t)) • (−(−sin(t), cos(t)))^⊥ dt
    =   ∫₀^2π (cos(t), sin(t)) • (−(−cos(t), −sin(t))) dt   =   2π.

  2e. The result of part (d) seems to contradict the Divergence Theorem, applied to the unit disk region C and its boundary c:

  2π   =   ∮ F(c) • dn   ≠   ∬_C div F dA   =   0 ?

  But: the integrand of the double integral on the right is not defined everywhere: div F(0,0) = ¹⁄_0² (0,0), which does not exist. In fact, F(x,y) has a point-source of flow from (0,0), which suggests an infinite rate of outflow per unit area. This "infinite value" at a single point is enough to make the double integral non-zero. It is actually possible to make mathematical sense of this statement.

• ⊞ 1/27: Lect 7. Vectors in R² and R³  
  Reading: M&T textbook 1.1 Vectors  1.2 Inner product.
  Do the Weekly HW due 1/29 below.
  HW:

  1. The length of a parametric curve c(t) = (x(t), y(t)) is defined as:
     L   =   lim_n→∞ ∑ⁿ_i=1 |Δc_i| ,

     where c₀,...,c_n are sample points of the curve, and Δc_i = c_i − c_i−1 are short steps along the curve. We can write this symbolically as: L  =  ∮ |dc|.

     1. Figure out a practical formula for L as an ordinary single-variable integral.
        Hint: Approximate Δc_i ≈ c'(t_i) Δt, where c_i = c(t_i), and write the result as an integral ∫ dt.
     2. Describe how this formula generalizes to 3 or higher dimensions.
     3. Find the length of the helix (corkscrew) curve:
        c(t)   =   (cos(t), sin(t), t),     0 ≤ t ≤ 2π.

  2. Consider two plane vectors u = (u₁, u₂), v = (v₁, v₂) ∈ R².
     1. Based on the formula u • v = |u| |v| cos θ_uv and basic trigonometry, show that the length of the perpendicular projection of v to the direction u is ^{|u • v|}⁄_|u| .
     2. Taking u^⊥ = (−u₂, u₁), show that the length of the projection of v in the direction perpendicular to u is ^{|u⊥ • v|}⁄_|u|.
     3. Consider the parallelogram spanned by u and v: that is, the vertices are the origin 0, u, v, and u + v. Find the area of this parallelogram in terms of u, v, and work out the result in terms of the components u_i, v_i .
        Hint: Consider u as the base, determine the height by projecting v perpendicular to u, and take area = base times height.
     4. Would this formula work for space vectors u, v ∈ R³? What would go wrong?
  3. Consider vectors u = (1,2,3), v = (6,5,4) ∈ R³, and let p be the perpendicular projection of u to the direction v. (See M&T p. 25, Orthogonal Projection; also HW 1/11 #2.)
     1. Find the length |p|. Hint: |p| = |u| cos θ_uv, which can be compared to u • v.
     2. Write the vector p. Hint: Scale v to give the length found in part (a).
     3. Write the orthogonal decomposition u = p + q, where p is parallel to v, and q is orthogonal to v. Hint: Solve for q in terms of the known u and p.
     4. If we think of v as a rod with a bead sliding along it, and a string pulls on the bead in direction u with a force of 10 Newtons, what is the component of the force pulling along the rod?

  ⊞ Solutions

  1a.

  L  =  ∮ |dc|  ≈  ∑ⁿ_i=1 |Δc_i|  ≈  ∑ⁿ_i=1 |c'(t_i) Δt|

   =  ∑ⁿ_i=1 |c'(t_i)| Δt  ≈  ∫¹₀ |c'(t)| dt  =  ∫¹₀ √(x'(t)² + y'(t)²) dt,

  where c(t) has parameter 0 ≤ t ≤ 1. As n → ∞, the approximations become equalities, and we get:

  L  =  ∫¹₀ |c'(t)| dt  =  ∫¹₀ √(x'(t)² + y'(t)²) dt.

  1b. The same reasoning and formulas apply to R³ (or Rⁿ), except with more components. The length of c(t) = (x(t), y(t), z(t)) for 0 ≤ t ≤ 1 is:

  L  =  ∫¹₀ |c'(t)| dt  =  ∫¹₀ √(x'(t)² + y'(t)² + z'(t)²) dt.

  1c. The helix curve c(t) = (sin(t), cos(t), t) for 0 ≤ t ≤ 2π goes around the unit circle in the xy-plane, and rises at the same time. It has derivative (velocity vector) c'(t) = (−cos(t), sin(t), 1); and length:

  L  =  ∫₀^2π |c'(t)| dt  =  ∫₀^2π √(cos²(t) + sin²(t)² + 1²) dt  =  ∫₀^2π √2 dt  =  2π√2.

  2a. Let p be the orthogonal projection of v on the direction u, meaning p is parallel to u and the vector q from p to v is orthogonal to u. That is, p, q are the legs of a right triangle with hypotenuse v, so by the definition of cosine: |p| = |v| cos θ_pv = |v| cos θ_uv if θ_uv is an acute angle, and |p| = |v| |cos θ_uv| in general. Now the basic formula u • v = |u| |v| cos θ_uv implies:

  |p|  =  |v| |cos θ_uv|  =  ^{|u • v|}⁄_|u| .

  2b. Letting u^⊥ = (−u₂, u₁), the counterclockwise orthogonal of u, take the role of u in the previous problem, we find that the projection of v to the direction u^⊥ is: q  =  ^{|u⊥ • v|}⁄_|u^⊥|  =  ^{|u⊥ • v|}⁄_|u| , since clearly |u^⊥| = |u|.

  2c. For the parallelogram spanned by plane vectors u, v, the base has length |u|, and the height (the length of the projection of v to the perpendicular direction of u, is |q| = ^{|u⊥ • v|}⁄_|u| by the previous problem. Therefore:

  area  =  (height) (base)  =  ^{|u⊥ • v|}⁄_|u|   |u|  =  |u^⊥ • v|

   =  |(−u₂, u₁) • (v₁, v₂)|  =  |−u₂v₁ + u₁v₂|  =  |u₁v₂ − u₂v₁| .

  We will see that this quantity is the absolute value of the 2 × 2 determinant.

  2d. Projections work the same in 3 or higher dimensions as they do in 2 dimensions. However, a vector u ∈ R³ has no well-defined orthogonal vector u^⊥: there is a whole plane of vectors orthogonal to u, and a circle of orthogonal vectors with the same length |u|. Thus, we cannot compute the height of the parallelogram spanned by u, v, unless we find a way to compute the orthogonal to u within the plane spanned by u, v. (We will accomplish this later using the cross product.)

  3a. This time p is the projection of u on direction v. Since |p| = |u| |cos θ_uv| and u • v = |u| |v| cos θ_uv, we have:

  |p| = ^{|u • v|}⁄_|v| = ^{(1• 6 + 2• 5 + 3• 4)} ⁄ _{√(6² + 5² + 4²)} = ²⁸⁄_√77 .

  Alternatively, recall our definition in Lect 1 that u • v = ± |p| |v|, again giving |p| = ^{|u • v|}⁄_|v| .

  3b. The multiple of v with the correct direction and length is:

  p  =  ^{(u • v)}⁄_|v|   ¹⁄_|v| v  =  ^{(u • v)}⁄_{(v • v)} v  =  ²⁸⁄₇₇ (6,5,4)  =  ⁴⁄₁₁ (6,5,4).

  3c. We have: q  =  u − p  =  ¹⁄₁₁ (−13,2,17). We can check that q is indeed orthogonal to v, because:

  q • v  =  (u − p) • v  =  (u − ^{(u • v)}⁄_{(v • v)} v) • v
   =  (u • v) − ^{(u • v)}⁄_{(v • v)} (v • v)  =  0.

  3d. The ratio of the projected force vector in direction p to the original force in direction u is ^|p|⁄_|u| = ²⁸⁄_14√77 = ²⁄_√77 . Thus, the projected force is ²⁄_√77 10 ≈ 2.28 Newtons. (A Newton is the force needed to accelerate 1 kilogram by 1 meter/second in 1 second.)

• ⊞ 1/29: Lect 8. Inner product, determinant.  
  Reading: M&T 1.2 Inner product  1.3 Determinants. Class notes 1/11, p 5. 
  See the Weekly HW due 2/1 below.
  HW:

  1. Consider the plane in R³ containing the points u = (0,1,1), v = (1,1,2), w = (1,2,0). (As usual, when we define a point by a vector, we mean the endpoint of the standard form vector starting at the origin.)
     1. Find two vectors parallel to the plane, for example from u to v, and from u to w.
     2. Write a parametric formula p(s,t) = (x(s,t), y(s,t), z(s,t)) which gives the points of the plane as s,t vary. Hint: Start at u and move along the two directions from part (a).
     3. Consider the point r = (3,4,5), and determine the function d(s,t) which computes the distance between r and the point p(s,t) on the plane.
     4. Determine the distance from r to the plane, by finding the minimum value of d(s,t). Hint: Find the unique critical point where ∇d(s,t) = (0,0). It is actually easier to work with d(s,t)², which has its minimum at the same (s,t).
  2. Go back and do HW 1/11 #1(d,e) on two-dimensional determinants.
  3. For each triple of vectors u, v, w:
     • Sketch the vectors and the parallelopiped they span.
     • Determine whether they form a right-handed triple: that is can you point your right index finger along u, middle finger along v, thumb along w, so that the thumb is not bent behind or through the plane of the other two fingers.
       

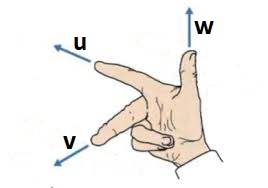
     • Determine the signed volume of the parallelopiped by evaluating the determinant det(u; v; w). Verify that a right-handed triple has positive det, a left-handed one has negative det.
     The triples are:
     1. u = (1,1,0), v = (1,0,1), w = (1,1,2)
     2. u = (1,0,1), v = (1,1,0), w = (1,1,2)
     3. u = (1,1,0), v = (1,0,1), w = (2,1,1)
  ⊞ Solutions

  1a. v−u = (1,0,1), w−u = (1,1,−1).

  1b. p(s,t)  =  u + s(v−u) + t(w−u)  =  (s+t, 1+t, 1+s−t).

  1c. d(s,t)  =  |r − p(s,t)|  =  |(s+t, 1+t, 1+s−t) − (3,4,5)|
   =  √((s+t−3)² + (t−3)² + (s−t−4)²)  =  √(2s²−14s+3t²−4t+34)

  1d. The function D(s,t) = d(s,t)² = 2s²−14s+3t²−4t+34 has its minimum at the same (s,t) as d(s,t). This must occur at a critical point, where:

  ∇D(s,t) = (4s−14, 6t−4) = (0,0)   ⇒   (s,t) = (⁷⁄₂, ²⁄₃).

  Thus, the minimum distance is: d(⁷⁄₂, ²⁄₃) = ⁷⁄_√6.

  2. See solutions for HW 1/11

  3a. The triple u = (1,1,0), v = (1,0,1), w = (1,1,2):

  

  Notice that we draw the x,y,z axes as a right-handed triple, and v is in the xz-plane in the foreground, whereas w recedes into the picture. This is a left-handed system: model it with your left palm up, index finger horizontal along u, middle finger almost vertical along v, thumb pointing away from you along w.

  We compute the determinant, the signed volume of the parallelepiped spanned by the three vectors. We write the rows of a matrix consecutively in one long row, and write v⁽ⁱ⁾ for the vector v with its i^th coordinate omitted.

  det(u;v;w)  =  u₁ det(v⁽¹⁾; w⁽¹⁾) − u₂ det(v⁽²⁾; w⁽²⁾) + u₃ det(v⁽³⁾; w⁽³⁾)

   =  1 det(0,1; 1,2) − 1 det(1,1; 1,2) + 0 det(1,0; 1,1)  =  −1 − 1 + 0  =  −2.

  The negative value verifies the left-handedness.

  3b. The triple u = (1,0,1), v = (1,1,0), w = (1,1,2), with the first two vectors switched from part (a), is right-handed, with the opposite determinant: det(u;v;w) = 2.

  3c. The triple u = (1,1,0), v = (1,0,1), w = (2,1,1) has w = u + v, which means the three vectors all lie in the same plane. Thus, the parallelepiped is flat, with volume zero, and we may verify det(u;v;w) = 0. The triple is degenerate, neither right- nor left-handed.

• ⊞ 2/1: Lect 9. Determinant and cross product.  
  Reading: 1.3 Determinant and cross product. Notes 2/1. See the Weekly HW due 2/5 below.
  HW:

  1. Consider the plane in HW 1/29 #1, passing through the points u = (0,1,1), v = (1,1,2), w = (1,2,0).
     1. Find a vector q orthogonal to this plane. Hint: Take the cross product of two directions in the plane.
     2. Find an equation for the plane in the form ax + by + cz = d. Hint: If p = (x,y,z) is a point of the plane, then p − u is a direction in the plane, orthogonal to q. Write the corresponding dot-product equation, in coordinates.
     3. As in HW 1/29 #1(d), find the distance between the plane and the point r = (3,4,5). Hint: Project r − u on q, obtaining a vector straight from the plane to r.
  2. Recall our definition of determinant for R³: det(u, v, w)  =  u₁ det(v⁽¹⁾; w⁽¹⁾) − u₂ det(v⁽²⁾; w⁽²⁾) + u₁ det(v⁽³⁾; w⁽³⁾), where v⁽ⁱ⁾ represents v with the i^th coordinate omitted; and we use the two-dimensional det(a,b; c,d) = ad − bc.
     1. Expand the above formual for det(u, v, w) into terms of the form u_iv_jw_k. Check that the indices (i,j,k) run over all permutations (rearrangements) of (1,2,3).
        Describe the expansion of the n-dimensional determinant, including the sign of each term.
     2. Show that the determinant is a linear function of the vector u: det(u + u', v, w)  =  det(u, v, w) + det(u', v, w)
        det(su, v, w)  =  s det(u, v, w).
     3. Using the expression from part (a), show that switching two vectors in the determinant gives the negative determinant: det(v, u, w)  =  − det(u, v, w),     det(u, w, v)  =  − det(u, v, w).
     4. Show that det(u, u, w) = 0. Hint: This follows immediately from part (c).
     5. Show that the cross product obeys the Anti-commutative law:  a × b = − b × a.  Also:  a × a = 0.
  ⊞ Solutions

  1a. The cross product of two vectors is orthogonal to them both. Thus:

  q = (v−u) • (w−u) = (1,0,1) × (1,1,−1) = (−1,2,1).

  1b. Every direction along the plane is orthogonal to q from part (a). Thus, the vector from u to an arbitrary point p = (x,y,z) in the plane is orthogonal to q:

  q • (p−u) = 0   ⇔   (−1,2,1) • (x, y−1, z−1) = 0
    ⇔   −x + 2y + z = 3

  1c. The vector r − u = (3,4,5) − (0,1,1) = (3,3,4) points at an angle from the plane to r; the "height" of this vector (i.e. the component orthogonal to the plane) is the distance from the plane to r. To get the length of the projection of r − u on the orthogonal direction q, we take the dot product with the unit vector ^q⁄_|q|:

  ^{|(r−u) • q|}⁄_{|q|  =  ^{|(3,3,4) • (−1,2,1)|}⁄|(−1,2,1)|  =  ⁷⁄√6,}

  which agrees with the result from HW 1/25 #2(d).

  2a. Expanding the definition of the determinant gives:

  det(u, v, w)  =  u₁v₂w₃ − u₁v₃w₂ − u₂v₁w₃ + u₂v₃w₁ + u₃v₁w₂ − u₃v₂w₁

  Note that the subscripts of the terms u_iv_jw_k are (i,j,k) = (1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1). These are all 3! = 3•2•1 = 6 ways of rearranging (1,2,3).

  For a higher dimension n, there are n! ways of permuting n distinct objects, which we encode as one-to-one functions π from {1,...,n} to itself. Examples: the identity mapping π(i) = i; or the flip-over mapping π(i) = n+1−i. Consider n vectors u₁,..., u_n, with coordinates u_i = (u_i1,...,u_in). Their determinant is:

  det(u₁,..., u_n)   =   ∑_π sgn(π) u_1,π(1) ... u_n,π(n) ,
  where sgn(π) = +1 if π can be produced from the identity permutation with an even number of switches of adjacent elements, and −1 if an odd number.

  2b. We compute:

  det(u + u', v, w)  =  (u₁ + u'₁) det(v⁽¹⁾; w⁽¹⁾) − (u₂ + u'₂) det(v⁽²⁾; w⁽²⁾) + (u₃ + u'₃) det(v⁽³⁾; w⁽³⁾)

   =  ( u₁ det(v⁽¹⁾; w⁽¹⁾) − u₂ det(v⁽²⁾; w⁽²⁾) + u₃ det(v⁽³⁾; w⁽³⁾) )
            +  ( u'₁ det(v⁽¹⁾; w⁽¹⁾) − u'₂ det(v⁽²⁾; w⁽²⁾) + u'₃ det(v⁽³⁾; w⁽³⁾) )

   =  det(u, v, w) + det(u', v, w)

  Similarly for det(su, v, w)  =  s det(u, v, w).

  2c. Switching u, v in the input of det, we get:

  det(v, u, w)
   =  v₁u₂w₃ − v₁u₃w₂ − v₂u₁w₃ + v₂u₃w₁ + v₃u₁w₂ − v₃u₂w₁
   =  u₂v₁w₃ − u₃v₁w₂ − u₁v₂w₃ + u₃v₂w₁ + u₁v₃w₂ − u₂v₃w₁
   =  −det(u, v, w),

  since on the third line, each term appears with the opposite sign as in det(u, v, w). The other formula is similar.

  2d. We can check this formula directly from the expansion as in part (c), but there is an easier way. If we use the part (c) formula det(v, u, w) = −det(u, v, w), and replace v with u, we get:

  det(u, u, w) = −det(u, u, w).

  But a = −a means 2a = 0 and a = 0, and so det(u, u, w) = 0.
  The same argument shows det(u, v, v) = 0 and det(u, v, u) = 0.

  2e. Again, we can check this directly as in part (c), but there is an easier way. If we use the formula which motivated the cross-product, det(u, v, w) = (u × v) • w, we find:

  (v × u) • w = det(v, u, w) = −det(u, v, w) = −(u × v) • w.

  But if a × w = b × w for every vector w, then a = b, so v × u = − u × v.

• ⊞ 2/3: Lect 10. Limits and derivatives for f(x,y).  
  Reading: 2.1 Real-valued functions 
  Notes 2/1.  See the Weekly HW due 2/5 below.
  HW:

  1. Menagerie of functions. For each of the following f : R² → R, determine the following properties:
     • Is f continuous at (0,0), meaning lim_{(x,y)→(0,0)} f(x,y) = f(0,0)?
     • Is f continuous at (0,0) on each line (x,y) = t(a,b) for t ∈ R?
     • Is f differentiable at (0,0), meaning it has a tangent plane which approaches the graph very closely?
     • Is f differentiable at (0,0) on each line (x,y) = t(a,b), meaning it has a directional derivative ^d⁄_dt f(ta,tb)|_t=0 ?
     The functions are:
     1. f(x,y) = ^2xy⁄_(x²+y²) , and f(0,0) = 0. This is a "staircase" or radially constant function, meaning f(sv) = f(v) for s ≠ 0.
     2. f(x,y) = ^x(x2−3y2)⁄_(x²+y²) , and f(0,0) = 0. This is a homogeneous function, meaning f(sv) = s f(v) for s ∈ R.
     3. f(x,y) = 1 when x > 0 , 0 < y < x²; and f(x,y) = 0 otherwise. The graph has a plateau above the very sharp region under the parabola and above the positve x-axis.
     Hints: To visualize graphs (a) and (b), look at their values for (x,y) = (cos(θ), sin(θ)) on the unit circle, which determine the rest. Function (b) actually has f(cos(θ), sin(θ)) = sin(3θ). To see their properties on each line, examine the single-variable functions g(t) = f(ta, tb).
  ⊞ Solutions

  1a. f(x,y) is not continuous at (0,0), since there is no way to guarantee f(x,y) is close to f(0,0) = 0, no matter how close (x,y) is to (0,0). For example, f(t,t) = 1 no matter how small t is.
  Furthermore, g(t) = f(ta,tb) is continuous only if (a,b) = (a,0) or (0,b); however, any g(t) = f(ta,tb) ^2ab⁄_√(a²+b²) is constant outside t = 0, so it has a removable discontinuity, meaning g(t) would be continuous if we changed g(0) to the constant value. However, there is no way to change f(0,0) to make f(x,y) continuous.
  Since f(x,y) is not continuous at (0,0), it cannot be differentiable either. Also, g'(0) = 0 for all t ≠ 0.

  1b. f(x,y) is continuous at (0,0), and hence at (0,0) on every line (x,y) = (ta,tb).
  Also, every g(t) = f(ta,tb) = (^a(a2−3b2)⁄_√(a²+b²)) t is a linear function of t, and has a derivative at t = 0.
  However, f(x,y) is not differentiable at (0,0) since the radial tangent lines wave up and down too much, and do not fit into a tangent plane.

  1c. f(x,y) is not continuous at (0,0) since f(t, ½t²) = 1 ≠ f(0,0) = 0, no matter how small t > 0; and hence f(x,y) is not differentiable at (0,0) either. However, g(t) = f(ta,tb) = 0 for |t| ≤ ^b⁄_a , so g(t) = 0 in a neighborhood of t = 0 for any (a,b), and g(t) is both continuous and differentiable at t = 0 for any (a,b).

• ⊞ 2/5: Lect 11. Limits, derivatives of f(x₁,...,x₁) 
  Reading: Class notes.  Ch 2.2 Limits and Continuity (ε-δ method) pp. 94−102  Ch 2.3 Differentiation 
  HW: Give epsilon-delta (error control) proofs of the following.

  1. Composition of continuous functions: If f : Rⁿ → R is continuous at x = c, and g : R → R is continuous y = f(c), then the composite function g(f(x)) is continuous at x = c.
     Hint: Given that 0 < |x − c| < δ' can be chosen to guarantee |f(x) − f(c)| < ε' for any ε', and 0 < |y − f(c)| < δ can be chosen to guarantee |g(y) − g(f(c))| < ε for any ε, you must find a small enough input error δ" so that |x − c| < δ" guarantees |g(f(x)) − g(f(c))| < ε.
  2. Differentiation Product Rule. If the functions f,g : Rⁿ → R are differentiable at x = c, then the product function f(x)g(x) has the following derivative function:
     D(fg)_c(x)  =  f(c) Dg_c(x) + g(c) Df_c(x) .

     Hint: Given that lim_x→c ^{|f(x) − f(c) − Df_c(x−c)|}⁄_|x−c| = 0, and similarly for g(x), you must show that the proposed derivative function is close to f(x)g(x), relative to |x − c|.

  3. Directional derivative. For f : Rⁿ → R and v ∈ Rⁿ, define the directional derivative:
     ^∂f⁄_∂v(c)  =  ^d⁄_dt f(tv)|_t=0  =  lim_t→0 ^{(f(c+tv) − f(c))}⁄_t .
     1. If f is differentiable at x = c, then ^∂f⁄_∂v(c)  =  Df_c(v).
        Note that we proved in class that Df_c(v) = ∇f(c) • v.
     2. The slope of f(x) in direction v is ∇f(c) • ^v⁄_|v|.
     3. The maximum directional slope ∇f(c) • ^v⁄_|v| is in the direction v = ∇f(c), and the value of this slope is the magnitude |∇f(c)|. This proves that ∇f(c) is the uphill direction, and its magnitude is the maximum slope.
  ⊞ Solutions

  1. See Notes §4.

  2. See Notes §8. Actually, this is probably too hard for an exercise.

  3a. By the definition of derivative, we have:

  0  =  |v| lim_t→0 ^{|f(c+tv) − f(c) − ∇f(c)•tv|}⁄_|tv|  =  lim_t→0 | ^{(f(c+tv) − f(c))}⁄_t − ∇f(c)•v | .

  This is equivalent to:

  ^∂f⁄_∂v(c)  =  lim_t→0 ^{(f(c+tv) − f(c))}⁄_t  =  ∇f(c) • v.

• ⊞ 2/8−10: Lect 12−13. Differentiation and properties of the derivative 
  Reading: 2.3 Differentiation  2.4 Paths and Curves  2.5 Properties of the Derivative 
  HW: From Marsden & Tromba

  1. Find the following limits lim_{(x,y)→(0,0)} f(x,y), if they exist.   Hints:
     • Freely use known facts about one-dimensional limits, such as L'Hopital's Rule.
     • Ignore points where f(x,y) is undefined: we only care whether the defined values approach a limit.
     • If we can write f(x,y) = g(h(x,y)), where g(t) is a one-variable function, the limit can be reduced to computing lim_{(x,y)→(a,b)} h(x,y) = L, then lim_t→L g(t).
     • To show a limit does not exist, find two curves (x(t), y(t)) such that f(x(t), y(t)) approaches different values as (x(t), y(t)) → (0,0).
     Take limits of the following functions:
     1. (p 103 #9)   f(x,y) = ^{(exy − 1)}⁄_y
     2. (p 103 #9)   f(x,y) = ^{(cos(xy) − 1)}⁄_x²y²
     3. (p 103 #6)   f(x,y) = ^xy3⁄_x²+y⁶   (Examine (x(t), y(t)) = (t,0) and (t³, t).)
     4. (p 103 #10)   f(x,y) = ^(x−y)2⁄_x²+y²
  2. (p 115 #7) Consider the tangent plane P of the graph z = f(x,y) = e^x−y above the point (x,y) = (1,1).
     1. Find an equation for P of the form z = a + bx + cy. Hint: Write the graph of the affine approximation to f(x,y) near (x,y) = (1,1), and simplify.
     2. Find a vector q orthogonal to the plane P (that is, orthogonal to any vector between two points of P). Hint: Write the equation for P in the form (x,y,z) • q = d. Why is this q orthogonal to P?
  3. (p 115 #16)   Use an affine approximation for the function f(x,y,z) = (x² + y² + z²)^1/2 to find an accurate esimate of the number: = ((4.01)² + (3.98)² + (2.02)²)^1/2
  4. (p 124 #24)   Consider the exponential spiral given by: c(t) = (e^t cos(t), e^t sin(t)). Show that the angle between the radial vector c(t) and the velocity vector c'(t) is constant for all t.
     This is why a moth flies in a spiral path around a flame: it is trying to navigate in a straight line by keeping the moon or a star at a constant angle in its field of vision.
  5. (p 133 #13)   Suppose a duck is swimming in the circular path c(t) = (cos(t), sin(t)), and the water temperature is given by T(x,y) = x²e^y − xy³. Find ^dT⁄_dt in two ways: by the Chain Rule for T(c(t)), and by writing out the formula for f(t) = T(c(t)) and directly differentiating.
  6. (p. 142 #4)   You are walking on a hillside in the shape of the graph z = y cos(πx) − x cos(πy) + 10, standing at the point (2,1,13). Find an xy-vector direction you can walk so as to stay at the same level, a vector pointing along a contour. (How is this related to the uphill direction?)
  7. Consider the function f : R³ → R given by f(x,y,z) = x² + 2y² + 3z².
     1. Describe the level surface S ⊂ R³ defined by f(x,y,z) = d, for a given constant d. (The level surface of a three-variable function is the analog of the level curve (contour) of a two-variable function.)
        Hint: Consider the points with x² + y² + z² = d, and modify the y- and z-coordinates to get f(x,y,z) = d.
     2. Find the equation of the tangent plane to the surface f(x,y,z) = 13 at the point (1,0,2).
        Hint: How does the level surface relate to the gradient vector ∇f(1,0,2), the direction of fastest increase of f? See M&T p. 139.
  8. Theorem: Consider the function f : R³ → R with the level surface S = {(x,y,z) with f(x,y,z) = d}. Suppose c(t) = (x(t), y(t), z(t)) is a curve contained in the surface S, with c(0) = (a,b,c). Then the tangent vector c'(0) is orthogonal to the gradient ∇f(a,b,c). Thus, the level surface S is orthogonal to the gradient.
     Prove this Theorem by applying the Chain Rule to f(c(t)).

  ⊞ Solutions.

  Answers to odd-numbered problems are in M&T pp 502−506.

  1a. f(x,y)  =  ^{(exy − 1)}⁄_y  =  ^{x (exy − 1)}⁄_xy  =  ^{x (et − 1)}⁄_t , where t = xy. Since lim_t→0 ^{(et − 1)}⁄_t  =  1 by L'Hopital's Rule, we have lim_{(x,y)→(0,0)} f(x,y) = (0)(1) = 0.

  1b. Again taking t = xy and using L'Hopital twice gives lim_{(x,y)→(0,0)} f(x,y)  =  ^{(cos(t) − 1)}⁄_t²  =  −½.

  1c. Consider f(t,0) = 0, and f(t³, t) = ^t6⁄_2t⁶ = ½. Thus no matter how close (x,y) is to (0,0), there are values of f(x,y) equal to 0, and others equal to ½, so f(x,y) does not approach a single limit value.

  1d. We take f(t,t) = 0, and f(t, −t) = ^(2t)2⁄_2t² = 2, so again f(x,y) does not approach a single limit value as (x,y) → (0,0).

  2a. For f(x,y) = e^x−y, we have: ^∂f⁄_∂x|_(x,y)=(1,1) = 1, and ^∂f⁄_∂y|_(x,y)=(1,1) = −1, so the affine approximation is:

  f(x,y)  ≈  f(1,1) + ^∂f⁄_∂x (x−1) + ^∂f⁄_∂y (y−1)  ≈  1 + (x−1) − (y−1)  ≈  1 + x − y

  and the tangent plane is: z = 1 + x − y.

  2b. The equation of P can be written as: −x + y + z = 1, i.e. (x,y,z) • (−1, 1, 1) = 1. Thus q = (−1, 1, 1) is orthogonal to the plane. Indeed, any two points v, v' on the plane satisfy v • q = v' • q = 1 so the vector v −v' between them, a vector parallel to the plane, has (v−v') • q = 1−1 = 0.

  3. For (x,y,z) = (4.01, 3.98, 2.02) near (4,4,2), we have the affine linear approximation f(x,y,z)  ≈  f(4,4,2) + ∇f(4,4,2) • (x−4, y−4, z−2)  ≈  6 + (²⁄₃, ²⁄₃, ¹⁄₃) • (x−4, y−4, z−2)  =  6 + ²⁄₃(x−4) + ²⁄₃(y−4) + ¹⁄₃(z−4)  =  6 + ²⁄₃(0.01) + ²⁄₃(−0.02) + ¹⁄₃(0.02).

  4. The curve c(t) = e^t (cos(t), sin(t)) has derivative (velocity vector, tangent vector) given by the product rule:

  c'(t)  =  (e^t)' (cos(t), sin(t)) + e^t (cos(t), sin(t))'
   =  e^t (cos(t)−sin(t), sin(t)+cos(t)),

  and we have |c(t)| = e^t, and |c'(t)| = e^t √2. A constant angle between c(t) and c'(t) would mean a constant dot product between the corresponding unit vectors:

  cos θ_cc'  =  ^c⁄_|c| • ^c'⁄_|c'|
   =  (cos(t), sin(t)) • ¹⁄_√2 (cos(t)−sin(t), sin(t)+cos(t))  =  ¹⁄_√2 .

  Thus θ_cc' = ±^π⁄₄ .
  The moth would go inward along the path c(−t) with tangent −c'(−t), and it would see the flame at the origin in the direction −c(−t), which would give the same constant angle ^π⁄₄ .

  5. For a function T(x,y) and a curve c(t) = (x(t), y(t)), the Chain Rule says:

  ^dT⁄_dt   =   ^d⁄_dt T(c(t))   =   ∇T(c(t)) • c'(t)   =   ^∂T⁄_∂x ^dx⁄_dt  +  ^∂T⁄_∂y ^dy⁄_dt .

  Plugging in the given functions to this formula gives the same result as first plugging in to get f(t) = T(c(t)), and then using the one-variable Chain Rule to compute f '(t).

  6. In the graph, z = f(x,y), the gradient ∇f(a,b) in the xy-plane points in the uphill direction from (a,b), which is always orthogonal to the contour curve (level curve) C = {(x,y) with f(x,y) = f(a,b)}. Thus, the orthogonal vector ∇f(a,b)^⊥ points along the C at (a,b). Note: ∇f(a,b) has a unique orthogonal direction because it is a vector in the plane R². (A three-dimensional vector has a whole plane of orthogonal vectors.)

  7a. The points (x,y,z) with x² + y² + z² = d form the sphere with radius √d from the origin. Squeezing these points to (x, ^y⁄_√2, ^z⁄_√3) gives the solutions to f(x,y,z) = d, namely the level surface S. Thus S is an ellipsoid: a sphere flattened by a factor of ¹⁄_√2 in the y direction, and by ¹⁄_√3 in the z direction.

  7b. The gradient ∇f(a,b,c) ∈ R³ points in the direction of fastest increase of f(x,y,z), starting from (a,b,c). This is orthogonal to the directions of no increase, namely the tangents to the level surface. (Thinking of f(x,y,z) as temperature, the gradient points in the hottest direction, which is orthogonal to the directions of constant temperature.)

  The plane orthogonal to q and passing through the point p is given by v = (x,y,z) satisfying q • (v−p) = 0, or equivalently q • v = q • p. Thus, the equation of the tangent plane to S is given by:

  ∇f(a,b,c) • (x,y,z)   =   ∇f(a,b,c) • (a,b,c)

  2ax + 4by + 6cz  =  2a² + 4b² + 6c².

  For (a,b,c) = (1,0,2), this is 2x + 12z = 26.

  8. Theorem: If a curve c(t) = (x(t),y(t),z(t)) goes along a level surface of the function f(x,y,z), then the tangent c'(t) is orthogonal to the gradient ∇f(c(t)).

  Proof: By hypothesis, we assume f(c(t)) = a for all t and some constant a. Differentiating the left side by the multivariable Chain Rule gives:

  ^d⁄_dt f(c(t))   =   ^d⁄_dt( a )

  ∇f(c(t)) • c'(t)   =   0.

  This confirms that the gradient is orthogonal to the tangent, as desired.

• ⊞ 2/12: Lect 14. Linear mappings, matrix notation, Jacobian matrix  
  Reading: Class notes. Ch 1.5 pp 63−65, Ch 2.3 pp 111−113.
  HW:

  1. Linear mappings for R and R².
     1. Write the 1×2 matrix of the linear mapping ℓ(x,y) = 2x + 3y. The columns of this matrix are just the numbers ℓ(i) = ℓ(1,0) and ℓ(j) = ℓ(0,1). Check that [ℓ(v)] = [ℓ] • [v].
     2. What is a general formula for a linear mapping ℓ : R → R² ? What is its matrix like?
     3. What is a general formula for a linear mapping ℓ : R → R? What is its matrix like?
  2. Consider the dilation mapping ℓ : Rⁿ → Rⁿ given by ℓ(v) = av for a given constant scalar a.
     1. Check that ℓ is a linear mapping.
     2. Find the matrix [ℓ].
  3. For each of the following matrices, geometrically describe the corresponding linear mapping.

     a.

     0   1   1   0

     b.

     3   0   0   3

     c.

     1   1   0   1

     d.

     1   1   0   1   1   0

     e.

     0   0   1   1   0   0   0   1   0

     Hint: For (c), describe how the mapping distorts the unit square into the parallelogram spanned by ℓ(i) and ℓ(j); this is called a shear mapping. For (d) and (e), determine the dimensions of the input and output spaces, and again consider the outputs of the standard basis vectors.
  4. Consider the spherical coordinate map s : R³ → R³, which takes the coordinates (ρ, θ, φ) to a point with radius ρ (altitude); angle θ from the positive x-axis, rotating around the z-axis (longitude); and angle φ from the z-axis (the complementary angle of latitude). Note: ρ = rho, θ = theta, φ = phi.
     1. Show that:
        s(ρ, θ, φ)  =  ( ρ sin(φ) cos(θ), ρ sin(φ) sin(θ), ρ cos(φ) ).
        Hint: For a vector with length ρ and angle φ from the z-axis, the height (z-coordinate) is ρ cos(φ); and the radius from the positive z-axis is r = ρ sin(φ). To get longitude θ, the projection onto the xy-plane is (r cos(θ), r sin(θ)), as in polar coordinates.
     2. Compute the Jacobian matrix of partial derivatives at c = (ρ, θ, φ):
        [Ds_c]  =  [ ^∂s⁄_∂ρ | ^∂s⁄_∂θ | ^∂s⁄_∂φ ],
        whose columns are the partial derivatives of s(ρ, θ, φ), written vertically in matrix notation.
     3. Explicitly write the affine linear approximation of s(v) for v = (ρ, θ, φ) near c = (2, π, ⅓π):
        s(v)  ≈  s(c) + Ds_c(v − c).
        Give the (x,y,z)-coordinates of the output.
  ⊞ Solutions 

  1a. Since ℓ : R² → R¹, its matrix [ℓ] has 1 row, 2 columns. We have ℓ(1,0) = 2, ℓ(0,1) = 3, so [ℓ] = [ℓ(i) | ℓ(j)] = [2,3]. To get back the function, we perform matrix multiplication: [ℓ(v)] = [ℓ]•[v] = [2,3]•[x,y]^T = 2x + 3y, which is the same as dot product of the row (2,3) with the vector v = (x,y).

  1b. A linear mapping ℓ : R¹ → R² has a matrix [ℓ] with 2 rows, 1 column. The most general such mapping, corresponding to a column matrix [a,b]^T, is ℓ(x) = (ax, bx).

  1c. A linear mapping ℓ : R → R is just ℓ(x) = ax, with matrix [a].

  2. The matrix of ℓ : Rⁿ → Rⁿ has n rows, n columns, given by [ℓ(e₁) | ... | ℓ(e_n)]. Since ℓ(e_i) = ae_i , this means every entry of [ℓ] is zero, except the entry in the i^th row, i^th column is a. This is called a diagonal matrix.

  3. Matrices (a), (b), (c) all give mappings ℓ : R² → R².

  3a. ℓ switches the basis vectors i and j in the plane, and ℓ(x,y) = (y,x). Geometrically, this is a reflection across the line y = x.

  3b. ℓ stretches each basis vector by a factor of 3, and ℓ(x,y) = (3x, 3y), so ℓ stretches every vector the same way: ℓ(v) = 3v. This is a dilation.

  3c. ℓ(i) = i and ℓ(j) = (1,1) = i + j. The mapping squeezes the rectangular grid into the lopsided grid with lines parallel to i and i + j.

  3d. A matrix with 3 rows, 2 columns gives ℓ : R² → R³, and matrix multiplication gives ℓ(x,y) = x(1,0,1) + y(1,1,0). You can picture this as sending the grid in R² to a plane in R³ with grid lines parallel to (1,0,1) and (1,1,0).

  3e. We have ℓ : R³ → R³ with matrix [ℓ] = [j | k | i], so ℓ(i) = j , ℓ(j) = k , ℓ(k) = i , and matrix multiplication gives ℓ(x,y,z) = (z,x,y). Picturing what this does to the triangle with corners at i, j, k, we see this is a ⅓ rotation around the axis (1,1,1) going through the center of the triangle.

  4a. See M&T pp 54−58, or this website.

  4b. [ Ds_(ρ,θ,φ) ] is:
  
  

  sin(φ) cos(θ)	−ρ sin(φ) sin(θ)	ρ cos(φ) cos(θ)
  sin(φ) sin(θ)	ρ sin(φ) cos(θ)	ρ cos(φ) sin(θ)
  cos(φ)	0	−ρ sin(φ)

  Plugging in (ρ,θ,φ) = (2, π, ⅓π) gives:
  
  

  −√3⁄2	0	−1
  0	−√3	0
  1⁄2	0	−√3

  4c. Multiplying [ Ds_(x,y,z) ] • [ρ, θ, φ]^T:
  
  

  −√3⁄2	0	−1		ρ		−√3⁄2 ρ + (−1) φ
  0	−√3	0	•	θ	=	−√3 θ
  1⁄2	0	−√3		φ		1⁄2 ρ + (−√3) φ

  Thus:

  s(ρ, θ, φ)  ≈  s(2, π, ⅓π) + Ds_{(2, π, ⅓π)}(ρ−2 , θ−π , φ−⅓π)
   =  (−√3, 0, 1) + (^−√3⁄₂(ρ−2) + (−1)(φ−⅓π) , −√3(θ−π) , ¹⁄₂(ρ−2) + (−√3)(φ−⅓π))
   =  ( − ^√3⁄₂ ρ − φ + ^π⁄₃ , −√3 θ + π√3 , ¹⁄₂ ρ − √3 φ + ^√3⁄₃ π ).

• ⊞ 2/15−17: Lect 15−16. Matrix multiplication and Chain Rule for general functions 
  Class notes.
  HW:

  1. For each of the linear mappings ℓ : R² → R² below, find the matrix [ ℓ ] = [ ℓ(i) | ℓ(j) ] .
     1.  r₁(x,y) = (−x,y), reflection across the y-axis.
     2.  r₂(x,y) = (y,x), reflection across the line y = x.
     3. The composite mapping r₁ ∘ r₂, doing r₁ after r₂. Do this both from the definition r₁(r₂(x,y)), and by multiplying the matrices from (a) and (b).
     4. The opposite composition r₁ ∘ r₂. Is composition (and matrix multiplication) a commutative operation?
     5.  R_θ , rotation by angle θ counterclockwise.
     6.  R_α ∘ R_β , the composite of rotating by angle β, then by α.
     7. Geometry tells us the result of part (f) must be the same as R_α+β. Equate the two matrices to prove the angle sum identities in trigonometry.
  2. Suppose we are given some mappings f : R² → R²,   c : R → R², and  g : R² → R.
     1. Form all possible compositions between these functions, in which the output of one must be a suitable input for the other. In each case, write out the Chain Rule for functions of the given dimensions, specifying the entries of the product Jacobian matrix.
     2. Now suppose the functions are defined by:
        f(x,y) = e^x2+y2 (x,y),    c(t) = (t cos(t), t sin(t)),    g(x,y) = x² + y².

        Examine the graphs of a couple of the possible compositions, and try to make sense of them. Check the Chain Rule in by evaluating the composition directly and finding its derivative; then computing the product of Jacobian matrices, and comparing.

  Solutions

• ⊞ 2/20−22: Lect 17−18. 3.1 Iterated Partial Derivatives   3.2 Taylor Series   3.3 Extrema  
  HW:

  1. Consider an iron bar marked with the position coordinate x ≥ 0, and let f(x,t) denote the temperature of position x at time t. The Heat Equation is a partial differential equation (i.e. a differential equation involving partial derivatives) which models the flow of heat in the bar: the temperature f(x,t) must satisfy:
     ^∂f⁄_∂t   =   ^∂2f⁄_∂x²
     Problem: Show that f(x,y) = ¹⁄_√t exp(− ^x2⁄_4t) is a solution to the Heat Equation. Graph some slices z = f(x,t) above t = 0.1, 0.5, 1.0, 2.0 to see how the heat dissipates from a point-source at x = 0.
  2. (Ch 3.1 p 157 #18) For f(x,y,z) = z e^xy + x²yz³, verify that:
     ^∂3f⁄_∂x∂y∂z   =   ^∂3f⁄_∂z∂y∂x
     
  3. (Ch 3.2 p 166 #11) Find the second-order Taylor polynomial (quadratic approximation) at (x,y) = (½π, 1) for the function:
     f(x,y)  =  sin(xy) − 3x² log(y) + 1.

  4. (Ch 3.3 p 182 #5, 9, 19) Find the critical points of the following functions, and use the Hessian to classify them as maximum, minimum, saddle, or degenerate.
     e^1+x2−y2   ,   cos(x²+y²)
     ¹⁄₃ x³ + ¹⁄₃ y³ − ¹⁄₂ x² − ⁵⁄₂ y² + 6y + 10.
     Verify your conclusions by inspecting the contour plots or graphs of these functions. (This is the easiest way to classify the critical points, but it is only possible for two variables.)
  5. The Positive-Definiteness Criterion (Lemma 2, p. 174−176) says that, if we have a quadratic function defined by a Hessian matrix:

     q(x,y)   =   [x,y] •

     a     b     b     c

     • [x,y]T   =   ax2 + 2bxy + cy2,

     
     then q(x,y) is positive-definite, meaning q(0,0) = 0 and q(x,y) > 0 for (x,y) ≠ (0,0), whenever a > 0 and det(H) = ad − bc > 0.
     Prove this by completing the square to get:
     q(x,y)   =   a(x + ^b⁄_a y)²  +  ^(ac−b2)⁄_a y².
     For what a,b,c is this always positive?
  ⊞ Solutions

  1. See M&T p. 156, Example 6.

  3. See p. 509. Correction for #19: For f(x,y) = ¹⁄₃ x³ + ¹⁄₃ y³ − ¹⁄₂ x² − ⁵⁄₂ y² + 6y + 10, the critical points are classified as:

  (0,3) saddle,   (1,2) saddle,   (0,2) max,   (1,3) min.
  Thanks to Marco Macias.

  4. See p. 510.

  5. See p. 175.

• ⊞ 2/24: Lect 19. 3.4 Constrained Extrema, Lagrange Multipliers.
  HW:

  1. Let f(x,y) = x² + xy + y² + x + y.
     1. Find the critical points of f(x,y), and classify them using the Hessian. Determine the maximum and minimum values of f(x,y) on R².
     2. Find the extrema (max/min) points of f(x,y) constrained to the curve g(x,y) = x² + y² = 1. Use Lagrange multipliers to reduce the problem to a system of equations in variables x, y, λ: g(x,y) = 1,   ∇f(x,y) = λ∇g(x,y). Finally, determine which of the local extrema is the absolute max and min.
     3. Redo part (a) with a parametric description of the curve S, given by c(t) = (sin(t), cos(t)) for 0 ≤ t ≤ 2π. That is, find each local extremal point t = a of the one-variable function h(t) = f(c(t)), then take c(a) as a constrained extremal point of f(x,y).
     4. Use the Chain Rule to explain why the equation h'(t) = 0 in part (b) gives a minimum point (x₀,y₀) = c(a) where ∇f(x₀,y₀) is parallel to ∇g(x₀,y₀), as in part (b). Hint: Use the Chain Rule on the equation g(c(t)) = 1 for all t.
     5. Using the previous parts, find the absolute max and min points of f(x,y) on the disk x² + y² ≤ 1. (Consider the interior region and the boundary circle separately.)
  2. (Redo HW 1/13 #5) Consider a rectangular bin having a bottom but no top, and three sides with the fourth side open. Assuming it has volume 1, find the values of (x,y,z), the length, width and height, which will minimize the total surface area of the three sides and bottom. That is, minimize the area function f(x,y,z) constrained to the level surface S given by the volume function g(x,y,z) = 1; use Lagrange multipliers. (We did this in HW 1/13 #5, by parametrizing the surface S as the graph z = 1/xy, and minimizing f(x,y,1/xy) on the region x,y > 0.)
  ⊞ Solutions

  1a. The critical points are defined by ∇f(x,y) = (2x+y+1, x+2y+1) = (0,0). Solving this linear system of equations gives (x,y) = (−⅓, −⅓). The Hessian is:

  Hf(x,y)   =

  2     1     1     2

  ,

  
  which is the same at the critical point: H = H_f(−⅓, −⅓). The leading principal minors det H₁ = 2 and det H₂ = (2)(2)−(1)(1) = 3 are both positive, so H is positive definite, and f has a local minimum (hole) at this point, which must be the absolute minimum point. There is clearly no absolute maximum, since f(x,y) → ∞ as |(x,y)| → ∞.

  1b. We solve ∇f(x,y) = λ ∇g(x,y) and g(x,y) = 1. That is:

  2x + y + 1 = 2λx,   x + 2y + 1 = 2λy,   x² + y² = 1.

  Clearly λ = 0 is not a solution, since this would mean ∇f(x,y) = (0,0), giving the critical point we found in part (a), which does not lie on x² + y² = 1. Thus, we may divide the first two equations, giving ^(2x+y+1)⁄_x+2y+1  =  ^x⁄_y . Cross-multiplying gives y² − x² + y − x = 0, which factors as (y−x)(y+x+1) = 0, giving solutions y = x or y = −x−1.
  If y = x, the equation x² + y² = 1 gives (x,y)  =  ±(¹⁄_√2, ¹⁄_√2) .
  If y = −x−1, the equation x² + y² = 1 gives (x,y)  =  (0, −1) or (−1, 0)
  Evaluating f(x,y) on these 4 critical points gives:

  f(¹⁄_√2, ¹⁄_√2) ≈ 2.9,   f(−¹⁄_√2, ¹⁄_√2) ≈ 0.1,   f(0, −1) = f(−1, 0) = 0.
  Thus, the last two are the constrained absolute minimum points of f(x,y), and the first is the constrained absolute maximum point.

  1c. To find the critical points of:

  h(t)  =  cos²(t) + cos(t) sin(t) + sin²(t) + cos(t) + sin(t)
   =  1 + cos(t) sin(t) + cos(t) + sin(t),
  we solve h'(t) = −sin² + cos²(t) − sin(t) + cos(t) = 0. We can rewrite this as: −1 + 2cos²(t) + cos(t) = ±√(1−cos²(t)). Substituting x = cos(t), we have: 2x² + x − 1 = √(1−x²), which leads to: x(x−1)(2x²+1) = 0, giving the same (x,y) = (cos(t), sin(t)) as in part (a).

  1d. We show how minimizing f(x,y) over the parametrized constraint curve c(t) = (cos(t), sin(t)) leads to the Lagrange Multiplier method, in which we consider the curve as a contour of g(x,y) = x² + y².
  To minimize h(t) = f(c(t)), we solve 0 = h'(t) = ∇f(c(t)) • c'(t). For a solution t = a with c(a) = (x₀,y₀), we have ∇f(x₀,y₀) orthogonal to c'(a), the tangent direction of the circle S at (x₀,y₀).
  On the other hand, the circle is defined by g(x,y) = x² + y² = 1, so we have g(c(t)) = 1. Differentiating this and using the Chain Rule gives: ∇g(c(t)) • c'(t) for all t, including t = a, so that ∇g(x₀,y₀) is also orthogonal to the tangent direction c'(a). Since both ∇f(x₀,y₀) and ∇g(x₀,y₀) are orthogonal to the same direction in R², they must be parallel.

  1e. Evaluate f(x,y) both at the critical points found in part (a), and at the constrained extrema found in part (b) or (c). The largest/smallest of these gives the absolute max/min of f(x,y) within the disk. This is the two-dimensional version of finding the max/min of a single-variable function f(x) on an interval x ∈ [a,b] by finding critical points of f(x) inside the interval, then comparing to the endpoint values f(a), f(b).
  Answer: the absolute minimum is at the interior critical point (−⅓, −⅓); the absolute maximum is at the boundary point (¹⁄_√2, ¹⁄_√2).

  2. Letting x,y,z be the side-lengths of the rectangular bin missing the top and front, the volume is g(x,y,z) = xyz = 1, with ∇g(x,y,z) = (yz, xz, xy). The surface area of the four sides is f(x,y,z) = xy + yz + 2xz, with ∇f(x,y,z) = (y+2z, x+z, y+2x). The Lagrange Multiplier method gives equations ∇f(x,y,z) = λ ∇g(x,y,z) and g(x,y,z) = 1, solved for variables x,y,z > 0, and λ:

  y + 2z = λyz,   x + z = λxz,   y + 2x = λxy,   xyz = 1.
  Note that these equations are symmetric in x and z. If λ = 0, we get x = y = z = 0, which is excluded. Since x,y,z,λ ≠ 0, we can divide the first two equations to get ^{y + 2z}⁄_{x + z}  =  ^yz⁄_xz , and cross-multiplying implies 2x = y. Similarly 2z = y, so the last equation gives ^y3⁄₄ = 1, and (x,y,z) = (2^−1/3, 2^2/3, 2^−1/3), agreeing with the method in our previous HW.

• ⊞ 2/26: Lect 20. Midterm Review 
  See the Weekly HW due 3/3 below.
  The Midterm will cover all the material so far, as in the Notes, HW, and especially the Quizzes.
  HW:

  1. Vector algebra. Consider the plane P containing (endpoints of) the vectors a = (0,1,1), b = (1,1,0), c = (2,2,2).
     1. Find a parametric equation p(s,t) = (x(s,t), y(s,t), z(s,t)) for the points of P.
     2. Find an equation for P as a level surface: ax + by + cz = d. (You will need a normal direction vector n, orthogonal to the directions along the plane.)
     3. Find the area of the triangle △abc, which is half the area of an appropriate spatial parallelogram.
     4. Find the distance from the origin to the plane P. (Project a vector on the plane to the normal direction n.)
     5. Find the volume of the tetrahedron with vertices 0,a,b,c as ¹⁄₃ the area of the base triangle in part (c), times the height from part (d).
     6. Find the above tetrahedron volume another way, as ¹⁄₆ the volume of the parallelopiped spanned by edges a,b,c.
  2. Line integrals. Consider the vector field F(x,y) = (2x, 1).
     1. Sketch the field F, plotting sample vectors at grid points.
     2. Does it look like F is the gradient field (uphill vectors) of a potential function, i.e. F = ∇f? Sketch the contour lines and graph of this hypothetical f(x,y).
     3. Review the argument that F has a potential function if and only if it has zero curl everywhere.
        • Gradient Theorem:   F = ∇f  ⇒  f(c(1)) = f(c(0)) + ∮F(c)•dc is path independent (depends only on endpoints).
        • ∮F path independent  ⇔  F irrotational (∮F = 0 on any closed path)
        • Curl Theorem (Green-Stokes Theorem):  F irrotational  ⇔  curl F = 0 everywhere.
     4. Recall the pictorial meaning of curl F, why curl(0,x) = 1, curl(y,0) = −1, and curl(p,q) = ^∂q⁄_∂x − ^∂p⁄_∂y .
     5. Compute curl F.
     6. Compute f(a,b)  =  ∮ F(c)•dc  =  ∫¹₀ F(c(t))•c'(t) dt for the straight line c(t) = (ta,tb) from (0,0) to (a,b). Compare to (b) above.
  3. Linear mappings and matrices
     1. Let ℓ₀ : R² → R² be the ¹⁄₄ counterclockwise rotation. Write its 2×2 matrix [ ℓ₀ ]  =  [ ℓ₀(i) | ℓ₀(j) ].
     2. In R³, compute the 3×3 matrix of a ¹⁄₄ rotation ℓ_z around the z-axis, and similarly ℓ_x around the x-axis.
     3. Multiply matrices to calculate the composite mapping: [ℓ_z∘ ℓ_x]  =  [ ℓ_z ] • [ ℓ_x ].
     4. Picture ℓ_z∘ ℓ_x by its effect on the unit vectors i, j, k, and describe it as a rotation.
  4. Consider the mapping f : R² → R³ defined by f(v) = (|v|, |v−i|, |v−j|), recording the distances from v to the origin and the two coordinate vectors.
     1. Find the Jacobian matrix of f at c = (½, 0), and write the affine linear approximation for f(x,y) near this point.
     2. Explain the form of the Jacobian geometrically: how could you have approximately predicted [ Df(c) ] without computing?
     3. For g(x,y,z) = x+y+z, use the Chain Rule compute the Jacobian matrix of g∘f, and check that ∇(g∘f)(v) = ^v⁄_|v| + ^v−i⁄_|v−i| + ^v−j⁄_|v−j|.
        Extra Credit: Show the sum of distances g(f(v)) is minimized when the three vectors v, v−i, v−j are all 120° from each other.
  ⊞ Solutions

  1a. Subtracting any two points on the plane P gives a direction along (parallel to) the plane, for example c− a = (2,1,1) and c− b = (1,1,2). To get to any point on the plane, move in these two directions from a base point c:

  p(s,t)  =  (2,2,2) + s (2,1,1) + t (1,1,2)  =  (2+2s+t, 2+s+t, 2+s+2t).

  1b. A cross product u×w has direction orthogonal to u and w, and length |u| |w| sin θ_uw. Thus, we get a normal vector, orthogonal to P, as: n = (2,1,1) × (1,1,2) = (1,−3,1).
  Now, for any point v = (x,y,z) on P, the direction from c to v is orthogonal to n:

  (v−c) • n = 0   ⇔   v • n = c • n   ⇔   x−3y+z = 2

  1c. The area of a triangle with side lengths u,w enclosing angle θ is ½uw sin θ. Our triangle has side vectors u = c−a and w = c−b, so the area is half the length of the cross product n = u×w from in part (b): area(△abc) = ½|n| = |(1,−3,1)| = ½√11.

  1d. To get a vector m from the origin directly to the plane P, take any vector from the origin to P, such as c, and project it to the normal direction n orthogonal to P. The length of this projection is c dotted with the unit normal vector ⁿ⁄_|n|:

  |m|  =  | c • ⁿ⁄_|n| |  =  ^|c•n|⁄_|n|  =  ²⁄_√11

  1e. We can think of the tetrahedron as a cone (or pyramid) whose base is △abc and whose altitude is the vector m. The volume of any cone is ⅓ the base area times the height, which we know from parts (c) and (d), so the volume of our tetrahedron is: ¹⁄₃(^√11⁄₂)(²⁄_√11) = ¹⁄₃ .

  1f. The signed volume of the parallelpiped with edge vectors a, b, c is the determinant of the matrix of these three vectors (written as columns or rows: det(0,1,1; 1,1,0; 2,2,2) = −2, so the absolute volume is 2. The volume of a tetrahedron is ¹⁄₆ of this, namely ¹⁄₃ as before.

  2a. The vector F(x,y) = (2x,1) depends only on x, and gives the same vector everywhere on a vertical line y = c: a vector pointing upward and away from the y-axis. Wolfram Alpha gives:

  2b. F looks like the gradient field of a function which slopes upward along the y-axis, and gets steeper away from the y-axis. The contour curves f(x,y) = c cut orthogonally to the vectors of F: Lifting these contours to their proper heights makes the graph z = f(x,y): 2c. We recall why F having a potential function is equivalent to curl F = 0.

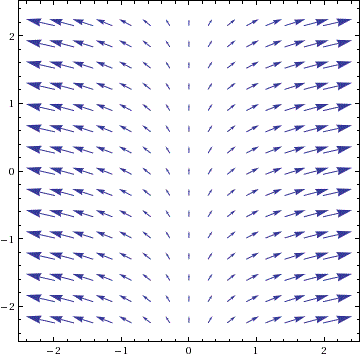
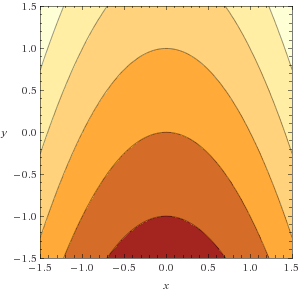
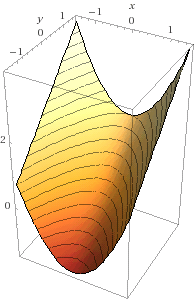
  First step. Assume F = ∇f for some potential function f. Gradient Theorem: The line integral of the rate of increase of f along a curve is the total increase along the curve: ∮ ∇f(c) • dc = f(c(1)) − f(c(0)). We can then compute f(a,b) by taking the line integral of ∇f(x,y) from a base point (0,0) to (a,b). This line integral depends only on the endpoints (0,0) and (a,b), and is independent of how c(t) travels between them.

  Second step. Suppose F is path indepenent. Given two paths c₁, c₂ between two points, we can follow the first path out and the second one back to get a closed curve c. Since the line integrals along c₁ and c₂ are equal, their difference, the line integral around c, is zero. That is, the vector field is irrotational, having zero line integral around any closed curve.

  Third step. Curl Theorem: The double integral of the rate of rotation of F over a region R is equal to the total rotation of F around the boundary of R. If F is irrotational, having zero total rotation around any closed curve, this means the rate of rotation at every point must be zero: curl F(x,y) = 0 everywhere.

  2d. See HW 1/20 #1. For F(x,y) = (p(x,y), q(x,y)), the curl F(x,y) = ^∂q⁄_∂x − ^∂p⁄_∂y measures how strongly a small paddlewheel at (x,y) would be turned by a fluid flowing with velocity F. A left-to-right increase in the vertical component of F leads to a positive (couterclockwise) curl, hence the term ^∂q⁄_∂x; a bottom-to-top increase in the horizontal component of F leads to a negative (clockwise) curl, hence the term −^∂p⁄_∂y.

  2e. curl F = ^∂⁄_∂x(1) − ^∂⁄_∂y(2x) = 0. Thus F is irrotational, and must have a potential function f.

  2f. We compute the potential function f(x,y) at (x,y) = (a,b) as the line integral of F(x,y) = (2x, 1) along the straight-line path c(t) = (at, bt) for 0 ≤ t ≤ 1:

  f(a,b)   =   ∮ F(c) • dc   =   ∮ F(c(t)) • c'(t) dt

    =   ∮₀¹ F(at, bt) • (at, bt)' dt   =   ∫₀¹ (2at,1) • (a,b) dt   =   ∫₀¹ 2a²t + b dt   =   a² + b.

  
  Thus, f(x,y) = x² + y, and we can verify that ∇f = F.

  3a. The quarter-turn ℓ₀ takes i to j = (0,1), and j to −i = (−1,0). The corresponding matrix of column-vectors is:

  [ ℓ0 ]   =     0   −1  1  0

  3b. The z-axis quarter-rotation takes i to j, j to −i, and k to itself. These output vectors are the column vectors of the matrix; and similarly for the x-axis quarter-rotation. (Note: we are using the right-handed rotation, in which the thumb points along the positive axis of rotation, and the fingers curl in the rotation direction.)

  [ ℓz ]   =     0   −1     0   1 0 0 0 0 1

  [ ℓx ]   =     1     0   0 0 0 −1   0 1 0

  3c. Multiplying the above gives the matrix of composite linear mapping ℓ_z(ℓ_x(v)):

  [ ℓz ∘ ℓx ]   =     0     0     1   1 0 0 0 1 0

  3d. The columns of the above matrix are the outputs of the coordinate vectors: the mapping takes i → j → k → i. That is, the equilateral triangle with corners at i,j,k is rotated around its center ⅓(i+j+k) = (⅓,⅓,⅓). This means the linear mapping is a 120° rotation around the axis (⅓,⅓,⅓), or equivalently the axis (1,1,1). Note that composing in the other order, ℓ_x ∘ ℓ_z, gives a 120° rotation around a different axis.

  4a. The Jacobian at (x,y) = (½, 0) of:

  f(x,y) = ( (x²+y²)^1/2, ((x−1)²+y²)^1/2, (x²+(y−1)²)^1/2 )
  is:

  [ Df(½, 0) ]   =    x⁄(x2+y2)1/2  y⁄(x2+y2)1/2  (x−1)⁄((x−1)2+y2)1/2  y⁄((x−1)2+y2)1/2  x⁄(x2+(y−1)2)1/2  (y−1)⁄(x2+(y−1)2)1/2

  =

  1      0  −1  0 1⁄√3 −2⁄√3

  4b. The point (x,y) = (½, 0) is on the line between 0 and i. We can predict the first column of the Jacobian by seeing that moving along the x-axis will have exactly opposite effects on the distances to 0 and i, which accounts for the +1 and −1; while it increases the distance to j at a positive rate, accounting for the bottom entry. As for the second column, moving vertically will affect the distances to 0 and i only tangentially (quadratically), so the first two rows are zero; while the last row is negative, since the vertical motion decreases the distance to j.

  4c. The derivative of g(x,y,z) = x+y+z is the row-vector gradient: ∇g(x,y,z) = [1   1   1]. Multiplying a 1×3 matrix by a 3×2 matrix gives a 1×2 matrix, whch is the gradient of g(f(x,y)).

• ⊞ 3/14: Lect 21. 4 Curves, arclength, vector fields, div, curl, acceleration, Newton's 2^nd Law.
  Reading: M&T pp. 217−255.
  HW:

  1. Div and curl for three dimensions.
     1. Defining the symbolic vector ∇ = (^∂⁄_∂x , ^∂⁄_∂y , ^∂⁄_∂z), explain why we may write div F = ∇ • F and curl F = ∇ × F as a device for remembering the formulas for div and curl.
     2. If a three-dimensional vector field is a lifting of a two-dimensional one, with formula F(x,y,z) = (F₁(x,y), F₂(x,y), 0), explain how the three-dimensional curl F relates to the two-dimensional curl (F₁, F₂). What is the axis of rotation?
  2. Consider a general radial vector field F : R³ → R³ given by F(v) = g(r) v, where g(r) is a scalar function of the radius r = |v| = √(x² + y² + z²).
     1. Compute the divergence div F(x,y,z), in terms of the derivative g'(r). Hint: Write out F(x,y,z), take the partial derivatives, and add.
     2. Compute the divergence for the unit-length radial vector field F(v) = ¹⁄_r v. Explain why the net outflow of F from a polar-coordinate box is positive, even though the vectors have constant length.
     3. Prove that div F = 0 everywhere if and only if g(r) = ^c⁄_r³ for c a constant, so that |F(v)| is proportional to the inverse-square radius ¹⁄_r² .
     4. Prove that any radial vector field has curl F = (0,0,0) everywhere.
  3. Prove that div curl F = 0 everywhere, for any three-dimensional vector field F.
  4. Suppose a particle moves along a circular orbit of radius R around the origin, given by the formula: c(t)  =  ( R cos(^S⁄_R t), R sin(^S⁄_R t) ), where S is a constant.
     1. Show that the particle is moving with constant speed S.
     2. Now suppose the particle is moving in an inverse-square force field F(v) = ^a⁄_r³ v, and obeying Newton's 2^nd Law:  F(c(t)) = m c''(t). Show that the orbital speed must be inversely proportional to the square root of the radius: S = ^b⁄_√R for a constant b independent of R and S.
     3. Prove Kepler's Third Law of Planetary Orbits: the square of the period (the time for one full orbit) is proportional to the cube of the radius.
  5. Find the arclength of one turn of the helix (screw curve) c(t) = (cos(t), sin(t), t).
  ⊞ Solutions

  1a. Considering a derivative operator like ^∂⁄_∂x as a "scalar", we can "multiply" it by a scalar function f(x,y,z) to give the partial derivative ^∂⁄_∂x f(x,y,z). Then taking the dot product of the "vector" ∇ = (^∂⁄_∂x , ^∂⁄_∂y , ^∂⁄_∂z) with a vector field F = (F₁, F₂, F₃) gives the formula for the divergence:

  ∇ • F  =  ^∂⁄_∂x F₁ + ^∂⁄_∂y F₂ + ^∂⁄_∂z F₃  =  div F.
  We can similarly compute the cross product ∇ × F = curl F.

  1b. We have curl F = curl (F₁(x,y), F₂(x,y), 0) = (0, 0, ^∂⁄_∂x F₂ − ^∂⁄_∂y F₁) = (curl (F₁, F₂)) k. That is, the axis of rotation is vertical, and the strength of the rotation at (x,y,z) is the same as the strength of the two-dimensional vector field at (x,y).

  2a. We can compute divergence this by taking partial derivatives of each component in:

  F(x,y,z) = ( g(√(x²+y²+z²)) x , g(√(x²+y²+z²)) y , g(√(x²+y²+z²)) z).
  Alternatively, we can use a product rule for the divergence of f F, the scalar multiple of F : R³ → R³ by f : R³ → R;

  div(f F)  =  ∇ • (f F)  =  ∇f • F + f ∇ • F .
  This is easy to verify (see p. 255 #7). Then for v = (x,y,z) and r = √(x²+y²+z²), we have:

  div F  =  ∇ • (g(r) v)  =  ∇(g(r)) • v + g(r) ∇ • v
   =  g'(r) ∇(r) • v + g(r) ∇ • v  =  g'(r) ^v⁄_r • v + 3 g(r)  =  r g'(r) + 3 g(r).
  2b. We have: div ¹⁄_r v  =  − ^r⁄_r² + ³⁄_r  =  ²⁄_r . A polar coordinate box has an inflow of F across its short inner edge (a circular arc), an outflow of F across its long outer edge, and no flow across its radial side edges. Thus, we clearly should have a positive net outflow, and hence positive divergence.

  2c. To find when div g(r) v  =  r g'(r) + 3 g(r)  =  0, we must solve the separable differential equation: r ^dg⁄_dr  =  −3g. That is, ∫ ^dg⁄_g  =  −3 ∫ ^dr⁄_r , which means log(g) = −3 log(r) + C, so that g(r) = exp(−3 log(r) + C)  =  ^c⁄_r³ . Thus F(v) = ^c⁄_r³ v, a radial vector field with magnitude proportional to the inverse-square of the radius.

  2d. As in part (a), we can compute component by component, or use p. 255 #10 to get:

  curl F  =  ∇ × (g(r) v)  =  ∇(g(r)) × v + g(r) ∇ × v  =  g'(r) ^v⁄_r × v + g(r) ∇ × v  =  0,
  since v × v = 0 and ∇ × v = (^∂⁄_∂x , ^∂⁄_∂y , ^∂⁄_∂z) × (x,y,z) = 0.

  3. The formula div curl F = ∇ • (∇ × F) = 0 follows from the same algebra that proves u • (u × v) = 0 for any vectors u, v ∈ R³. You can check it by brute-force computation.

  4. See p. 220−221.

  5. The arclength is: ∫ |c'(t)| dt = ∫₀^2π √(x'(t)²+ y'(t)²+z'(t)²) dt = ∫₀^2π √(sin²(t)+ cos²(t)+1) dt = 2π√2.

• ⊞ 3/17: Recitation problems: vector fields, div and curl.
  HW: For each vector field below, I have drawn its flow lines (curves following the arrows). For each field:

  1. From the picture, estimate the div and curl of the field.
  2. Give a vector field formula which approximates the given flow lines.
  3. Compute the div and curl of your formula, and compare with your prediction.

  The flow line pictures are:

  1. Two roughly vertical streams along the positive and negaitve z-axis; as they approach the xy-plane, they flatten out until they become roughly horizontal.
  2. A tornado with helical or spiral-helical flow lines around the z-axis.

• ⊞ 3/16−18: Lect 24−25. 5 Double and triple integrals.
  HW:

  1. Let F : R³ → R³ be a differentiable vector field, and f : R³ → R a scalar function. Compute and simplify the following second derivatives.
     1. curl grad f = ∇ × (∇f)
     2. div curl F = ∇ • (∇ × F)
     3. div grad f = ∇ • (∇f). This is called the Laplacian of f, usually denoted ∇²f.
  2. (p. 270 #7) A vertical cylinder of radius r (representing a tree trunk) has a wedge W lying above the xy-plane and below the plane through the y-axis at angle θ from horizontal.
     1. Find the volume of the wedge as the double integral ∬ f(x,y) dA. Interpret the inner integral as an area. Hint: Compute the integral in the most advantageous order, dA = dy dx or dx dy.
     2. Write the above volume a triple integral ∫∫∫ dz dy dx, specifying W as the points (x,y,z) with a₁ ≤ x ≤ a₂,   b₁(x) ≤ y ≤ b₂(x),   c₁(x,y) ≤ z ≤ c₂(x,y).
     3. Write the above triple integral in five other ways corresponding to dV = dz dx dy = dy dz dx = dy dx dz = dx dz dy = dx dy dz.
  3. In class, we proved Fubini's Theorem using the Integral Mean Value Theorem: The average of a continuous function over an interval is equal to some value of the function inside the interval:
     ¹⁄_(b−a) ∫^b_a f(x) dx  =  f(c)   for some c ∈ (a,b).
     Prove this from the usual Mean Value Theorem for the derivative of the function F(x) = ∫^x_a f(t) dt.
  4. Consider the circular cylinder C₁ consisting of the points within distance 1 from the x-axis; and similarly C₂ for the y-axis. Now define the solid S = C₁ ∩ C₂, the region inside both cylinders.
     
     
     1. Give equations for the two cylinders, and describe S by inequalities of the form:
        a₁ ≤ z ≤ a₂
        b₁(z) ≤ y ≤ b₂(z)
        c₁(z,y) ≤ x ≤ c₂(z,y)
        Hint: The xy-shadow of S is the largest horizontal cross-section. Find the level z = c of this cross-section, and plug z = c into the equations.
     2. Find the volume of S by evaluating a triple integral.
  5. Define the solid S as the region above the surface z = x² − 2 and under z = 2 − y².
     
     
     1. Describe the boundary curve where the two surfaces meet, first by equations in x,y,z; then give it as a parametrized curve c(t).
     2. Find the most coordinate convenient plane where we can project the solid S, and describe its shadow. Set up and evaluate the triple integral giving the volume of S.
  ⊞ Solutions

  1. See the identities on p. 255.

  1a. curl grad f = (0,0,0) for any function, which you can check from the definitions, coordinate-by-coordinate.

  1b. div curl F = 0.

  1c. div grad f = ^∂2f⁄_∂x² + ^∂2f⁄_∂y² + ^∂2f⁄_∂z² .

  2a. See picture on p. 270 #7. The wedge is defined by x² + y² ≤ r and 0 ≤ z ≤ mx, where m = tan θ. Writing the xy-shadow in y-simple form: -r ≤ x ≤ r,   √−(r²−x²) ≤ y ≤ (r²−x²); and also 0 ≤ z ≤ mx. The volume integral becomes:

  ∫^r₀ ∫^√(r2−x2) _{−√(r²−x²)}  mx dy dx  =  ²⁄₃ mr³.

  The inner integral is the area of the rectangular vertical cross-section of the solid in the plane y = c, where c is a fixed value of x.

  3. See notes on More Integral Applications, last page, from Math 132.

• ⊞ 3/21: Lect 26. 6.3 Applications of Integrals.
  See the Weekly HW due 3/25 below.
  HW:

  1. Represent a wire curving through the plane by a parametrized curve C = c(t) = (x(t), y(t)) for t₀ ≤ t ≤ t₁, with density function δ(t), given for example in grams per centimeter. Give a formula for the x- and y-coordinates of the center of gravity of C, in terms of a line integral over C. Hint: Find the average of x(t) and of y(t), wieghted by the density.
  2. Consider a triangular plate T in the plane with uniform density, and with corners (0,0), (a, 0), (b₁, b₂), where a,b₂ > 0.
     1. Find the center of gravity if the weight is concentrated in uniform amounts at the three corners.
     2. Find the center of gravity if the weight is uniformly distributed over the area of the plate.
     3. Find the center of gravity, assuming the weight is uniformly concentrated on the boundary lines of the triangle.
  ⊞ Solutions

  1. Repeating the definition of center of gravity as the average value of each coordinate x,y, weighted by mass = density × length along the curve c(t), we get:

  x  =  ¹⁄_L ∮ x(t) δ(t) |dc|  =  ¹⁄_L ∫ x(t) δ(t) |c'(t)| dt,
  y  =  ¹⁄_L ∮ y(t) δ(t) |dc|  =  ¹⁄_L ∫ y(t) δ(t) |c'(t)| dt,

  where L = ∫ δ(t) |c'(t)| dt is the arclength.

  2a. The center of gravity of the three corners is the average of their vectors: ⅓((0,0) + (a, 0) + (b₁, b₂)) = (⅓a + ⅓b₁, ⅓b₂).

  2b. The triangular region is bounded by lines y = 0,   y = ^b₂⁄_b1 x,   y = ^b₂⁄_(b1−a) (x−a). This can be split into two adjacent y-simple triangles corresponding to the two different floor-lines (for b₁ > a) or ceiling-lines (for b₁ < a). However, since one side of the triangle is the x-axis, the whole triangle is an x-simple region: 0 ≤ y ≤ b₂, ^b₁⁄_b2 y ≤ x ≤ ^(b₁−a)⁄_b2 y + a. The double integrals ¹⁄_A (∬_R x dA, ∬_R y dA), where the area is A = ½ab₂, give the same answer as in part (a).

  2c. Splitting the line integral over the three line segments gives:

  (x, y) = ^{½(a|a| + b|b| + (a+b)|a−b|)} ⁄ _{(|a| + |b| + |a−b|),}

  which is definitely different from parts (a), (b).

• ⊞ 3/23−3/25: Lect 27−28. 6.2 Change of variable formula.
  See the Weekly HW due 3/25.
  HW:

  1. Gaussian integral   I = ∫ _−∞ ^∞ e^−x2 dx. The integrand e^−x2 is the or bell-curve or normal distribution which gives the relative probability of a random variable x, assuming x has expectation value zero. (For example, x could be the height of a randomly chosen woman.)
     To make this a true probability distribution, we must scale it so that the total probability (the integral) is equal to one. That is, we must divide by the value of the integral I, but this is difficult to compute since e^−x2 has no elementary anti-derivative. We outline an amazing solution using double integrals and change of coordinates.
     1. Compute the double integral of e^−(x2+y2) over the disk x² + y² ≤ R², for a fixed radius R, and find the limit as R → ∞. Use polar coordinates.
     2. Show that the integral of e^−(x2+y2) over the rectangle [−R,R]×[−R,R] is equal to ( ∫ _−R ^R e^−x2)² dx.
     3. Compare the integral in (a) with that in (b), letting R → ∞, and compute the original integral I.
  2. Spherical coordinates
     1. Compute a Jacobian determinant to show that the volume form for spherical coordinates is: dx dy dz = ρ² sin(φ) dρ dθ dφ. (I miswrote this formula in class.)
     2. Re-do our example from class, finding the center of gravity of the solid inside the unit sphere x² + y² ≤ 1 and the cone x² + y² ≤ z², z ≥ 0.
  3. p. 348 #15: Use an appropriate change of variables to compute the integral ∬_B exp(^(y−x)⁄_(y+x)) dx dy over the triangle B with vertices (0,0), (1,0), (0,1).
     1. Consider the change of variables transformation (s,t) = T(x,y) = (y−x, y+x). Find its matrix [T], and verify that:

        s t

        =  [T] •

        x y

     2. Find the image region B* = T(B): this is a triangle with vertices T(0,0), T(1,0), T(0,1).
     3. Given (s,t) = (y−x, y+x), solve the two linear equations to get x,y in terms of s,t. Use this to write the inverse transformation U = T⁻¹ with (x,y) = U(s,t). Write the matrix [U] and verify that [U]•[T] = I, the identity matrix. Also B = U(B*).
     4. Write the Change of Variables formula for our integral, transforming it by U to (s,t) variables over B*.
     5. Evaluate the integral.
  4. Routine practice from M&T.
     1. p. 304 #15(a,b). Do with rectangular coordinates, then again with polar.
     2. p. 305 #25. Do with rectangular coordinates, then again with coordinates (s,t) defined by (x,y) = s (1,0) + t (2,1).
     3. p. 305 #27, 37.
  5. Review of vector fields, grad, div, curl. Consider the vector field F = (−y, x, 0) and a scalar function of the form f(x,y,z) = f(z) depending only on z.
     1. Describe F in words and sketch, and make a guess at its divergence and curl, based on their geometric meanings.
     2. Do the same for the product f F, that is, the vector field G(x,y,z) = f(z) F(x,y,z).
     3. Compute div F and curl F and compare with your guesses. Also compute grad f = ∇ f.
     4. Write the general product formulas for curl f F and div f F, and apply them to our case.
  ⊞ Solutions

  1. See M&T p. 332.

  2a. See p. 325.

  2b. S has an edge-curve with z² = r², and r² + z² = 1, hence r = z = ¹⁄_√2. Thus S is defined by: −¹⁄_√2 ≤ x ≤ ¹⁄_√2,   −√(¹⁄₂−x²) ≤ y ≤ √(¹⁄₂−x²),   √(x²+y²) ≤ z ≤ √(1−x²−y²). Under spherical coordinates, this pulls back to the box S* defined by 0 ≤ ρ ≤ 1,  0 ≤ θ ≤ 2π,  0 ≤ φ ≤ ^π⁄₄. Hence the volume is:

  V  =  ∭_S dz dy dx  =  ∭_S* ρ² sin(φ) dρ dθ dφ
   =  (∫₀¹ ρ² dρ) (∫₀^2π dθ) (∫₀^π⁄₄ sin(φ) dφ)  =  (¹⁄₃)(2π)(1−¹⁄_√2)  =  ^π⁄₃(1−¹⁄_√2).
  Because of symmetry, the center of gravity must have x = y = 0, and:

  z  =  ¹⁄_V ∭_S z dz dy dx  =  ¹⁄_V ∭_S* ρ cos(φ) ρ² sin(φ) dρ dθ dφ
   =  ¹⁄_V (∫₀¹ ρ³ dρ) (∫₀^2π dθ) (∫₀^π⁄₄ cos(φ)sin(φ) dφ)
   =  ¹⁄_V (¹⁄₄)(2π)(¹⁄₄)  =  ³⁄₁₆ (2+√2)  ≈  0.64 .
  This somewhat above the middle of the cone, which is reasonable.

  3a.   [T]  =

  −1  1    1 1

  3b. B* is the triangle with vertices (s,t) = (0,0), (−1,1), (1,1), given by 0 ≤ t ≤ 1,  −t ≤ s ≤ t.

  3c. (x,y) = (−½s + ½t , ½s + ½t).   [U]  =  [T]−1  =

  −½  ½    ½ ½

  
  

  This is indeed the inverse of [T], since:   [U] • [T]  =

  −½  ½    ½ ½

  •

  −1  1    1 1

  =

  1   0  0 1

  .

  3d,e. We have U(B*) = B, one-to-one and onto. Since U is linear, it is its own derivative at every point: DU_(s,t) = U, and |^∂(x,y)⁄_∂(s,t)| = det[U] = ½ . Also y−x = s, y+x = t. Thus:

  ∬_B exp(^(y−x)⁄_(y+x)) dx dy  =  ∬_B* exp(^s⁄_t)  |^∂(x,y)⁄_∂(s,t)| ds dt  =  ¹⁄₂ ∫⁰₁ ∫^t_−t e^s/t ds dt
   =  ¹⁄₂ ∫⁰₁ ∫^t_−t e^s/t ds dt  =  ¹⁄₄ (e−e⁻¹).
  4. See pp. 519−520

  5a. F = (−y, x, 1) is the velocity field of a right-handed rotation of space around the z-axis (i.e. right thumb along the z-axis, fingers curling toward the rotation). The velocity grows in proportion to the xy-radius.
  The divergence is the net outflow from a small region around a given point, per unit volume enclosed. Taking the region to be a small cylindrical-coordinate box, the inflow on one side equals the outflow on the other, and div F = 0.
  The curl is the right-handed axis of the rotation induced on a small paddlewheel floating in the flow of F near a given point, with magnitude equal to the force of rotation. This is clearly along the z-direction, with positive magnitude.

  5b. The product f F = f(z)(−y, x, 0) scales the speed of rotation for each horizontal plane. Thus, if f(z) = z, we could picture f F as a tornado, rotating slowly close to the ground, and faster and faster high up. (Below the xy-plane, the rotation would be reversed.) This would still have zero divergence, but the curl would be complicated by the shearing forces between horizontal layers, which depend on ^∂f⁄_∂z.

  5c.

  div F   =   ∇ • F   =   ^∂⁄_∂x(−y) + ^∂⁄_∂y(x) + ^∂⁄_∂z(0)   =   0.

  curl F   =   ∇ × F   =   det

  i	j	k
  ∂⁄∂x	∂⁄∂y	∂⁄∂z
  −y	x	0

    =   2k   =   (0,0,2).

  These are what we guessed.

  5d. Any product formula is of the form:  Δ(f∗g)  =  (Δf)∗g + f∗(Δg),  where each Δ is some type of derivative and each ∗ some type of product. In our cases, there is only one type of derivative and one type of product which will make sense at each place in the formula, keeping in mind that: gradient takes a scalar function to a vector field, div takes a vector field to a scalar function, and curl takes a vector field to a vector field:

  div f F   =   ∇ • (f F)   =   ∇f • F  +  (f) ∇•F
    =   (0, 0, ^∂f⁄_∂z) • (−y, x, 0)  +  f(z) 0   =   0.

  curl f F   =   ∇ × (f F)   =   ∇f × F  +  (f) ∇×F
    =   (0, 0, ^∂f⁄_∂z) × (−y, x, 0)  +  f(z) (0, 0, 2)   =   (−x ^∂f⁄_∂z , −y ^∂f⁄_∂z , 2 f(z)).

  Again, these are consistent with our guesses.

• ⊞ 4/1: Triple integrals exercise sheets.
  HW:

  • Triple integrals, especially #13, 19.
  • Spherical and cylindrical integrals, especially #10, 29.
  • Change of variables, especially #12.
  • Numerical answers  

  
  Ch 16-9. #12. Consider the region R bounded by the four circles:

  x² + y² = 2x,     x² + y² = 6x,     x² + y² = 2y,     x² + y² = 8y.
  This region is adapted to a coordinate system called the Apollonian or inversion coordinates, whose coordinate grid curves are circles centered on the x-axis or the y-axis, all of which pass through the origin. This is given by the inversion transformation:

  (x,y)  =  T(u,v)  =  (^2u⁄_(u²+v²) , ^2v⁄_(u²+v²)).
  This is a kind of "reflection" across the circle of radius √2 ; T takes a point (u,v) with radius r to a point (x,y) with the same polar angle and radius ²⁄_r. That is, T switches the inside and outside of the circle, with the origin going to infinity.

  1. Write the boundary circles of R in the form (x−a)² + (y−b)² = r² to show they are indeed Apollonian grid circles. (Hint: Complete the square.)
  2. Show that the line u = c in the (u,v)-plane corresponds to the circle (x−a)² + y² = a² in the (x,y)-plane, where a = ¹⁄_c; and similarly, the line v = c corresponds to the circle x² + (y−a)² = a². In the picture above, identify the blue circles as u = c and the red circles as v = c, for appropriate constants.
  3. Parametrize the region R as the points T(u,v) for a₁ ≤ u ≤ a₂ , b₁ ≤ v ≤ b₂ , for appropriate constants.
  4. Compute the Jacobian matrix [DT_(u,v)] and its determinant |det[DT_(u,v)]| = |^∂(x,y)⁄_∂(u,v)|, as it is written in the Change of Variables Formula.
  5. Use Change of Variables to rewrite the following integral in uv coordinates: ∬_R ¹⁄_(x²+y²)² dx dy.
  6. Verify that the inversion mapping T is its own inverse: that is, if (x,y) = T(u,v), then the variables u,v satisfy the equation (u,v) = T(x,y).

  ⊞ Solutions

  16-6 #13. The solid bounded by planes y + z = 4, y = 0, z = 0, and the parabolic cylinder y = 4−x².
  First examine the boundary surfaces involving only x,y: the back wall y = 0, and the curving front wall y = 4−x². Next consider the roughly horizontal surfaces involving z: the floor z = 0 and the slanted ceiling z = 4−x.

  This solid is clearly z-simple: a single floor and ceiling in the z-direction, above an xy-shadow contained between curves y = 0 and y = 4−x². Answer:   S = { (x,y,z) with −2 ≤ x ≤ 2,   0 ≤ y ≤ 4−x²,   0 ≤ z ≤ 4−x }. The volume is ¹²⁸⁄₅ .

  16-6 #19. The solid bounded by planes x + y + z = 2 and x = 0, and the parabolic cylinders y = z² and z = y².
  First examine the boundary surfaces involving only y,z: the parabolic cylinders cutting each other in a squashed cylinder. Next consider the surfaces involving x: x = 0 and x = 2 − y − z, which cut off the ends of the squashed cylinder.

  This solid is clearly x-simple: a single floor and ceiling in the x-direction, above a yz-shadow contained between the parabolas z = y² and y = z². Answer:   S = { (x,y,z) with 0 ≤ z ≤ 1,   √z ≤ y ≤ z²,   0 ≤ z ≤ 2 − y − z }. The volume is ¹¹⁄₃₀ .

  16-9 #12(a). The equation x² + y² = 2ax is equivalent to (x−a)² + y² = a², a circle centered at (a,0) with radius a, so that the circle contains the origin. The first two circles have centers (1,0) and (3,0), and similarly the second two have centers (0,1) and (0,4).

  12(b). The line u = c is parametrized by (c,t) for t ∈ R, which corresponds to (x,y) = T(c,t). It is easy to verify that x = ^2c⁄_(c²+t²) and y = ^2t⁄_(c²+t²) satisfy x² + y² = ²⁄_c x, which is equivalent to the circle equation. Similarly for v = c.

  

  12(c). From the picture, we see R = { (x,y) = T(u,v) for ¹⁄₃ ≤ u ≤ 1 , ¹⁄₄ ≤ v ≤ 1 }

  12(d). You can do this with Wolfram Alpha by pasting partial results into a scratch file, then pasting back into W|A. Result: the Jacobian determinant (streching factor) is |⁻⁴⁄_(u²+v²)²|  =  ⁴⁄_(u²+v²)² .

  12(e). The integral reduces to ∫¹_⅓ ∫¹_¼ (u²+v²)^{2 4}⁄_(u²+v²)² dv du  =  2.

  12(f). Use W|A to solve the system of equations x = ^2u⁄_(u²+v²) and y = ^2v⁄_(u²+v²) for the variables u,v. Keep in mind that the equations are symmetric upon switching u,v and simultaneously switching x,y, so a solution for u can be switched into a solution for v.
  Note: This is also evident from the polar description of T as an inversion across a circle of radius √2. Furthermore, we can write T as a conjugate inversion in the plane of complex numbers. That is, we let (x,y) correspond to the complex variable z = x + iy with conjugate z = x − iy; then T(x,y) corresponds to the mapping z ↦ ²⁄_z  =  ^2z⁄_zz.

• ⊞ 4/4−4/8: Lect 33−35. 7 Line & path integrals, parametric surface & flux integrals.
  Work out as much algbra as you can by hand, but for really complicated expressions, use a computer tool like Wolfram Alpha. (For complicated operations, save partial results as plaintext in a file, then copy into a new W|A page.) Here is a tool for parametric surface plots.
  HW:

  1. We consider a torus or donut surface with a core circle of radius R in the xy-plane, surrounded by vertical sectional circles of radius r ≤ R with centers on the core circle. We fix the core radius R and define the toric change of variables function
     T(r,θ,φ)   =   (x,y,z)

       =   R (cos(θ), sin(θ), 0)  +  r cos(φ) (cos(θ), sin(θ), 0)  +  (0, 0, r sin(φ)).

     If we fix the sectional radius r, we get a toric surface parametrized by: T(θ,φ)  =  T(r,θ,φ).
     1. Explain the geometric effect of each term in the formula for T.
     2. Find the 3×3 Jacobian derivative matrix:

        [DT]   =

        | ∂T⁄∂r | | ∂T⁄∂θ | | ∂T⁄∂φ |

        .

        
        Also, find the Jacobian determinant det[DT], which is the stretching factor |^∂(x,y,z)⁄_{|∂(r,θ,φ)}| in the Change of Variables Formula. This is best done by computer.
        Answer:  |^∂(x,y,z)⁄_{|∂(r,θ,φ)}|  =  r(R + r cos(φ)).
     3. Fix constant radius values r ≤ R, and compute the 2×3 Jacobian matrix [DT] = [ ^∂T⁄_∂θ | ^∂T⁄_∂φ ]. Its column vectors ^∂T⁄_∂θ , ^∂T⁄_∂φ span the tangent space of the torus at the point T(θ,φ). Also find the normal vector, the cross product n = ^∂T⁄_∂θ × ^∂T⁄_∂φ and its length |n|.
        Check your answer for (θ,φ) = (0,^π⁄₄), for which n should have slope 1 in the xz-plane.
        Hint: These are the same vectors you found in part (a) for T. Also, n = ^∂T⁄_∂r , so |n| is the same as the previous stretching factor.
     4. For the solid torus with given r ≤ R, use the Area Formula to find its surface area, and the Change of Variables Formula to find its volume.
        Answer:  Area = 4π²rR,  Volume = 2π²r²R .
  2. Explain the geometric effect of each term in the following parametric formula for the ram's horn surface:
     T(θ,φ)   =   20 (cos(θ), sin(θ), 0)  +  (0, 0, 10 θ)  +  θ cos(φ) (cos(θ), sin(θ), 0)  +  (0, 0, θ sin(φ)).
     
     
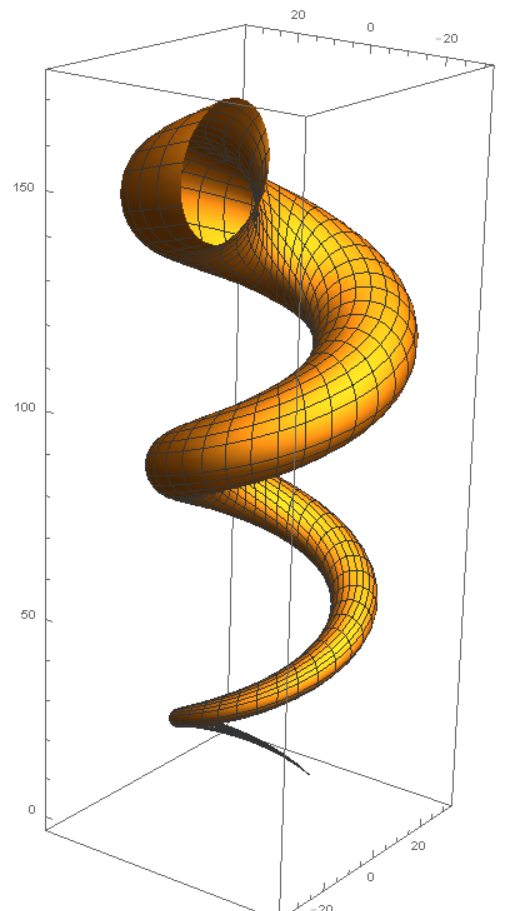
  3. Specialize the Area Formula to the following cases:
     1. Graph surface z = f(x,y). Hint: Parametrize by (x,y) coordinates.
     2. Surface of revolution z = g(√(x²+y²)). Hint: Parametrize by (r,θ) coordinates.
     3. Check your answer in (b) by applying it to the section of a right circular cone with height a and base radius b: this surface has equation z = ^a⁄_b √(x²+y²). We can unroll the surface to get a circular sector with radius √(a²+b²) and outer circumference 2πb, and we can find its area without calculus.
     Here f(x,y) and g(r) are arbitrary scalar functions. (These problems are from in Recitation 4/7.)
  4. Consider the helicoid surface S (M&T p 386) parametrized by: P(u,v) = (u cos(v), u sin(v), v) over the parameter rectangle S* = {(u,v) with 0 ≤ u ≤ 1, 0 ≤ v ≤ 2π}.
     1. Find the area A = ∬_S* |^∂P⁄_∂u × ^∂P⁄_∂v| du dv
     2. For a typical point such as P(1,0), sketch the tangent vectors ^∂P⁄_∂u , ^∂P⁄_∂v and use the right-hand rule to estimate the normal vector n = ^∂P⁄_∂u × ^∂P⁄_∂v: does n point up or down? What would be the normal vector corresponding to the switched parametrization Q(u,v) = P(v,u)?
     3. Sketch the vector field F(x,y,z) = (0,y,1) by plotting arrows in the yz-plane. Geometrically estimate the flux of F through the helicoid S: remember that this depends on the component of F parallel to n.
     4. Compute the flux integral ∬_S* F(P(u,v)) • (^∂P⁄_∂u × ^∂P⁄_∂v) du dv
  5. Work out for yourself some of the Examples in the book, before looking at the solutions. Especially:
     • 7.2 Ex 1, 2, 8, p 360.
     • 7.3 Ex 3, p 380.
     • 7.5 Ex 1, 2, 3, p 394.
     • 7.6 Ex 1, 4, p 401. Exercise 1, p 411.
  ⊞ Solutions

  1a. Consider the torus parametrization:

  T(r,θ,φ)   =   R (cos(θ), sin(θ), 0)  +  r cos(φ) (cos(θ), sin(θ), 0)  +  (0, 0, r sin(φ)). The first term parametrizes the core circle of radius R in the xy-plane by the angle θ, similar to the usual polar coordinate mapping. On a vertical circle of radius r, a radial vector tilted by angle φ from horizontal has horizontal component r cos(φ) and vertical component r sin(φ). This horizontal component should be in direction (cos(θ), sin(θ), 0), giving the second term, and the vertical component should be in direction (0, 0, 1), giving the third term.

  1b. The Jacobian derivative matrix is:

  [DT]   =

  cos(φ) cos(θ) cos(φ) sin(θ) sin(φ) −sin(θ)(r cos(φ)+R) cos(θ)(r cos(φ)+R) 0 −r sin(φ) cos(θ) −r sin(φ) sin(θ) r cos(φ)

  .

  
  The Jacobian determinant simplifies to: det[DT] = r(R + r cos(φ)).
  W|A can compute this if you input the above 3×3 matrix in the format {{a,b,c},{d,e,f},{g,h,i}}. The determinant remains the same if you transpose rows and columns.

  1c. The tangent vectors ^∂T⁄_∂θ , ^∂T⁄_∂φ of T(θ,φ) are the same as the corresponding derivatives of T(r,θ,φ): the last two columns of the Jacobian matrix in part (b). The normal vector is:

  n  =  ^∂T⁄_∂θ × ^∂T⁄_∂φ  =  r (R + r cos(φ))  (cos(φ) cos(θ), cos(φ) sin(θ), sin(φ)).
  This is a scalar times the unit vector (cos(φ) cos(θ), cos(φ) sin(θ), sin(φ)), which happens to be the same as ^∂T⁄_∂r : that is, the radial derivative vector of T is the unit orthogonal to the other two derivative vectors, which is evident from the geometry. Therefore the length of the cross product is the same as the determinant in part (b):  |n| = r (R + r cos(φ)).

  1d. The area of the torus is:

  A  =  ∫₀^2π∫₀^2π r (R + r cos(φ)) dφ dθ
   =  [2π r (Rφ + r sin(φ))]^2π_φ=0 = 4π²rR.
  We temporarily denote the fixed sectional radius by r₀, so that the solid torus has 0 ≤ r ≤ r₀. Then the volume is:

  V  =  ∫₀^r₀∫₀^2π∫₀^2π r (R + r cos(φ)) dφ dθ dr
   =  ∫₀^r₀ A(r) dr  =  ∫₀^r₀ 4π²rR dr  =  2π²r₀²R .
  The replacing r₀ with r, we get V = 2π²r²R .
  Note that A(r) = ^d⁄_drV(r). This is clear from the ∫ A(r) dr in the calculation, which comes about because of the unit orthogonality of the radial coordinate descibed in part (c). Geometrically, this means that an increment of Δr produces a layer of uniform thickness Δr over the toric surface, so that the rate of change of volume is the area.

  2. Ram's horn surface:

  T(θ,φ)   =   20 (cos(θ), sin(θ), 0)  +  (0, 0, 10 θ)  +  θ cos(φ) (cos(θ), sin(θ), 0)  +  (0, 0, θ sin(φ)).
  The first term produces a horizontal motion controlled by angle θ around a circle of radius 20; the second term produces a uniform upward motion along with the horizontal turning; and these two combine to trace a helix or corkscrew curve which is the core of the ram's horn. From this core, we move along a vertical sectional circle controlled by parameter φ, similarly to 1(a) above; but the radius of this sectional circle is equal to θ, becoming wider as we trace around the helix.

  3a. The graph z = f(x,y) is parametrized by T(x,y) = (x, y, f(x,y)), giving stretching factor:

  |^∂T⁄_∂x × ^∂T⁄_∂y|  =  |(1, 0, ^∂f⁄_∂x) × (0, 1, ^∂f⁄_∂y)|
   =  |(^−∂f⁄_∂x ,^−∂f⁄_∂y , 1)|  =  √(1 + (^∂f⁄_∂x)² + (^∂f⁄_∂y)²).
  The area is:

  A  =  ∬ √(1 + (^∂f⁄_∂x)² + (^∂f⁄_∂y)²) dx dy.
  This will usually be over some finite region (x,y) ∈ R* in the xy-plane.

  3b. The surface of revolution z = g(√(x²+y²) is parametrized by the cylindrical coordinate mapping T(r,θ) = (r cos(θ), r sin(θ), g(r)), giving stretching factor:

  |^∂T⁄_∂r × ^∂T⁄_∂θ|  =  |(cos(θ), sin(θ), g'(r)) × (−r sin(θ), r cos(θ), 0)|
   =  |r (cos(θ) g'(r) , sin(θ) g'(r) , 1)|  =  r √(1 + g'(r)²) .
  The area is:

  A  =  ∬ r √(1 + g'(r)²) dr dθ
  Again, this is over a parameter region (r, θ) ∈ R*.

  3c. The right circlular cone with height a and base radius b has a vertex-to-rim radius of ρ = √(a²+b²), and a rim circumference C = 2πb. We can unroll the lateral surface into a sector of a circle of radius ρ, with circular arc C. The area A of a sector is proportional to its circular arc, so ^C⁄_2πρ = ^A⁄_πρ² . That is: A = πb√(a²+b²).

  The cone is parametrized by T(r,θ) = (r cos(θ), r sin(θ), ^a⁄_b r) for 0 ≤ r ≤ b and 0 ≤ θ ≤ 2π. The formula of part (b) becomes:

  A  =  ∬ r √(1 + g'(r)²) dr dθ  =  ∫₀^2π ∫₀^b r √(1 + (^a⁄_b)²) dr dθ
   =  [ 2π√(1 + (^a⁄_b)²) ^r2⁄₂ ]_r=0^b  =  πb√(a²+b²).
  4a. For the area of the helicoid P(u,v) = (u cos(v), u sin(v), v) for 0 ≤ u ≤ 1 and 0 ≤ v ≤ 2π, see M&T p. 387. Answer: π(√2 + log(1+√2)) ≈ 7.2 .

  4b. For P(u,v) = (u cos(v), u sin(v), v) at (u,v) = (1,0), we have:

  ^∂P⁄_∂u = (cos(v), sin(v), 0) = (1,0,0)
  ^∂P⁄_∂v = (−u sin(v), u cos(v), 1) = (0, 1, 1).
  If I point my index finger along the first vector (radially along the x-axis) and my middle finger along the second vector (up the ramp in the y-direction), then my thumb points upward and back along the y-direction: n = (1,0,0) × (0,1,1) = (0,−1,1). Similarly, the normal vector at any point points upward.

  If we changed the parametrization to Q(u,v) = P(v,u), switching the roles of (u,v), we would get the opposite cross product ^∂Q⁄_∂u × ^∂Q⁄_∂v = (0,1,1) × (1,0,0) = (0,1,−1) pointing downward.

  4c. The vector field F(x,y,z) = (0,y,1) is independent of x, and is illustrated by its picture in the yz-plane:

  The vectors have length slightly larger than 1, and flow primarily upward and outward away from the xz-plane. The F vectors are rougly parallel to the normal vectors n of the helicoid, so the flux is positive; but the directions are not very close away from the yz-plane, so the flux is probably smaller than the area.

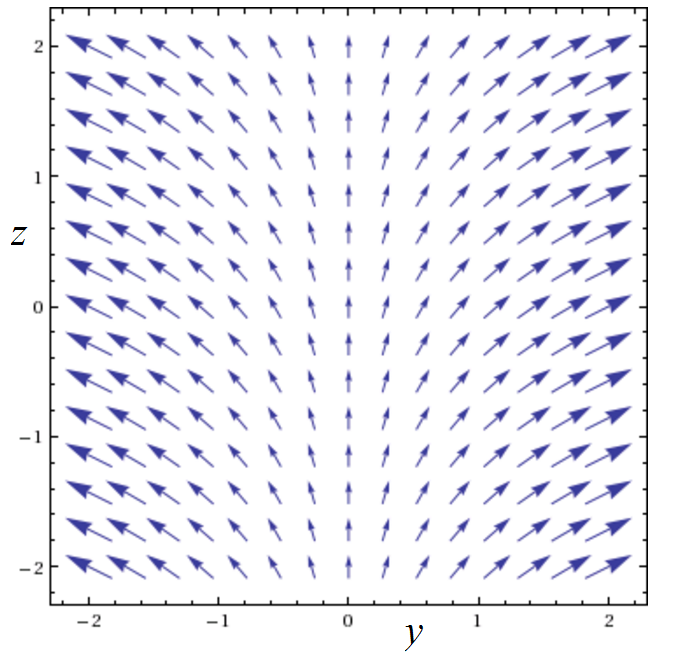
  4d. The flux integral is:

  ∬ F(P(u,v)) • (^∂P⁄_∂u × ^∂P⁄_∂v) du dv
   =  ∫₀^2π ∫₀¹ F(u cos(v), u sin(v), v) • ((cos(v), sin(v), 0) × (−u sin(v), u cos(v), 1)) du dv
   =  ∫₀^2π ∫₀¹ (0, u sin(v), 1) • (sin(v), −cos(v), u) du dv
   =  ∫₀^2π ∫₀¹ −u sin(v) cos(v) + u du dv  =  π  ≈  3.1 .

  This is consistent with our geometric estimate.

  5. Examples are worked out in the text. Answers for odd-numbered exercises are on p. 526.

• ⊞ 4/11−4/13: Lect 36−37. 8.1 Green's Theorem
  • Consider a vector field F in the plane R², a simple plane region R, and the curve c which is the counterclockwise boundary of R. (For more general R, possibly with holes, the boundary curves should be oriented so that the region is on the left as you traverse each curve.)
  • In coordinates, we write F(x,y) = (P(x,y), Q(x,y)) and c(t) = (x(t), y(t)). We can write a line integral as:
    ∮ F • dc  =  ∮_c (P dx + Q dy)  =  ∫ P(x(t), y(t)) x'(t) dt + ∫ Q(x(t), y(t)) y'(t) dt.
    
  • Curl Theorem (Green-Stokes Theorem): The integral of the rate of rotation over R is equal to the total rotation around the boundary of R:
    ∬_R curl(F) dy dx  =  ∮ F(c) • dc.
    In coordinates:   ∬_R (^∂Q⁄_∂x − ^∂P⁄_∂y) dy dx  =  ∮_c (P dx + Q dy).
    
  • Divergence Theorem (Green-Gauss Theorem): The integral of the rate of outflow over R is equal to the total net outflow across the boundary of R:
    ∬_R div(F) dy dx  =  ∮ F(c) • dn,
    where n is the outward-pointing normal to c, meaning dn = (−c')^⊥ dt = (y'(t), −x'(t)) dt.
    In coordinates: ∬_R (^∂P⁄_∂x + ^∂Q⁄_∂y) dy dx  =  ∮_c (P dy − Q dx).
  • The two coordinate equations are equivalent to each other. In the first equation, we replace F = (P, Q) by F^⊥ = (−Q, P) to obtain the second equation.

  HW:

  1. Go through our proof of the Curl Theorem for the specific case of the vector field F(x,y) = (x+1, xy) and the y-simple region R = {(x,y) with −1 ≤ x ≤ 1, 0 ≤ y ≤ 1+x²}.
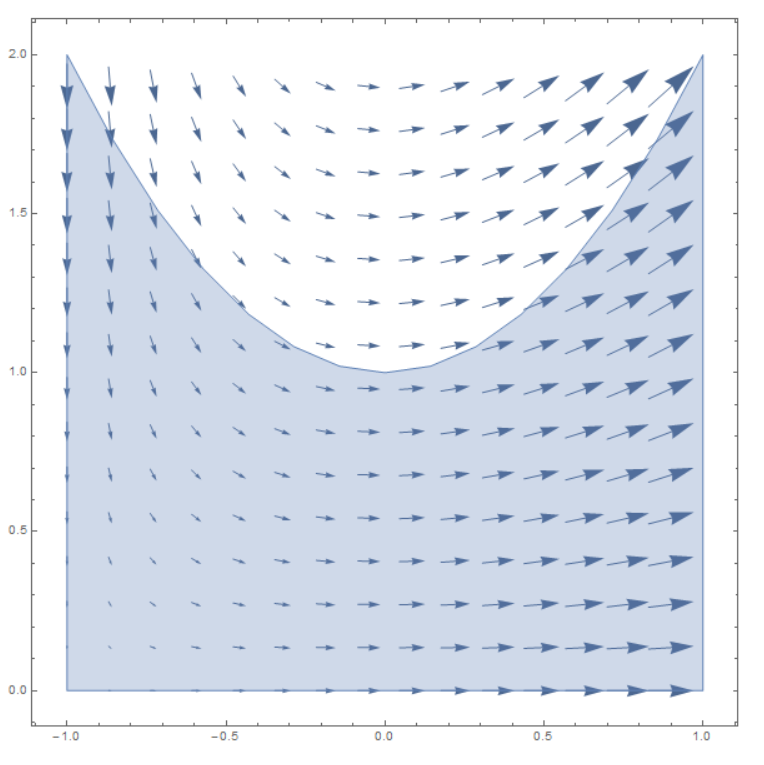
     1. First, compute the two sides of the Curl Theorem as directly as possible, and check equality.
     2. Starting our proof requires regions which are both x-simple and y-simple (see M&T p. 283). Split R into two such regions R = R₁ ∪ R₂, joined along a common boundary line.
        Hint: As an inverse for y = x² + 1, use the function b(y) = √(y−1) for y ≥ 1,   b(y) = 0 for y ≤ 1.
     3. Simplify ∬_Ri (^∂Q⁄_∂x − ^∂P⁄_∂y) dy dx for each simple region R₁, R₂. Rather than computing out all the integrals and derivatives, consider the terms ∬_Ri ^∂Q⁄_∂x dx dy and −∬_Ri ^∂P⁄_∂y dy dx separately, and use the one-variable Fundamental Theorem of Calculus.
     4. Rewrite the above terms of the line integrals ∮_ci F • dc_i = ∮_ci P dx + ∮_ci Q dy, where c₁, c₂ are the boundaries of the two regions.
     5. Explain why the sum of the line integrals for the two boundaries is equal to the line integral for the boundary of R. (What happens to the integral over the extra line between the regions?)
  2. Give a proof of the Divergence Theorem by mimicking our proof of the Curl Theorem. (As discussed above, the Curl Theorem implies the Divergence Theorem by simply substituting F^⊥ for F. Nevertheless, prove the second theorem without assuming the first.)
  3. If F is a vector field with curl(F) = 1 for all (x,y), then the Curl Theorem says that the area of the region R is equal to the line integral of F over the boundary curve of R.
     1. Let F = ½(−y, x), and let R be the region given in polar coordinates by r ≤ f(θ), for some function f. Use the Curl Theorem to give a simple formula for the area of R. Obtain the same formula directly using the polar change of variables.
     2. M&T p. 437 #13. Find the area under one arch of the cycloid curve (x,y) = (t−sin(t), 1−cos(t)) by computing the line integral of: F(x,y) = (0, x); or (−y,0); or ½(−y, x). Which vector field gives the simplest computation?
  ⊞ Solutions

  1a. From the picture of F(x,y) = (x+1, xy), we can see that curl(F) > 0 on the whole region. Also, F • c' is positive on the left, bottom, and right boundaries of R, while it is moderately negative on the top boundary (oriented right-to-left); thus the total rotation around the boundary should be positive.

  Computing the left side of the Curl Theorem, with curl(F) = y − 0:

  ∬_R curl(F) dy dx  =  ∫₋₁¹ ∫₀^1+x2 y dy dx  =  ∫₋₁¹ ½(1+x²)² dx  =  ²⁸⁄₁₅ .
  Computing the right side of the Curl Theorem for the four counter-clockwise boundary curves of R:

  ∮ F • dc	=	∫−11 F(t,0) • (t,0)' dt + ∫02 F(1,t) • (1,t)' dt
  		+ ∫1−1 F(t,1+t2) • (t,1+t2)' dt + ∫20 F(−1,t) • (−1,t)' dt
  	=	∫−11 (t+1,0) • (1,0) dt + ∫02 (2,t) • (0,1) dt
  		+ ∫1−1 (t+1,t+t3) • (1,2t) dt + ∫20 (0,−t) • (0,1) dt
  	=	2 + 2 − 62⁄15 + 2  =  28⁄15.

  Notice that we parametrized the left boundary curve as c₄(t) = (−1, t) from the top corner t = 2 to the bottom corner t = 0, giving reversed limits of integration ∫₂⁰. (Similarly with the top curve.)

  1b. Split the region along the y-axis so that each half is doubly simple, with no vertical or horizontal bays or dents:

  R₁ = {(x,y) with 0 ≤ x ≤ 1, 0 ≤ y ≤ 1+x²} = {(x,y) with 0 ≤ y ≤ 2, b(y) ≤ x ≤ 1},

  R₂ = {(x,y) with −1 ≤ x ≤ 0, 0 ≤ y ≤ 1+x²} = {(x,y) with 0 ≤ y ≤ 2, −1 ≤ x ≤ −b(y)},

  where b(y) = √(y−1) for y ≥ 1 and b(y) = 0 for y ≤ 1.

  1c. For the region R₁, and F = (P,Q) = (x+1, xy), the curl integral is:

  ∬R1 curl(F) dy dx	=	∬R1 (∂Q⁄∂x − ∂P⁄∂y) dy dx
  	=	∫ y=0 2 ∫ x=b(y) 1 ∂⁄∂x(xy) dx dy  −  ∫ x=0 1 ∫ y=0 x2+1 ∂⁄∂y(x+1) dy dx
  	=	∫ y=0 2 [xy]x=b(y) x=1 dy  −  ∫ x=0 1 [x+1]y=0 x2+1 dx
  	=	∫ y=0 2 1y − b(y)y dy  −  ∫ x=0 1 (x+1) − (x+1) dx.
  	=	∫ y=0 2 Q(1,y) − Q(b(y),y) dy  −  ∫ x=0 1 P(x,x2+1) − P(x,0) dx.

  We have a similar computation for R₂.

  1d. The line integral over the boundary curve c₁ = (x(t), y(t)) is: ∮ F • dc₁  =  ∮ (P(c₁),0) • dc₁+ ∮ (0,Q(c)) • dc₁
   =  ∫ P(x(t),y(t)) x'(t) dt + ∫ Q(x(t),y(t)) y'(t). For the P-term, we parametrize the boundary of R₁ by four segments consistent with its y-simple description: (x(t),y(t))  =  (t,0), (1,t), (t,t²+1), (0,t), the last two traveled in reverse. For the Q-term, we parametrize the same boundary consistently with the x-simple description: (x(t),y(t))  =  (t,0), (1,t), (t,b(t)), with the last traveled in reverse. Then we may compute:

  ∮ (P(c1),0) • dc1+ ∮ (0,Q(c)) • dc1	=	∫01 P(t,0) (t)' + ∫02 P(1,t) (1)' + ∫10 P(t,t2+1) (t)' dt + ∫10 P(0,t) (0)' dt
  		+ ∫01 Q(t,0) (0)' + ∫02 Q(1,t) (t)' + ∫20 Q(t,b(t)) (t)' dt.

  The vertical and horizontal terms containing (1)' and (0)' all vanish, and the remaining four terms match those at the end of 1(c).
  This proves the Curl Theorem for region R₁, and the proof for R₂ is similar.

  1e. Assume we know the Curl Theorem for the two regions R₁ and R₂. Adding the double integrals on the left side of the Theorem for R₁ and R₂, we clearly get the double integral over R. Adding the line integrals along the two boundary curves, we get the line integral over the boundary of R, plus the line integral along the boundary line separating the subregions, taken twice in opposite directions, which cancel out. The left side equals the right side over the whole region R.

  3a. For F = ½(−y,x), we easily calculate curl F = 1, so the left side of the Curl Theorem gives the area of the region. The right side is the line integral of F along the boundary curve given by (r,θ) = (f(t),t), namely c(t) = (f(t)cos(t), f(t)sin(t)): ∮ F(c) • dc  =  ∫_t=0^2π ½(−f(t)sin(t), f(t)cos(t)) • (f(t)cos(t), f(t)sin(t))' dt  =  ∫_t=0^2π ½ f(t)² dt. This can also be obtained from parametrizing R by the polar coordinate map T(r,θ) = (r cos(θ), r sin(θ)) for (r,θ) in the parameter region defined by 0 ≤ θ ≤ 2π, 0 ≤ r ≤ f(θ); then using the Change of Variables formula.

• ⊞ 4/28: Recitation problems: solids, volume and surface area.
  HW: For each solid below, determine:

  1. Volume using rectangular coordinates (taking an appropriate order of integration)
  2. Volume using a cylindrical (or elliptic cylindrical) parametrization
  3. Surface area using any convenient parametrization.

  The solids are constructed from specified slices at a given position.

  1. The solid built above the a unit circle in the xy-plane from square slices on the line segments defined by x = a, a^2 + y^2 ≤ 1.
     Hint: This solid is an intersection of a vertical circular cylinder and a horizontal parabolic cylinnder: its surface can be constructed out of paper.
  2. The "pillow" solid whose slice at height z is the ellipse (^x⁄_z²−1)² + y² ≤ 1.

• ⊞ Final Review Problems
  1. Consider the region R inside the cone (x−z)² + y² ≤ z², above z = 0, and below the plane z = 2 − ½x.
     1. Describe the horizontal slices of the bottom surface (x−z)² + y² = z², holding z constant. Sketch these slices in 3 dimensions, forming the surface of a tilted cone. Hint: The slices are circles.
     2. The edge curve of R is given by the intersection of the lower surface (x−z)² + y² = z² and the upper surface z = 2 − ½x. Describe the xy-shadow under this curve. Hint: It is an ellipse.
     3. Describe R as a z-simple region above its xy-shadow.
     4. Use the above description of R to set up integrals for the volume and surface area of R.
     5. Parametrize R by tilted cylindrical coordinates. Start by parametrizing the xy-shadow ellipse by translating and squashing polar coordinates; then deduce the (x,y,z) coordinates of the top surface; then multiply by a scale parameter s to get (sx, sy, sz), the slices parallel to the top surface.
        The result was used to make this picture of R:
     6. Use the above cylindrical parametrization to set up new integrals for the volume and surface area of R.
  2. Let f(x,y,z) = (x-1)² + y² + z², the square distance of (x,y,z) from (1,0,0).
     1. From the picture, estimate the critical and constrained critical points of f on R and ∂R.
     2. Find the critical points by solving ∇f(v) = 0 for v ∈ R.
     3. Find the constrained critical points by solving ∇f(v) = λ ∇g(v), for a scalar λ and v ∈ ∂R, where g(x,y,z) = (x−z)² + y² − z² (lower surface contour) or g(x,y,z) = 2 − ½x − z (upper surface countour).
     4. Find the critical points on the edge-curve between the surfaces by parametrizing it as c(t) and solving f(c(t))' = 0.
     5. Determine the max and min points and values of f on R.
  3. For the above f, let F = ∇f.
     1. Sketch this vector field.
     2. Find div F and curl F, and explain why the answers are expected.
     3. Determine the integral of div F over R.
     4. Determine the flux of F through ∂R. Explain why the result is the same as the previous integral.

• ⊞ X/XX: Lect X. Z.Z Chapter name.
  Class notes. See the Weekly HW due X/YY below.
  HW:

  1. Setup
     1. Problem
  ⊞ Solutions

  1a. Answer

• ⊞ HTML Examples
  
  k   c
  ∑ _k=1 ⁿ⁻¹ (n | k)
  

  

• ⊞ **Ch. 6.1**  
  HW: Linear mappings of R and R², matrices, rotations and reflections.

  1. Find the matrix [L] for each of the linear mappings L : R² → R² below. That is, the 2×2 matrix whose columns are the vector matrices [l(i)] = [l(1,0)] and [l(j)] = [l(0,1)].
     1. L(v) = v, the identity mapping which takes each vector to itself.
     2. L = R_θ, rotation by angle θ counterclockwise.
     3. L = R _−θ, rotation by angle θ clockwise.
     4. L = R _−θ ° R_θ, the composite mapping which rotates by θ, then rotates back. (You should multiply the matrices from the previous two problems according to the row • column definition.)   Simplify using a trig identity, and explain why the result makes sense geometrically.
     5. L = R_α ° R_β, the composite of rotating by angle β, then by α.
     6. L = R_α+β. Geometry tells us this is the same mapping as the previous. Compare the resulting matrices to prove the angle sum identities in trigonometry.
  2. A linear mapping L : Rⁿ → R^m, between any dimensions of space, is determined by an m×n matrix [L], with m rows and n columns. We can compute its outputs through the matrix product [L(v)] = [L] • [v].
     1. Write the 1×2 matrix of the linear mapping ℓ(x,y) = 2x + 3y. The columns of this matrix are just the numbers ℓ(i) = ℓ(1,0) and ℓ(j) = ℓ(0,1). Check that [ℓ(v)] = [ℓ] • [v].
     2. What is the general form of a linear mapping L : R → R² ? What is its matrix like?
     3. What is the general form of a linear mapping ℓ : R → R? What is its matrix like?
  3. For each of the following matrices, geometrically describe the corresponding linear mapping.

     a.

     0   1   1   0

     b.

     3   0   0   3

     c.

     1   1   0   1

     Hint: For (c), describe how the mapping distorts a unit square, by considering the consecutive corners L(0,0), L(1,0), L(1,1), L(1,0). It is called a shear mapping.
  ⊞ Solutions
  Since column matrices are hard to display, we denote the column matrix of a vector v = (x,y) by: [v] = [x,y]^T,

  where the transpose operation ^T flips a 1×2 row matrix over to a 2×1 column matrix.

  1. Matrices of the given linear mappings.

  a.

  1   0   0   1

  b.

  cos(θ)   −sin(θ)   sin(θ)   cos(θ)

  c.

  cos(θ)   sin(θ)   −sin(θ)   cos(θ)

  d.

  cos²(θ) + sin²(θ)   0   0   cos²(θ) + sin²(θ)

  Since cos²(θ) + sin²(θ) = 1, this is just the identity matrix from part (a). This makes sense, since one rotation undoes the other, taking each vector back to itself.

  e. Product of matrices:

  cos(α)   −sin(α)   sin(α)   cos(α)

  •

  cos(β)   −sin(β)   sin(β)   cos(β)

  =

  cos(α)cos(β) −sin(α)sin(β)   − cos(α)sin(β) −sin(α)cos(β)    sin(α)cos(β) +cos(α)sin(β)    −sin(α)sin(β) +cos(α)cos(β)

  e.

  cos(α+β)   −sin(α+β)   sin(α+β)   cos(α+β)

  Equating with the entries in (e) gives: cos(α+β) = cos(α)cos(β) − sin(α)sin(β) sin(α+β) = sin(α)cos(β) + cos(α)sin(β). This is the "real reason" for the angle-sum trig identities.

  2a. The matrix of ℓ : R² consists of columns given by the outputs of the function on the standard basis vectors of the input space R², namely ℓ(i) = ℓ(1,0) = 2 and ℓ(j) = ℓ(0,1) = 3, so [ℓ] = [2,3].
  To check this is correct, we compute: [ℓ(v)] = [ℓ] • [v] = [2,3] • [x,y]^T = 2x + 3y. Note that the matrix product (row • column) is the same as the dot product of vectors (2,3) • (x,y).

  2b. A general linear mapping L : R → R² is of the form L(x) = (ax, bx), with each component a linear mapping R → R. Its matrix is the column given by the output of the standard basis vector e of the input space R, which is just the number v = 1; that is, [L] = [L(e)] = [L(1)] = [a,b]^T.

  2c. A general linear mapping R → R is ℓ(x) = ax, with 1×1 matrix [ℓ] = [a].

  3a. Computing [L(x,y)] = [L] • [x,y]^T, we get L(x,y) = (y,x), which is a reflection across the diagonal y = x. (This is the mapping which flips a graph y = f(x) over to the graph of the inverse function y = f⁻¹(x).)

  3b. L(x,y) = (3x, 3y), or L(v) = 3v, stretches each vector by a factor of 3.

  3c. The shear mapping L(x,y) = (x, x+y) slants the unit square into the rhombus (diamond) with consecutive corners (0,0), (1,0), (1,2), (1,1). It does the same slanting to whole grid of R². Although this mapping stretches and squashes angles, it does not distort area since the determinant of its matrix is 1.

• ⊞ HW due 1/15: Thales' Theorem
  Thales' Theorem in geometry states that if you inscribe a triangle in a half-circle, with one side of the triangle equal to the diameter of the circle, then the angle opposite that side is a right angle. Prove this by vector algebra.

  • State the proposition to be proved, making clear the hypothesis (the setup or "if" part), and the conclusion (the payoff or "then" part).
  • Start the proof by translating the geometric terms in the hypothesis into vector language. Taking the center of the circle to be the origin, let one end of the diameter be v (what is the other end?), and let the third vertex of the triangle be u.
  • Write the vector formula which states that u and v lie on the same circle.
  • Find the two vectors defining the sides of the triangle from u.
  • Use the dot product to test these vectors for orthogonality. Carefully expand using the known properties of the dot product, such as commutativity and the distributive law.
  • Using the assumptions in the hypothesis, show that orthogonality does indeed hold, and translate back into geometric language.
  • Here is a model proof for HW 1/11 #2 above.
  • You may turn in hand-written proofs, but a good tool to learn is Latex, which you can download free.
  • Solution

• ⊞ HW due 1/22: Graph landscape
  Construct a function f : R² → R whose graph z = f(x,y) makes an interesting landscape. Some hints:

  • Graph the one-variable bump functions g(r) = ¹⁄_(1+r²) , ¹⁄_(1+|r|) , e^−r2 (Wolfram|Alpha: plot e^(-r^2) for r=-2.5 to 2.5). Turn each of these into a mountain by taking its surface of revolution around the vertical axis, namely the graph of the two-variable function f(x,y) = g(√(x²+y²)) (W|A: plot3d 1/(1+sqrt(x^2+y^2)) for x = -2 to 2 and y = -2 to 2).
  • Experiment with other g(r). How would you get a long ridge with a given cross-section? Ans: f(x,y) = e^{-x^2}. What is going on with: f(x,y) = exp(−(y−sin(x))²)?
  • Experiment with the effect of taking f(x−a, y−b) and f(ax, bx) for some constants a,b. Superimpose several mountains and valleys by adding and subtracting such functions. Try multiplying functions: exp(−x²−y²) * sin(x) scales the waves of f(x,y) = sin(x) by the bump function exp(−x²−y²). Taking the square root of a positive function produces cusps at the zero points: egg-crate function f(x,y) = −√(2−cos(x)−cos(y)). Be artistic.
  • Find the (x,y) window which best shows the interesting features of your function. In addition to the graph, take the contour plot and gradient vector field. It is probably best to draw the gradient vectors by hand onto the contour plot: remember that the closer the contours, the longer the gradient (since its length is the uphill slope).
  • Once you have your function, locate its critical points, where ∇f(x,y) = (0,0). (W|A will solve the equations for you most of the time.) Classify each as a max (hill like z = x²+y²), min (valley like −x²−y²) or saddle (like x²−y²), or possibly a ridge. Note how each of these looks on the countour plot and gradient field.
  • You might want to pay $6 for a month of Wolfram|Alpha Pro, which makes W|A work a good deal better (for example, it accepts long inputs).

  Turn in:

  1. Printout of your graph, countour plot and vector field (copy and paste the W|A images).
  2. Clear description of how you built up the formula for your function from its basic elements.
  3. Classification of the critical points.

• ⊞ HW due 1/29: Curl = rate of rotation
  Prove that, as claimed in class, curl F measures the rate of rotation of F around a point, per area enclosed. That is, for a vector field F(x,y) = (p(x,y), q(x,y)), the limit of the line integral around a small rectangle near (x,y), divided by the rectangle's area, approaches curl F(x,y):

  lim_{Δx,Δy → 0}   ¹⁄_ΔxΔy   ∮ F(c_ΔxΔy) • dc_ΔxΔy   =   ^∂q⁄_∂x(x,y) − ^∂p⁄_∂y(x,y) ,

  where c_ΔxΔy(t) is the curve which traces around a rectangle from (x,y) to (x+Δx, y) to (x+Δx, y+Δx) to (x, y+Δy) and back to (x,y).

  • To evaluate the left side, use the computational definition of line integral: ∮ F(c) dc = ∫^s_r F(c(t)) • c'(t) dt, where the curve's parameter goes through the interval s ≤ t ≤ r.
  • Get your preliminary answer in terms of certain antiderivative functions: P(x,y) with ^∂P⁄_∂x = p(x,y), and Q(x,y) with ^∂Q⁄_∂y = q(x,y). What does the First Fundamental Theorem of Calculus say about these?
  • After you evaluate the line integral, take the limit as Δx → 0, then Δy → 0, or perhaps in the other order.
  • You might need the fact that partial derivatives commute: ^∂⁄_∂x ^∂⁄_∂y f(x,y)  =  ^∂⁄_∂y ^∂⁄_∂x f(x,y), so it does not matter which derivative you take first.

• ⊞ HW due 2/5: Laws of vector algebra
  In abstract algebra, we consider not only the familiar arithmetic operations, but more general operations on more general types of "numbers", such as our operations on vectors. Let A be some set of objects which can be combined by an operation ∗, so that for any elements a,b, we get a new element c = a ∗ b. We list several familiar properties which may or may not hold for our operation:

  1. Associative:   (a ∗ b) ∗ c  =  a ∗ (b ∗ c)
  2. Identity Element: There is an element e which has no effect on any a: e ∗ a  =  a ∗ e  =  a.
  3. Inverses: For any a, there is some b which cancels it: a ∗ b  =  b ∗ a  =  e.
  4. Commutative:    a ∗ b  =  b ∗ a.
  5. Distributive: We can define an extra operation ⊕ with: a ∗ (b ⊕ b')  =  a∗b  ⊕  a∗b' ,
     (a ⊕ a') ∗ b  =  a∗b  ⊕  a'∗b .

  Generalizing even more, the ∗ operation may combine two different kinds of objects (such as a scalar times a vector), and may produce yet another kind of object (such as the dot product of vectors producing a scalar). Thus, we might have three sets A, B, C with a ∗ b  =  c for a ∈ A, b ∈ B, c ∈ C.

  Problem: For each of the following operations, state whether it obeys each property (i)−(v), and prove your answer.

  1. Vector addition:  A = B = C = R³,   a ∗ b  =  a + b.
  2. Scalar multiplication:  A = R , B = C = R³,   a ∗ b  =  ab.
  3. Dot product:  A = B = R³, C = R,  a ∗ b  =  a • b.
  4. Cross product:  A = B = C = R³,  a ∗ b  =  a × b det(u⁽¹⁾, v⁽¹⁾) i  −  det(u⁽²⁾, v⁽²⁾) j  +  det(u⁽³⁾, v⁽³⁾)) k.
     For cross product only, also check these weird variations, known as Lie algebra properties:
     • iv'. Anti-commutative:  a × b  =  − b × a
     • v'. Jacobi identity:  a × (b × c)  =  (a × b) × c   +   b × (a × c).
  5. Extra Credit: Min-plus algebra:  A = B = C = R ∪ {∞},  a ∗ b  =  a + b, and a ∗ ∞ = ∞ ∗ a = ∞.
     
     • Here ∞ is a symbol which is formally larger than any real number.
     • For the Distributive property, we define the extra operation a ⊕ b = min(a,b), the smaller of the two numbers.
     • Thus, + takes the usual role of multiplication, and min takes the usual role of addition. This weird structure is also called the tropical algebra; it is very useful in computer science and algebraic geometry.

  Hints:

  • If a property does not hold, you can usually prove it with a counterexample. For example, to prove the Commutative property fails, it is enough to compute a ∗ b ≠ b ∗ a for some particular a,b.
  • However, to prove the Identity Element property fails, you must show that no possible element e satisfies the equation a ∗ e = e ∗ a = a. (This makes no sense for dot product, but a partial version of Identity Element does hold.)
  • To prove a property holds, you can usually use the corresponding property of ordinary arithmetic, which we take for granted. For example, to show that vector addition is Commutative, we compute for any a, b: a + b = (a₁ + b₁, a₂ + b₂, a₃ + b₃)
    = (b₁ + a₁, b₂ + a₂, b₃ + a₃) = b + a, where the first and last equalities are by definition, and the middle equality holds because in each component we know that a + b = b + a for real numbers a,b.
  • To consider the Distributive property, you must define an appropriate ⊕ operation to add two elements in A, in B, or in C. If there is no obvious ⊕ operation, say so.
  • To prove properties of cross-product, you may assume the usual properties of 2-dimensional det used to define it.
  • The Jacobi identity (i.e. Jacobi formula), a weird mashup of Associative and Distributive properties, is nasty to check directly. Show that if it holds for the triple a', b, c and the triple a", b, c, then it holds for a, b, c where a = s' a' + s" a"; and similarly if we split up vectors b and c. (We say that the formula is linear in each variable.) Now it is enough to check the formula for a, b, c each chosen from the standard basis vectors i, j, k.
  • It is good style to prove formulas via a single chain of equalities, as above. However, to build this chain in your rough draft, you might want to work forwards from the left side, backwards from the right side, and try to meet somewhere in between. Don't tell the story of your discovery process in the final proof, just give the straight chain of equalities or logical deductions.
  • Consider your audience to be one of your classmates who have not done this assignment. Explain just enough for them to understand the reasoning, and skip steps they would consider obvious. The first three operations are straightforward, and should take a half page each.

• ⊞ HW due 3/3: Optimizing a Sawmill

• HW due 3/25: Models of Solids

• ⊞ HW due Wed 4/27: Divergence Theorem
  • State the Divergence Theorem in Two Dimensions (Green-Gauss Theorem) for a vector field F over a plane region R: in words, in a compact integral formula, and in coordinates with F(x,y) = (P(x,y), Q(x,y)).
  • Prove the special case when F = (0, Q) and the region R is y-simple.
  • Prove the special case when F = (P, 0) and R is x-simple.
  • Prove the case when F is arbitrary, and R is both x- and y-simple.
  • Prove the case when F is arbitrary, and R is divided into two simple regions R₁ and R₂ along a common boundary curve c.
  • Prove the case when R is built up of many simple regions, using induction to add one region at a time along a common boundary.

• Review notes on Calculus I and Calculus II.

• Notes 1/11: Plane Vectors

• Surface plotter

• ⊞ Notes 1/15: Gradient Theorem
  Handwritten notes. Wikipedia on line integrals, Gradient Theorem.

  • Parametrized curve: c(t) = (x(t), y(t)) gives the (x,y)-coordinates of a moving point over time, starting at c(0) and usually ending at c(1). Formally, a function c : [0,1] → R², where [0,1] is the interval with 0 ≤ t ≤ 1.
  • Tangent vector: velocity c'(t) = (x'(t), y'(t)) = lim_{s → t} (c(s) − c(t)) / (s − t). For s near a fixed t, we have the linear approximation:
    c(s)   ≈   c(t) + (s−t) c'(t).

  • Line integral of a vector field F(x,y) along a curve c is defined as:
    ∮ F(c) • dc   =   lim_n→∞ ∑ⁿ_i=1 F(c_i) • Δc_i ,

    where we split the curve by sample points c_i = c(ⁱ⁄_n) going from the start point c₀ = c(0) to the endpoint c_n = c(1), and Δc_i = c_i − c_i−1 .

  • To compute a line integral, we use the approximation:
    Δc_i   ≈   c' (ⁱ⁻¹⁄_n) Δt,

    where Δt = ¹⁄_n. Taking the limit as n → ∞ gives:

    ∮ F(c) • dc   =   ∫₀¹ F(c(t)) • c'(t) dt,

    which is the ordinary integral of the scalar function F(c(t)) • c'(t) over the interval t = 0 to t = 1.

  • The motivation for the line integral is to reconstruct a scalar function from its gradient vector field.

    Gradient Theorem: Suppose F = ∇f is the gradient vector field of a scalar function f(x,y), and c(t) is a parametrized curve between points c(0) and c(1). Then the line integral of the gradient field is the total change of f from the start to the end point of the curve:

    ∮ ∇f(c) • dc   =   f(c(1)) − f(c(0)).

    Thus, if we are given the initial value f(0,0), we take the line integral over a curve from c(0) = (0,0) to c(1) = (a,b) to find the potential function:

    f(a,b)   =   f(0,0) + ∮ ∇f(c) • dc.   =   f(0,0) + ∫₀¹ ∇f(c(t)) • c'(t) dt.

    Note that we may use any curve c(t) from (0,0) to (a,b).

  • Example: For the vector field F(x,y) = (y,x) along the straight-line path c(t) = (2t, 3t) from (0,0) to (2,3), we have c'(t) = ^d⁄_dt(2t, 3t) = (2,3), and we compute:
    ∮ F(c) • dc   =   ∫₀¹ F(c(t)) • c'(t) dt   =   ∫₀¹ F(2t, 3t) • (2,3) dt

      =   ∫₀¹ (3t, 2t) • (2,3) dt   =   ∫₀¹ 12t dt,   =   6t² |¹_t=0   =   6.

    Thus, if F = ∇f is the gradient field of some function f(x,y) with f(0,0) = 0, we must have f(2,3) = f(0,0) + ∮ F(c) • dc = 6.

    Doing the same computation over a line c(t) = (at, bt) from (0,0) to (a,b), we end up with: f(a,b) = ab, so that f(x,y) = xy. Indeed, we check: ∇f(x,y) = (^∂⁄_∂x(xy), ^∂⁄_∂y(xy)) = (y,x).

• ⊞ Notes 1/20−22: Potential, curl, double integral, Green-Stokes Theorem
  Handwritten notes.

  • Potential: If a vector field F is a gradient, F = ∇f, we say that f is a potential function for F. Not every vector field can have a potential function, as we have seen in exercises. In fact, we have the following equivalence of statements:
    • F has a potential function f.
    • F is irrotational: the line integral ∮ F(c) dc = 0 around any closed curve c(t), a loop with c(0) = c(1).
    • F is path independent: the line integral of F between any two points d and e does not depend on the path chosen; that is, ∮ F(c₁) dc₁  =  ∮ F(c₂) dc₂ for any two curves c₁, c₂ from d to e.

    It is easy to see that a potential function F = ∇f implies that F is irrotational, since the Gradient Theorem says that ∮ F(c) dc is the total change in the height of f from the beginning to the end of c, which is zero if c is a loop. Further, irrotational is equivalent to path independent, since a pair of paths from d to e is equivalent to the loop c formed by going from d to e along c₁, then back along c₂, and ∮ F(c) dc  =  ∮ F(c₁) dc₁ − ∮ F(c₂) dc₂ . The only unclear question is why a path-independent line integral always gives a valid potential function.

  • Curl: For a vector field F(x,y) = (p(x,y), q(x,y)), we define its curl as a scalar function (curl F) : R² → R in terms of the partial derivatives of its components:
    curl F(x,y)   =   ^∂q⁄_∂x − ^∂p⁄_∂y

    Geometrically, curl F measures the rate of rotation of F around a point (x,y) = (a,b), relative to the area enclosed in a small region around (a,b):

    curl F(a,b)   =   lim_{R → (a,b)} ( ∮ F(c) • dc ) / area(R) ,

    where the limit is over smaller and smaller regions R containing (a,b), and c is the counterclockwise boundary curve of R.

  • In fact, a vector field F is irrotational (and has a potential function f) if and only if curl F = 0 everywhere. This is intuitive: a field has zero line integral around any closed curve whenever it has zero rate of rotation around any point. The Green-Stokes Theorem below formalizes this argument.

  • Example: The field F(x,y) = (0, ¹⁄_(1+x²)) could represent the velocity of a river flowing strongest along the middle (the y-axis):
    

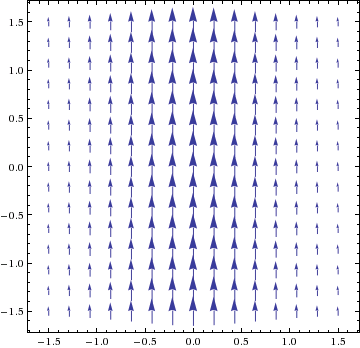
    A small paddlewheel placed at (x,y) = (1, 0) would feel a stronger upward push on its left side than on its right, and would turn clockwise, so the field has negative curl at this point. At (x,y) = (−1, 0), it would turn counterclockwise, which means positive curl.
    We compute: curl F(x,y) = ^∂⁄_∂x(¹⁄_(1+x²)) − ^∂⁄_∂x(0)  =  ^−2x⁄_(1+x²)²) , and we verify that curl F(1, 0) = −½, and F(−1, 0) = ½.

  • Double integral: For a function f(x,y), we define ∬_R f(x,y) dA to be the volume under the graph z = f(x,y) and above the plane region R. Here dA = dx dy represents an increment of area in R, and volume under the xy-plane, where f(x,y) < 0, counts as negative.
    To compute this, write R as the region between two graphs y = g(x) and y = h(x), and two vertical lines x = a and x = b, namely: R = { (x,y) with a ≤ x ≤ b and g(x) ≤ y ≤ h(x) }. Then the double integral is an iterated integral, in which we first integrate with respect to the y variable, considering x as a constant, then integrate the resulting function with respect to x.
    ∬_R f(x,y) dA  =  ∫^b _a ( ∫^h(x) _g(x) f(x,y) dy ) dx

    Of course, we can also switch the roles of x and y.

  • Example: Let R be the triangle in the first quandrant bounded by the line x + y = 1, and take f(x,y) = 1−x²−y², whose graph is an inverted paraboloid above the triangle. The region can be written: R = { (x,y) with 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1−x }. The volume under the graph is:
    ∬_R f(x,y) dA  =  ∫¹ _x=0 ( ∫^1−x _y=0 1−x²−y² dy ) dx

    = ∫¹_x=0 ( y − x²y − ¹⁄₃ y³ |^1−x _y=0 ) dx

    =   ∫¹_x=0 (1−x) − x²(1−x) − ¹⁄₃(1−x)³ dx  =  ¹⁄₆ .

  • Green-Stokes Theorem (Curl Theorem): For a vector field F, the double integral of the rate of rotation of F over a region R is equal to the total rotation of F around the boundary of R:
    ∬_R curl F dA   =   ∮ F(c) • dc .

    Here the closed curve c must not cross itself, and it must go counterclockwise enclosing R, a region with no holes or points where curl F is undefined.

    The intuitive explanation is that the rotation line integral on the right side can be split over a grid of subregions whose rotations cancel each other along their common boundaries, except along the outside boundary of R. As the grid gets finer and finer, each small line integral near (x,y) is approximated by curl F(x,y) dA, and their sum approaches the double integral on the left side.

  • Example: Consider the previous F(x,y) = (0, ¹⁄_(1+x²)) over the square region R = {(x,y) with 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1}. The double integral of the rate of rotation (the curl of F) over the region is:
    ∬_R curl F dA   =   ∬_R ^−2x⁄_(1+x²)² dA   =   ∫¹₀ ∫¹₀ ^−2x⁄_(1+x²)² dy dx

      =   ∫¹₀ ( ^−2xy⁄_(1+x²)² |¹ _y=0 ) dx   =   ∫¹₀ ^−2x⁄_(1+x²)² dx   =   ⁻¹⁄₂ .

    The boundary of R consists of the line segments c₁(t) = (t,0), c₂(t) = (1,t), c₃(t) = (1−t,1), c₄(t) = (0,1−t) for 0 ≤ t ≤ 1; and the total rotation is the line integral:

    ∮ F(c) • dc   =   ∮ F(c₁) • dc₁ + ∮ F(c₂) • dc₂ + ∮ F(c₃) • dc₃ + ∮ F(c₄) • dc₄
      =   0 + ¹⁄₂ + 0 − 1   =   ⁻¹⁄₂ .

    In detail, one of these is:

    ∮ F(c₄) • dc₄   =   ∫¹₀ F(0,1−t) • (0,1−t)' dt   =   ∫¹₀ (0, ¹⁄_(1+0²)) • (0,−1) dt   =   −1.

• ⊞ Notes 1/25: Flux, divergence, Green-Gauss Theorem
  • Flux integral. The flux of a vector field F across a curve c is the net flow of F from the left to the right side of c. By this we mean that c(t) = (x(t), y(t)) has velocity vector c'(t) = (x'(t), y'(t)), whose counterclockwise orthogonal c'(t)^⊥ = (−y'(t), x'(t)) points to the left side of c; and the opposite n(t) = −c'(t)^⊥ = (y'(t), −x'(t)) is called the normal vector, and points to the right side of c.

    To see how strongly the field F is flowing across the curve c at a given point, we take the the dot product of F(c(t)) • n(t). The flux is the line integral of this quantity:

    flux  =  ∮ F(c) • dn  =  ∮ F(c) • (−dc^⊥)  =  ∫¹₀ F(c(t)) • (−c'(t)^⊥) dt

    We can also define it (and compute it numerically) as a Rienmann sum:

    ∮ F(c) • dn  =  lim_n→∞ ∑ⁿ_i=1 F(c_i) • (−Δc_i^⊥),

    where we take sample points c₁,...,c_n on the curve c, and Δc_i = c_i−c_i−1 .

  • Divergence: For a vector field F(x,y) = (p(x,y), q(x,y)), we define its divergence as a scalar function (div F) : R² → R in terms of the partial derivatives of its components:
    div F(x,y)   =   ^∂p⁄_∂x + ^∂q⁄_∂y .

    Geometrically, div F(a,b) measures the rate of outflow of F from a small region near (x,y) = (a,b), relative to the area of the region:

    div F(a,b)   =   lim_{R → (a,b)} ( ∮ F(c) • dn ) / area(R) ,

    where the limit is over smaller and smaller regions R containing (a,b), and dn(t) = −dc(t)^⊥ is the outward normal of the counterclockwise boundary curve c(t) of R.

  • Example: The field F(x,y) = (¹⁄_(1+x²), 0) could represent the velocity of the Red Cedar River flowing over the dam next to Wells Hall (the y-axis):
    

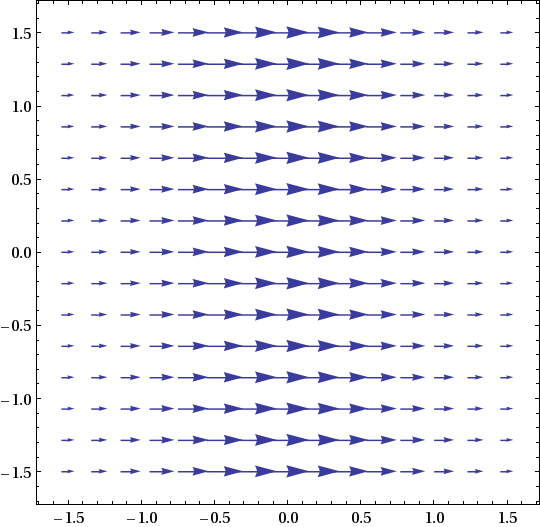
    A small box placed at (x,y) = (−1, 0) would have a weaker inflow across its left boundary and a stronger outflow across its right boundary: this means positive net outflow, positive divergence. (This is compatible with the incompressibility of water because the river gets shallower where it flows faster.)
    We compute: div F(x,y) = ^∂⁄_∂x(¹⁄_(1+x2)) − ^∂⁄_∂x(0)  =  ^−2x⁄_(1+x²)² , and we verify that div F(−1, 0) = ½, and also F(1, 0) = −½.

  • Divergence Theorem (Green-Gauss Theorem): For a vector field F, the double integral of the rate of outflow of F over a region R is equal to the total outflow of F across the boundary of R:
    ∬_R div F dA   =   ∮ F(c) • dn .

    Here the closed curve c must not cross itself, and it must go counterclockwise enclosing R, a region with no holes or points where div F is undefined.

    The intuitive explanation is that the flux line integral on the right side can be split over a grid of subregions whose flux integrals cancel each other along their common boundaries, except along the outside boundary of R. As the grid gets finer and finer, each small line integral near (x,y) is approximated by div F(x,y) dA, and their sum approaches the double integral on the left side.

  • Example: Consider the previous F(x,y) = (¹⁄_(1+x²), 0) over the square region R = {(x,y) with 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1}. The double integral of the rate of outflow (the divergence of F) over the region is:
    ∬_R div F dA   =   ∬_R ^−2x⁄_(1+x²)² dA   =   ∫¹₀ ∫¹₀ ^−2x⁄_(1+x²)² dy dx

      =   ∫¹₀ ( ^−2xy⁄_(1+x²)² |¹ _y=0 ) dx   =   ∫¹₀ ^−2x⁄_(1+x²)² dx   =   ⁻¹⁄₂ .

    The boundary of R consists of the line segments c₁(t) = (t,0), c₂(t) = (1,t), c₃(t) = (1−t,1), c₄(t) = (0,1−t) for 0 ≤ t ≤ 1; and the total flux is the line integral:

    ∮ F(c) • dn   =   ∮ F(c₁) • dn₁ + ∮ F(c₂) • dn₂ + ∮ F(c₃) • dn₃ + ∮ F(c₄) • dn₄
      =   0 + ¹⁄₂ + 0 − 1   =   ⁻¹⁄₂ .

    In detail, one of these is:

    ∮ F(c₄) • dn₄   =   ∫¹₀ F(0,1−t) • (−(0,1−t)')^⊥ dt
      =   ∫¹₀ (¹⁄_(1+0²), 0) • (−(0,−1)^⊥) dt   =   ∫¹₀ (¹⁄_(1+0²), 0) • (−1,0) dt   =   −1.

• ⊞ Notes 2/1: Determinant and cross product for R³
  • det(u, v, w) is a function of three vectors u = (u₁, u₂, u₃), v = (v₁, v₂, v₃), w = (w₁, w₂, w₃), defined recursively in terms of the 2-dimensional determinant: det(p₁, p₂; q₁, q₂) = p₁q₂ − p₂q₁ . Letting v⁽¹⁾ = (v₂, v₃) be the vector v with its first coordinate omitted, and similarly for v⁽²⁾ and v⁽³⁾, we define:
    
    det(u, v, w)   =   u₁ det(v⁽¹⁾, w⁽¹⁾) − u₂ det(v⁽²⁾, w⁽²⁾) − u₃ det(v⁽³⁾, w⁽³⁾).
    Geometrically, this is the volume of the parallelopiped spanned by u, v, w: whose corner at the origin has edges along u, v, w. More precisely, it is the signed volume, meaning it is positive if the vectors make a right-handed triple, negative if left-handed.
  • The determinant has several essential properties which are easy to prove algebraically, and are also clear from its definition as signed volume:
    
    det(u, u, w)  =  0

    det(v, u, w)  =  −det(u, v, w)  =  det(u, w, v)

    det(su + s'u', v, w)  =  s det(u, v, w) + s' det(u', v, w).

  • Cross product: vector × vector = vector. Its essential property is:
    
    det(u, v, w)  =  (u × v) • w.
    That is, u × v is the vector whose dot product with any w is the volume of the parellelopiped spanned by u, v, w. Since we know that:
    
    det(u, v, w)  =  det(w, u, v)  =  det(u⁽¹⁾, v⁽¹⁾) w₁ − det(u⁽²⁾, v⁽²⁾) w₂ + det(u⁽³⁾, v⁽³⁾) w₃,
    the factors in front of w₁, w₂, w₃ must be the coordinates of the cross product:
    
    u × v  =  det(u⁽¹⁾, v⁽¹⁾) i  −  det(u⁽²⁾, v⁽²⁾) j  +  det(u⁽³⁾, v⁽³⁾) k.
    
  • The essential properties of cross product come from those of the determinant: distributivity over vector addition, as well as:
    
    u × u  =  0     and     v × u  =  −u × v,

    u × v is orthogonal to u, v

    u, v, (u × v)  form a right-handed frame.

  • We can write the volume of the (u, v, w)-parallelopiped another way, as the area A of its (u, v) base times the height h of w projected in the direction orthogonal to u, v. The base is the (u, v)-parallelogram, A = area(u, v) = |u| |v| sin(θ_uv) by elementary trigonometry. The height is given by dotting w with the unit orthogonal vector ^{(u × v)}⁄_{|u × v|}, so that h  =  ¹⁄_{|u × v|} (u × v) • w. Thus the volume is:
    
    V  =  (u × v) • w  =  A h  =  ^A⁄_{|u × v|} (u × v) • w.
    We conclude ^A⁄_{|u × v|}  =  1, and:
    
    |u × v|  =  area(u, v)  =  |u| |v| sin(θ_uv) .
    Therefore, u × v is the right-handed orthogonal vector to u and v with length |u| |v| sin(θ_uv).

• Notes 2/5: Limit and derivative theorems

• ⊞ Notes 2/12: Linear mappings, matrix notation, Jacobian matrix
  • The matrix notation for a vector v = (x₁,..., x_n) is [v], a column with row entries x₁,...,x_n:
    [v]   =  

    x1

    ⋮

    xn

    .
    For typographical convenience, we will somtimes write this column vector as [v] = [x₁,...,x_m]^T. (Here T stands for "transpose", meaning we flip a horizontal row vector to a vertical column vector.)
  • A general matrix of dimensions m×n is a table with m rows and n columns, which we may consider as a list of column vectors ℓ₁,...,ℓ_n ∈ R^m:

    L   =   [ ℓ1 | . . . | ℓn ]   =

    |  ℓ1  |   . . .   |  ℓn  |

    .

    
    We can consider a column vector [v] as an m×1 matrix. To specify a matrix L with entry L_ij in row i, column j, we write: L = [L_ij].
  • We define the matrix product of the m×n matrix L with an m×1 column vector [v] as the m×1 column vector of the linear combination x₁ℓ₁ + ... + x_nℓ_n ∈ R^m:
    L • [v]  =  [ ℓ₁ | ... | ℓ_n ] •

    x1

    ⋮

    xn

      =   [x₁ℓ₁ + ... + x_nℓ_n] .
    Another way to think of this is to consider L as a column of row vectors r₁,...,r_m ∈ Rⁿ; then the matrix product is the column vector of dot products r_i • v:

    L • [v]   =

    −   r1   −   ⋮   −   rm   −

    •

    |  v  |

    =

    r1 • v  ⋮  rm • v

    .

    
    (See M&T p. 63.)
  • A linear mapping ℓ : Rⁿ → R^m, between spaces of any dimensions, is a function which respects vector addition and scalar multiplication:
    ℓ(su + tv)   =   s ℓ(u)  +  t ℓ(v) .

    It is determined by the m×n matrix of its outputs on the standard basis vectors of Rⁿ:

    [ ℓ ]  =  [ ℓ(e₁) | ... | ℓ(e_n) ].
    In fact, we can compute the outputs of ℓ through the matrix product:
    [ℓ(v)] = [ ℓ ] • [v] = [x₁ℓ(e₁) + ... + x_nℓ(e_n)] .
    
  • For a function f : Rⁿ → R^m, with f(v) = (f₁(v),..., f_m(v)), its derivative at a point v = c is linear mapping Df : Rⁿ → R^m given by the the Jacobian matrix, the m×n matrix of partial derivatives with row i, column j entry equal to  ^∂f_i(c)⁄_∂xj :

    [Dfc]   =   [ ∂fi(c)⁄∂xj ]   =   [ ∂f⁄∂x1 | . . . | ∂f⁄∂xn ]   =

    ∇f1(c)  ⋮  ∇fm(c)

    .

    
    
  • To get the affine linear approximation of f(v) = f(x₁,...,x_n) near c = (c₁,...,c_n), we write:
    f(v)  ≈  f(c) + Df_c(v−c)   =   f(c) + (x₁−c₁) ^∂f⁄_∂x1(c) + ... + (x_n−c_n) ^∂f⁄_∂xn(c) .
    

• ⊞ Notes 2/15: Matrix multiplication, Chain Rule for general functions
  • Given two linear functions ℓ : Rⁿ → R^m and k : R^m → R^p, we can form their composition or chain, the function k ∘ ℓ : Rⁿ → R^p given by (k ∘ ℓ)(v) = k(ℓ(v)); that is, the output of ℓ becomes the input of k.
  • According to our general rule for linear mappings, the p×n matrix of the composition is:
    [ k ∘ ℓ ]  =  [ k(ℓ(e₁)) | . . . | k(ℓ(e_n)) ]
    
     =  [ [k]•[ℓ(e₁)]  | . . . |  [k]•[ℓ(e_n)] ] .

    That is, we multiply matrix [ k ] by each of the column-vectors of [ ℓ ].

  • To express the composition of linear functions, we generalize the definition of matrix multiplication: p×m matrix K times m×n matrix L is p×n matrix K • L:
    K • L   =   K • [ ℓ₁ | . . . | ℓ_n ]   =   [ K• ℓ₁ | . . . | K• ℓ_n ] .

    That is, we multiply K by each column vector of L. To compute this most conveniently, we take all dot products between the rows of K and the columns of L:

    K • L   =

    −   r1   −   ⋮   −   rp   −

    •

    |  ℓ1  |   . . .   |  ℓn  |

    =

    r1• ℓ1   . . .   r1• ℓn       ⋮ ⋮       rp• ℓ1   . . .   rp• ℓn

    .

    
    With this definition, we evidently have:
    [ k ∘ ℓ ]   =   [ k ] • [ ℓ ] .
    
  • Given two arbitrary functions g : Rⁿ → R^m and f : R^m → R^p, we can again form their composition, the function f ∘ g : Rⁿ → R^p given by (f ∘ g)(v) = f(g(v)). The most general form of the Chain Rule states that the derivative function of the composition is the composition of derivative functions:
    D(f∘g)_c   =   Df_g(c) ∘ Dg_c .

    In terms of Jacobian matrices, this means:

    [ D(f∘g)_c ]   =   [ Df_g(c) ] • [ Dg_c ] .
    The Chain Rule for single-variable functions is just the case where n = m = p = 1, namely: (f∘g)'(c) = f '(g(c)) g'(c); and all other forms of the Chain Rule are also special cases.

• ⊞ Final Review Syllabus
  1. Geometric objects
     • Vector space Rⁿ, vectors v = (x₁,..., x_n) ∈ Rⁿ, with addition, scalar multiplication, dot product. Space R³ also has cross product.
     • Curve C ⊂ Rⁿ defined by:
       • Parameter function c : R → Rⁿ, c(t) over t ∈ [a,b]
       • n−1 contour equations f(v) = c
     • Region R ⊂ Rⁿ (plane or solid) with boundary ∂R, defined by:
       • Simple inequalities: a₁ ≤ x₁ ≤ b₁ , a₂(x₁) ≤ x₂ ≤ b₂(x₁),...
       • Coordinate parameter function T : Rⁿ → Rⁿ, T(u) over u ∈ R* simple parameter region
       • Inequality f(v) ≤ c, with boundary contour f(v) = c
     • Surface S ⊂ R³ with boundary curve ∂S, defined by:
       • Graph z = f(x,y) over (x,y) ∈ S* simple parameter region
       • Parameter function T : R² → R³, T(u) over u ∈ S*
       • Contour equation f(v) = c, cut off by inequalities g(v) ≤ a.
  2. Functions
     • Scalar function f : Rⁿ → R
     • Vector field F : Rⁿ → Rⁿ
     • Parameter/coordinate function T : R^m → Rⁿ
  3. Derivative operations
     • partial derivative ^∂f⁄_∂xi , grad f = ∇f
     • div F = ∇ • F
     • Planar curl (F)  =  curl(P,Q)  =  ^∂Q⁄_∂x − ^∂P⁄_∂y, spatial curl F  =  ∇ × F
     • Tangent vectors from parameter functions: c'(t) or ^∂T⁄_∂x1 , ... , ^∂T⁄_∂xm, each a vector in Rⁿ
     • Jacobian matrix [DT_a]  =  [^∂T⁄_∂x1 | ... | ^∂T⁄_∂xm ],  (n rows) × (m columns)
     • Total derivative linear function DT_a : R^m → Rⁿ with  T(a+v)  ≈  T(a) + DT_a(v)
     • Quadratic Taylor series approximation of f:
       • Hessian matrix H = [ ^∂2f⁄_∂xi∂xj(v) ], n×n
       • column vector [v], (n rows)×(1 column); row vector [v]^tr, (1 row)×(n columns)
       • f(a+v)  ≈  f(a) + [∇f(a)]•[v] + ¹⁄₂ [v]^tr•[H]•[v]
  4. Integral operations
     • Path integral  ∫_C f  |dc| = ∫_a^b f(c(t)) |c'(t)| dt, mass for density f, arclength for f = 1
     • Line integral  ∮_C F • dc  =  ∫ F(c(t)) • c'(t) dt, work done by F pulling along c;
       the rotation of F around a closed curve c.
     • Region integral: mass for density f, surface area or volume for f = 1
       • planar  ∫∫_R f dA  =  ∫∫_R* f(T(u,v)) |det[DT]| du dv
       • spatial  ∫∫∫_R f dV  =  ∫∫∫_R* f(T(u,v,w)) |det[DT]| du dv dw.
     • Surface integral  ∫∫_S f  dA  =  ∫∫_S* f(T) |dn|  =  ∫∫_S* f(T(u,v)) |^∂T⁄_∂u×^∂T⁄_∂v| du dv, mass for density f, surface area for f = 1
     • Flux integral: net flow of F across boundary
       • planar  ∮_C F • dn  =  ∫_a^b F(c(t)) • (−c'(t)^⊥) dt
       • spatial  ∫∫_S F • dn  =  ∫∫_S* F(T(u,v)) • (^∂T⁄_∂u×^∂T⁄_∂v) du dv
  5. Fundamental Theorems of Calculus
     • Gradient Theorem: the integral of the rate of change of f along C is equal to the total change of f.
       ∮_C ∇f • dc  =  f(b) − f(a), where C goes from a to b.
     • Potential Theorem: F has a potential function f with ∇f = F exactly when F is conservative. In this case, f(v) = ∮_C F • dc for any curve C from a fixed a to v.
       F is conservative when any of these equivalent conditions apply:
       • F is path-independent
       • F is irrotational around any closed curve
       • curl F(v) = 0 at all v
     • Divergence Theorem (Gauss): the integral of the rate of outflow of F over a region is equal to the total net outflow of F across the boundary.
       • planar  ∫∫_R div F dA  =  ∮_∂R F • dn
       • spatial  ∫∫∫_S div F dV  =  ∫∫_∂S F • dn
     • Curl Theorem (Stokes): The integral of the rate of rotation of F over a plane region or a surface is equal to the total rotation of F around the boundary.
       • planar  ∫∫_R curl F dA  =  ∮_∂R F • dc
       • spatial  ∫∫_S curl F • dn  =  ∫_∂S F • dc
  6. Max/min of f : Rⁿ → R over region R
     • Critical point inside R: solve ∇f(v) = 0, for v ∈ R
     • Constrained critical point on boundary ∂R: solve ∇f(v) = λ ∇g(v) for λ ∈ R and v ∈ ∂R, where ∂R is defined by contour g(v) = c; or, if ∂R is parametrized by T(u), solve ∇f(T(u)) = 0.
     • Miscellaneous points where ∇f or ∇g is undefined
     • Choose largest and smallest f(v) for v from previous parts: the absolute maximum and minimum points are among these
     • Second-derivative test (optional) for critical point ∇f(v) = 0, using Hessian H
       • if H is positive-definite (all upper-left det > 0), then v is a local minimum
       • if H is negative-definite (−H is positive-definite), then v is a local maximum
       • if H is not pos/neg definite, then v is a saddle or stationary point