7.  Eigenvalues and Determinants

Eigenvalues anddeterminants reveal quite a bit of information about a matrix.  In thislab we will learn how to use MATLAB to compute the eigenvalues,eigenvectors, and the determinant of a matrix. The emphasis will be on eigenvalues rather than determinant, as the former conceptis more useful than the latter - this should become clear through theexercises.

§7.1Determinants

    As you should be aware by now, there is a nice formulafor calculating the determinant of a 2x2 matrix.  Even the 3x3 case is notthat difficult.  But as matrix size increases so does the complexity ofcalculating determinants.  This is where MATLAB, or any other computeralgebra program, comes in.

Example 7.1

Lets start by entering the followingmatrices into MATLAB:

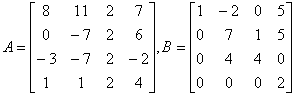
    To compute the determinants of these matrices we aregoing to use the command det().  That is, to computethe determinant of A we type the following

>> det(A)

MATLAB gives us -472 as the answer.  Similarly we get

>> det(B)

ans =

        48

Exercise 7.1
	(a)  Compute the determinant of B by hand. Make sure you leave enough space in your write-up for the calculations. Show all work.
	(b)  Use MATLAB to compute the determinants of the following matrices:  A + B, A - B, A*B, A^T, B^T Note: In MATLAB the transpose of a matrix is denoted with an apostrophe; i.e. A^T is given by the command >> A'
	(c)  Which of the above matrices are NOT invertible?  Explain your reasoning.
	(d)  Now we know the determinants of A and B, but suppose then that we lose our original matrices A and B.  Which of the determinants in part (b) will we still be able to compute, even without having A or B at hand?  Explain your reasoning.

Remark 7.1 The mainusage of determinants in this class relates to the idea of invertibility. When you use MATLAB for that purpose, you have to understand that the programintroduces rounding errors (as you saw in Lab 2).  Therefore, there is a possibilitythat a matrix may appear to have zero determinant and yet be invertible. This only applies to matrices with non-integer entries.  The abovematrices don't fall into this category as all their entries are integers.

Exercise 7.2  In this exercise we are going to work with the following matrix:     Use det() to compute the determinant of N^100.  Do you think that N^100 is invertible?  Also use the command to compute the determinant of N.     Now, using the determinant of N as a known quantity, calculate by hand the determinant of N^100. What do you notice? Hint: look at Remark 7.1 and consider some of the properties of determinants.

§7.2 Eigenvalues

    For the rest of this lab we'll be looking at eigenvalues and eigenvectors of matrices.  The commandthat we will be using here is eig().  We can either useit to compute eigenvalues alone, or with a littlealteration we can get eigenvectors as well.  Let's use it on our twomatrices A and B.

Example 7.2

    Compute the eigenvalues of thematrix B and assign the values to a vector b.

We do this by typing the following

>> b = eig(B)

   b =

      1
       8
       3
       2

    The eigenvalues are 1, 8, 3, 2.  There are four of them because our matrix is 4x4.  Notice also that it is very easy to compute thedeterminant of B.  All we have to do is multiply all the eigenvalues together.  Clearly 48 =1*8*3*2. (Further information about this can be found in your linearalgebra book, Linear Algebra and Its Applications by D. Lay, in chapter5 section 2.)

Exercise 7.3
	(a)  Compute the eigenvalues of the 5x5 Vandermonde matrix V and assign them to a vector v. To enter this matrix into MATLAB use the following command: >> V = vander(1:5)     If you don't know what a Vandermonde matrix is look here.  We strongly encourage you to familiarize yourself with these matrices as they have very nice properties.
	(b)  Determine if V is invertible by looking at the eigenvalues. Explain your reasoning.

    Let's now compute the eigenvaluesand eigenvectors of B in one command.  To do this we type

>> [P,D] = eig(B)

    P =

        1.0000  -0.1980   0.2357    0.9074
       0         0.6931 -0.2357   -0.1815
       0         0.6931  0.9428    0.3630
       0         0       0         0.1089


    D =

        1 0 0 0
        0 8 0 0
        0 0 30
        0 0 0 2

    MATLAB defines the matrix P which has theeigenvectors of B as its columns and the matrix D as a diagonalmatrix with the corresponding eigenvalues along thediagonal.

    An important use of eigenvaluesand eigenvectors is in diagonalizing matrices. You will see why we might want to do that in the next section.  For now,all we want to do is find an invertible matrix Q such that Q*B*Q^-1= diagonal matrix.  But before we do this, we need to make sure thatB is diagonalizable.  In general the way to determining diagonalizability of a matrix is to make sure that itseigenvectors are linearly independent.  There is another way too.  Wealready know the eigenvalues of B so let's putthem to use. B is diagonalizable since all of its eigenvalues are distinct.

Remark 7.2  Thelast statement says that if a matrix has distinct eigenvalues,then it is diagonalizable.  Note that the converse to the precedingstatement is not necessarily true; i.e., if a matrix is diagonalizable, it isnot necessarily true that all its eigenvalues aredistinct.  A matrix can be diagonalizable even if it has repeated eigenvalues: think about the identity matrix (alreadydiagonal) whose eigenvalues are all 1.

    Here is where our two matrices P and D comein. Type the following command:

>> inv(P)*B*P

ans =

    1.0000   -0.0000  -0.0000    0.0000
   0         8.0000   0        -0.0000
   0         0.0000   3.0000    0
   0         0        0         2.0000

What you should realize is that we are using linearly independent eigenvectors(from the matrix P) to diagonalize our matrixB.  The result is a diagonal matrix with eigenvaluesas its diagonal entries.

Remark 7.3 Recallthat the inv()command calculates the inverse of a matrix.  To see that it really workstry the following command:

>> inv(P)*P

Exercise 7.4 Find matrices P and D for our Vandermonde matrix V.  Calculate inv(P)*V*P to check your work.

§7.3Fibonacci Numbers

    The Fibonacci numbers comprise a well-known sequence inmathematics.  The idea is very simple.  You start with two numbers, 1and 1, and get each consecutive term by summing the two previous terms. That is, the third term would be 1+1=2, the fourth term 1+2=3, the fifth term2+3=5, and so on, resulting in

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, . . .

Remark 7.4 To learn more about the sequence, go to this site.  It contains an interesting discussion ofrabbit population growth.  That is the original problem with whichFibonacci concerned himself.

    We are going to use the Fibonacci numbers as a model forour own sequence.  Here it is:

1, 1, 3, 5, 11, 21, 43, ...

Instead of adding two consecutive terms to create the next term, we are goingto use the following formula:

a_n= a_n-1 + 2a_n-2

That is, each term in the sequence is the sum of the previous term and twotimes the term before that.  Let's try to come up with a formula for the n^thterm in our sequence.  Looking at it, it is not that obvious that thereactually exists such a formula.

    Our approach is to start by formulating the problem interms of a system of linear equations:

an+1	=	an+2an-1
an	=	an

where a_n is the n^thterm.  Now, each system of linear equations has its matrix representation.In this case we get

Let's define

We then get the following equation:

f_n= F*f_n-1

Similarly, f_n-1 = F*f_n-2, sothat we can replace f_n-1 with F*f_n-2. Then we can replace f_n-2, and so on.  This will resultin the following formula:

f_n=(F^n)f₀

We assume that a₀ is the first term in the sequence and

    All we have to do now is find the formula for F^n.  The best way to approach this task isthrough diagonalization.  Inorder to do that we first have to determine if F is diagonalizable. Enter F into MATLAB.

Exercise 7.5 Find matrices P and D for our matrix F as described above and explain why F is diagonalizable.

    The above exercise tells us that F = P*D*P^-1. We use this to get the following equation

F^n= [P*D*P^-1]*[P*D*P^-1]*...*[P*D*P^-1] (n times)

which reduces to

F^n= P*(D^n)*P^-1

    All we need at this point is D^n,and since D is diagonal the calculation is very simple.  The lastthing to do is to plug it all back into the original equation and read off theformula.  But before we can do this we have to note that MATLAB likes tonormalize eigenvectors.  In this case it means making the entriesirrational, and hence introducing a possibility for floating pointerrors.  To counteract this we are going to use the following command:

>> [P,D] = eig(F,'nobalance')

Exercise 7.6
	(a)  Include input and output from the above command
	(b)  Use the above matrix P (the one with fractions) to hand calculate the inverse of P.
	(c)  Determine the formula for the n^th term in our sequence, i.e., the formula for an.  (This is a tricky question. Make sure to count the terms correctly.) Use your formula to calculate the 5th, 15th and 20th terms in our sequence.

§7.4 Conclusion

    Even though the process of computing determinants and eigenvalues is quite easy to understand, the complexity ofcalculations can be horrendous.  MATLAB is a perfect tool for this.  There'sonly one caveat: floating-point errors.  However, this obstacle can beovercome if you know they might occur.

---

Last Modified:

03/25/2005