5. Linear Dependence, Column Space, Null Space, and Bases

§5.1 Introduction

    In this lab we will talk about some of the most important concepts in linear algebra: the column and null space of a matrix, linear dependence, and bases of vector spaces.  One cannot overstate the importance of these ideas and a solid grasp of them is essential for anyone interested in studying linear algebra.  Hopefully this lab will reinforce some of the ideas from the lectures and make you feel more confident in working with matrices and bases.

§5.2 Linear Dependence

    Recall that the vectors v1, v2, ..., vn are linearly dependent if there are real constants a1, a2 , ..., an, not all zero, such that

a1v1+ ... +  anvn  = 0

Thus the vectors (1, 0)T, (0, 1)T, (2, 1)T  are linearly dependent, since (2, 1)T - 2(1, 0)T - (0, 1)T = 0.

Exercise 5.1
Include full-sentence response. (a)  For the following collection of vectors, see if you can figure out if the vectors are linearly independent or not.  If they are not, exhibit a linear combination which is zero:

{(1, 5)T, (2, 2)T, (3, -1)T }
Include full-sentence response. (b)  Do the same for the following collection of vectors:

{(6, 0, 3)T, (2, 1, 2)T, (5, 2, 2)T }

    Suppose that the vectors v1, v2, and v3 are linearly dependent.  This means that there are real constants a1, a2, and a3 not all zero such that

a1v1+ a2v2 + a3v3  = 0

If we solve for v1  then we get

v1 = (- a2/ a1 )v2 - (a3/ a1 )v3

For instance, from the example above we have, (2, 1)T  = 2(1, 0)T + (0, 1)T.  So (2, 1)T can be written as a linear combination of the other two vectors, which means that it is in the linear span of (1, 0)T and (0, 1)T. 

It is also true that the vectors (1, 0)T, (0, 1)T, (3, 1)T  are linearly dependent, since (3, 1)T - 3(1, 0)T - (0, 1)T = 0. So we can write (3, 1)T  = 3(1, 0)T + (0, 1)T. In fact, the vectors (1, 0)T, (0, 1)T, (a, 1)T  are linearly dependent, since (a, 1)T - a(1, 0)T - (0, 1)T = 0. So we can write (a, 1)T  = a(1, 0)T + (0, 1)T, where a is any real number. 

Exercise 5.2
Include full-sentence response. (a) Are (1, 0)T, (0, 1)T, (a, b)T linearly independent? If they are, exhibit a linear combination which is zero.
Include full-sentence response. (b) What is the dimension of {(a, b)T : a, b are real}? 
Include full-sentence response. (c)  Based on the previous exercises, what do you think the dimension of Span((1, 0)T, (0, 1)T) is?
Include full-sentence response. (d)  What is the dimension of Span((1, 0)T, (0, 1)T, (2, 1)T )?

    MATLAB has a function called rank() that could help us compute the dimension of spans of vectors.  (The rank of a matrix will be defined in class soon, but for now we are just going to use it to compute dimensions of vector spans.)

Exercise 5.3
Include input and output. (a)  Let

>> A = [0 1 ; 1 0]

That is, form a matrix with the two vectors in Exercise 5.2(a) as the columns. Use MATLAB to compute

>> rank(A)
Include input and output. (b)  Let

>> B = [0 1 2 ; 1 0 1]

That is, form a matrix with the three vectors in Exercise 5.2(b) as the columns.  Compute the rank of B as well.
Include full-sentence response. (c)  What do you notice about the numbers obtained in Exercise 5.2(c) and (d) versus the numbers MATLAB gave you in Exercise 5.3(a) and (b)?
Include full-sentence response. Include input and output. (d)  What is the dimension of Span((1, 3)T, (3, 1)T, (3, 5)T)? Verify this using MATLAB.
Include full-sentence response. (e)  Using what you have learnt above, explain how the dimension of the span of a set of vectors can be used to ascertain whether or not that set is linearly independent. 

§5.3 Column Space and Null Space

    Let A be the matrix [1 2 5 ; 4 5 7 ; 2 3 6].  The column space of A is the linear span of the columns of A; that is, the span of the vectors (1, 4, 2)T, (2, 5, 3)T, (5, 7, 6)T.  Since rank(A) gives the dimension of the span of  the columns of A, it gives the dimension of the column space of A.

    Consider the following matrix 

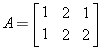
First, let us find the rank of A and a obtain a basis for the column space of A. 

>> A = [1 2 1; 1 2 2];
>> rank(A)

ans =

  2

    Recall that the null space of A is the set Null(A) = {x : Ax = 0}.  MATLAB has a command null(A) that produces a basis for the null space of A.  Simply enter:

>> x = null (A, 'r')

x =

    -2
     1
     0

Remark 5.1  The parameter 'r' above is used so that MATLAB does not orthogonalize the basis; that is, it does not change the vectors in the basis to be of unit length and perpendicular to each other. You will learn about orthogonalization in a few lectures.

    Note that it makes sense that the null space is one dimensional since the rank-nullity theorem states that nullity(A) + rank(A) = dim (R3) = 3

    Now let us check that the vector x really does lie in the null space:

>> A*x

ans =

0
0

    So how do we find a basis for the column space?  As you probably know from lectures and homework, all we have to do is perform row reduction on A and look which columns contain pivots (i.e. leading ones).  Then we simply choose the corresponding columns from the original matrix A .

>> rref(A)

ans =

1   2   0
0   0   1

We see that columns one and three contain pivots.  The first and third columns in A are (1, 1)T, (1, 2)T.  A moment of reflection should convince you that this is indeed a basis for the column space consisting of columns of A.  Note that this result is consistent with our calculations for the rank of A .

 
Exercise 5.4
Include input and output. Include full-sentence response. (a)  Consider the matrix:

Use MATLAB to find a basis for the null space of A and to check that the vectors of this basis are indeed in the null space of A.  What is the dimension of the null space of A?  Include all your input and output in your final lab write up.
Include input and output. Include full-sentence response. (b)  Use MATLAB to find the rank of A.  Does your answer satisfy the conclusion of the Rank-Nullity Theorem? If the rank is less than 4, it means that some columns can be expressed as linear combinations of others. Find one set of such expressions.
Include input and output. Include full-sentence response. (c)  Use MATLAB to find the reduced row echelon form of A and then use it to write down a basis for the column space of A.
Include input and output. Include full-sentence response. (d)  Consider the following set of column vectors:

B = {(1, 1, 1)T, (2, 0, 1)T, (4, 2, 3)T, (-1, 1, 0)T, (1, 3, 2)T}.

Use MATLAB to find the dimension of span(B) and to obtain a basis for span(B) consisting of elements of B.  (Hint: Consider a matrix A whose columns are the vectors of B).
Include full-sentence response. (e)  Can you think of a 2x2 matrix whose null space has the same dimension as its column space?  What about a 3x3 matrix?  Explain your answers.

Last Modified:

09/20/04