3. Matrix Algebra

    The purpose of this lab is to make you feel comfortable using MATLAB to perform various operations with matrices.  As you already know, matrices can be added, subtracted, and multiplied (provided they have appropriate dimensions).  Certain square matrices can also be inverted.  In addition to learning how to use MATLAB to work with matrices, you will also see two applications of matrices to some concrete, real-world problems.  These applications are supposed to be fun, so please pretend as if you enjoy doing them even if you do not to make your TA feel like he or she is making a difference.

§3.1 Addition and Multiplication

    You  have already seen that we can add two matrices of the same dimensions by adding their corresponding entries.  The operator MATLAB uses to add matrices is simply '+', as the next example shows:

Example 3.1  

    Let us first enter some matrices into MATLAB:

>> A = [1, 2, 3, 4; 5, 6, 7, 8]
>> B = [8, 7, 6, 5; 4, 3, 2, 1]

We can add them by typing

>> A+B

ans =

9   9   9   9
9   9   9   9

    As you know, matrix multiplication is defined in a way that may seem strange at first glance.  However, this way of defining matrix multiplication turns out to work to our advantage in the future.  You may have seen some of the motivation for this definition in lecture.  To recap, recall that if we have a matrix A of dimension k x l and a matrix B of dimension l x m, we can multiply them to obtain a k x m matrix AB.  Note that in order to be able to multiply two matrices, the number of columns of the first one must be the same as the number of rows of the second one.  For your convenience here is the definition:

(AB)_ij = ∑ A_inB_nj

Here (AB)_ij represents the ij^th entry of the matrix AB and n runs from 1 to l in the summation.

Example 3.2 

    Enter the following matrices into MATLAB:

>> A = [1, 1; 1, 0]
>> B = [0, 1; 1, 1]

Now multiply them, simply by typing

>> A*B

ans =

1   2
0   1

What happens if we multiply B by A?

>> B*A

ans =

1   0
2   1

When you multiply two matrices A and B, it is not true in general that AB = BA!

 

Exercise 3.1  Can you think of any 2x2 matrices D for which CD = DC for all 2x2 matrices C? Can you list all such matrices D?

    We can do other things with matrices as well. Among things to try are:

>> A-B	(Subtracts two matrices.)
>> 2*A	(Multiplies matrix A by a scalar 2.)
>> A^3	(Raises the matrix A to the third power, i.e., multiplies A by itself three times.)
>> A.*B	(Multiplies the corresponding entries of the matrices together. We will not be using this command very often, but it is nice to know.)
>> rref(A)	(Gives the reduced row echelon form of A.)

where A and B are the same matrices defined in the above example.

 

Exercise 3.2
	(a)  Enter the following matrices into MATLAB and compute the following expression: C = (3A2B - 2A)2
	(b)  Now find the reduced row echelon form of C.  Is C invertible? Explain your answer.
	(c)  Compute C*x and include all your input and output into your final write up.

§3.2 Application: Incidence Matrices

    Consider the following problem: suppose we have six cities with airports, say San Diego, San Francisco, Chicago, New York, Moscow, and Tokyo.  We are interested in counting the number of ways we can travel from one city to another with at most n stopovers.  Suppose for example that there are direct flights from

San Diego to San Francisco
San Francisco to any of the remaining five cities
Chicago to San Francisco, New York, and Moscow
New York to San Diego, San Francisco, Chicago, and Moscow
Moscow to Chicago, New York, and Tokyo
Tokyo to San Francisco, New York, and Moscow

and we want to count the number of ways we can get from San Diego to Moscow with at most 3 stopovers.

    At first glance this problem has little to do with matrices and linear algebra, but it turns out that there is a very easy and elegant way of solving problems of this type using something called incidence matrices.

    The first step is to number our cities in the order they are listed: San Diego will be 1, San Francisco 2, and so on.  Then, let us set up our incidence matrix A by the following rule: if we can get from the i^th city to the j^th city, then the entry A_ij of the matrix will be set to 1.  Otherwise we set that entry to 0.  By convention we will set all of the diagonal entries, A_ii to 0.  Thus we obtain the following matrix A for our situation:

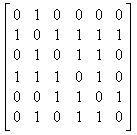
We can now find a useful interpretation for the entries of the matrix A². Take, for example:

(A²)₃₆ = A₃₁A₁₆ + A₃₂A₂₆ + A₃₃A₃₆ + A₃₄A₄₆ + A₃₅A₅₆ + A₃₆A₆₆

Note that any of the terms A_3kA_k6 = 1 if and only if both A_3k and A_k6 equal 1, that is, if and only if we can fly from Chicago to the k^th city and from the k^th city to Tokyo. Thus (A²)₃₆  gives us the number of ways of flying from Chicago to Tokyo with exactly one stopover. Similarly one can show that the number of ways of flying from city i to city j with exactly n stopovers is just (Aⁿ⁺¹)_ij.

Remark 3.1  As you have probably realized, the method discussed above counts silly trips such as San Francisco -> New York -> San Francisco -> New York as a trip with 2 stopovers, so, user beware!

§3.3 Matrix Inversion

    A concept of fundamental importance is that of the inverse of a matrix.  Recall that we define the inverse of an n x n matrix A to be a matrix B such that AB = BA = I, where I is the n x n identity matrix.  Usually the matrix B is denoted by A^-1.  Note that it follows from the definition that B is also an  n x n matrix.

    As we know, every nonzero real number x has an inverse, namely 1/x.  However, this need not be the case with matrices.

    MATLAB has a special command, inv, that finds the inverse of a matrix, if one exists.

    If you want to find an inverse of a square matrix M, simply type

>> inv(M)

Exercise 3.5
	(a)  Try using the inv command to find the inverse of the matrix in the above exercise. Notice the strange output. Include your command and the output in the final write up.
	(b)  Now enter matrix A into MATLAB. >> A = [1, 4; 4, 15] Let us find its inverse: >> B = inv(A) and check that it satisfies the definition. Enter the following commands. >> A*B >> B*A Include your commands and the output they produced in the final write up. Remark 3.2  MATLAB may give you entries such as -0.000 as the result of multiplying the matrices above.  Don't pay too much attention to that.  -0.000 is still 0 for all practical purposes.
	(c)  Enter the following column vector into MATLAB: >> x = [5;10] Now multiply A by x by entering the following command: >> y = A*x As usual, include your input and output in the final write up.
	(d)  Now without entering anything into MATLAB (no cheating!), what do you think will be the result of B*y?  Explain your answer.
	(e)  Check your answer to the above question, by entering the appropriate commands into MATLAB.  Include the input and output in your Word document.

§3.4 Application to Encryption

    In conclusion, we will present a simple method of encrypting a piece of text using matrices and its inverses.

    Any text message, such as, for example, "I LOVE MY TA," can be translated into a string of numbers by agreeing that each letter will correspond to its position in the alphabet, and a blank space will correspond to the number 27.  Thus A corresponds to 1, B corresponds to 2, and M corresponds to 13.  Then the message above can be written as "9 27 12 15 22 5 27 13 25 27 20 1."  If we did this alone, our message would be quite easy to break.  Let us use our sophistication in linear algebra to try to come up with a better encoding procedure.

Let us pick some invertible 4x4 matrix C with integer coefficients. For example let

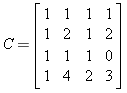
Now to encode our numerical message we simply take the first four numbers in our string and multiply C by it.

>> C*[9;27;12;15]

This gives us the first four numbers of the encoded string:

63 105 48 186

Thus to encode the rest of the message we keep multiplying C by the next four numbers in the original array.

    Now we know how to encode a text message, but it is of little use to us if the party to whom we are sending it cannot decode it.  Thus we must devise a way of decoding an already-encoded message.  That is, given an encoded message we must work in reverse to find the original message.  This is done by applying the inverse of the encoding matrix to the encoded string.

Example 3.3

    Let us decode the encrypted message "42 51 34 81," knowing that it was encrypted using the matrix C.

    We must first find the decoding matrix. This involves finding the inverse of C. Type in:

>> D = inv(C)

Then simply multiply D by the column vector representing the encoded message.

>> D*[42;51;34;81]

ans =

    13
    1
    20
    8

What does that say?

Last Modified:

09/19/04