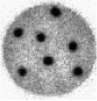
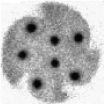
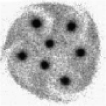
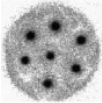
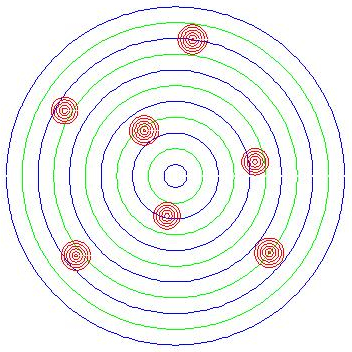
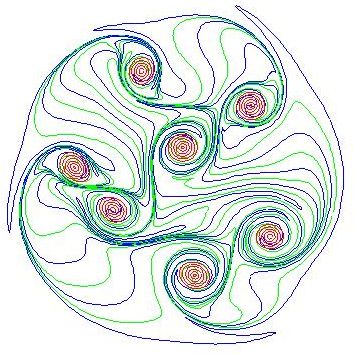
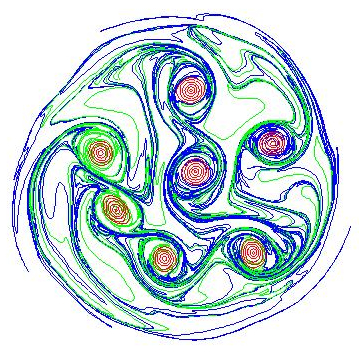
Fully Lagrangian methods for problems in plasma physics: (Collaborator: Professor Robert Krasny, University of Michigan) This numerical method is mesh free. The basic method extends and merges ideas related to numerical Green's functions, fast summation algorithms and dynamic point insertion. The approach has been successfully applied to a wide range of 1D and 2D test problems in electrostatic plasma physics. Below is an example calculation were the methods have been applied to the problem of dynamic crystal formation in magnetic confined plasmas. Figure 1: Penning-Malmberg trap crystal formation. The top row is experimental data taken at the University of California San Diego. The second and third rows are two methods of visualizing the same simulation data. Row two is a visualization of the actual Lagrangian points and row three uses a weighting to a mesh similar to how the data is obtained. From left to right, the panels are in order of increasing time. In addition to working on extending this approach to a wider class of problems, I am currently working on fast summation algorithms for time dependent Green's functions. These methods will allow for accurate mesh free simulations of electromagnetic plasmas as well as wave propagation in other nonlinear materials. This work is supported by the Air Force Office of Scientific Research Back to Andrew J. Christlieb's research page Back to Andrew J. Christlieb's Homepage christlieb@math.msu.edu