Computational Gas Dynamics: (Collaborators: Dr. Spencer Olson NRC-Post. Doc.) In this work we have developed an innovative grid-free approach to Monte Carlo methods for gas dynamics problems. The evolution of the new Boltzmann equation is carried out using operator splitting in time, i.e., we evolve the macro particles, which describe the transport of the distribution function through phase space and then correct the resulting distribution for collisional events using a Monte Carlo method. Novel aspects in this work are that particles are clustered adaptively using octrees at each time step and that macro flow quantities are tracked and updated in the nodes of the tree using grid-free interpolation. 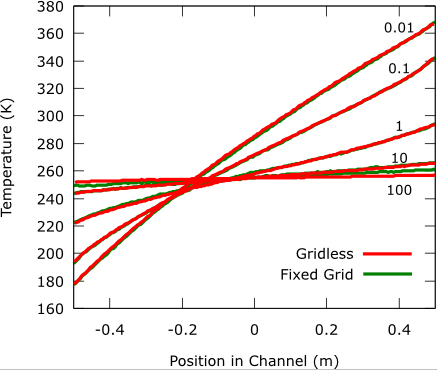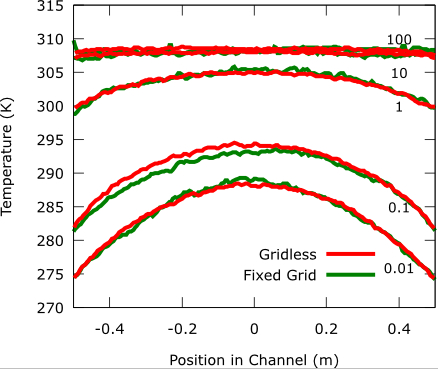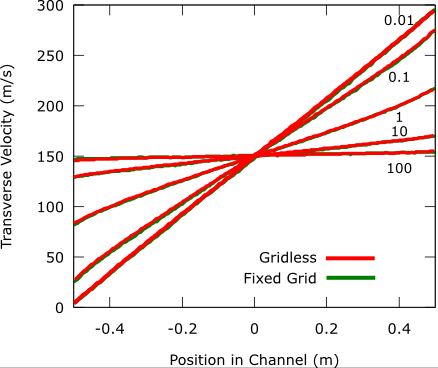The method has been applied to several benchmark problems such as, Couette flow, thermal Couette flow and flow past a lifting body. Couette flow is flow between two parallel infinite moving plates and thermal Couette flow is heat flow between two stationary parallel plates with a large temperature jump between them. The results for Couette and thermal Couette flow are in good agreement with traditional meth based methods, see Figure 1. Figure 1: Simulation results for grid based and grid-free Monte Carlo simulations of thermal and velocity driven Couette flow. The images show results for a range of densities, k_n in { 0.01,0.1, 1, 10,100}. Note that k_n is the mean free path over a characteristic length, as k_n approaches infinity, the density goes to zero. On the far right the plot is of the temperature profile for the thermal Couette flow. The middle and left plots are the temperature and velocity profiles for the velocity driven Couette flow. This work is supported by the Air Force Office of Scientific Research Back to Andrew J. Christlieb's research page Back to Andrew J. Christlieb's Homepage christlieb@math.msu.edu