Coarse Grained Kinetic Models: (Collaborators: Professor James Rossmanith, University of Wisconsin and Professor Peter Smereka, University of Michigan) Simplified models which capture the essential underlying physics are essential for analyzing basic mechanisms. In this work we are interested in studying rarefied gas flows in a thin channel. Here essential implies that, under the right scaling, the solutions of the kinetic model weakly converge to solutions of simplified models. For collisonless flow, the flow reduces to a set of fluid equations with a viscous force to account for wall interactions. 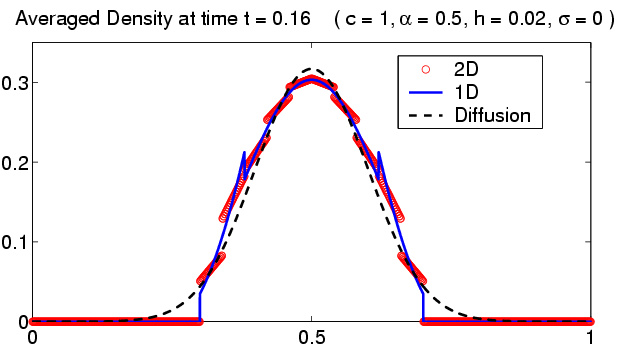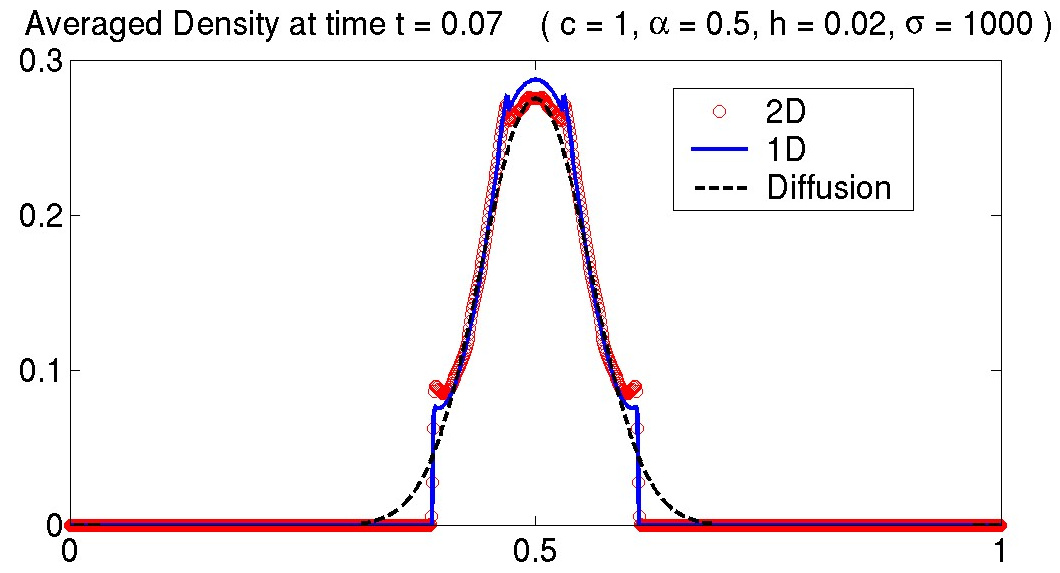As a first step towards the development of a reduced physical model for flow in a thin channel, we start by considering a simplified kinetic model, the Broadwell model with appropriate boundary conditions. We derive two 1D models for gas transport in a thin channel by depth averaging the model and making use of Taylor expansions. In the limit of no inter-particle collisions, the 1D model reduces to the well known telegraph equation. In the case of collisional flow, the 1D model is a system of three first-order hyperbolic PDEs. Both 1D models have been validated by comparison with numerical solutions of the 2D Broadwell system. Figure 1 shows the results of the 1D models compared to the 2D depth averaged model and the solution to the diffusion equation for the initial conditions of a top-hat density profile. The 1D models are in good agreement with the 2D system and both the 2D and 1D models converge to the solution of the diffusion equation for long time scales. Figure 1: Density versus position: (a) collisionless case and (b) collisional case. The open circles are the depth averaged model 2D results, the solid line is the 1D model and the dashed line is the diffusion equation result. Back to Andrew J. Christlieb's research page Back to Andrew J. Christlieb's Homepage christlieb@math.msu.edu