My research interests include
- Ordinary and Partial Differential Equations,
- Dynamical Systems,
- Pattern Formation,
with an emphasis on dynamics of pattern forming systems arising in biology, chemistry and physics. To mathematically illustrate the formation mechanisms of patterns, I am concerned mainly with the existence of solutions representing patterns, their defects and their interfaces, together with their qualitative properties, such as linear and nonlinear stability/instability, bifurcations, etc.
Patterns in nature

A: Meteorite ALH8400I(NASA); B: Diatoms(R. Lowe); C: Sand Ridges; D: Stripes on a Zebra; E: Desert of Baja California(A. Franco); F: A tree
Useful Links
|
Amphiphilic Morphorlogy
Amphiphilies, molecules containing both hydrophilic and hydrophobic components, self-assemble into a cornucopia of phase-separated, nano-scaled morphologies, including distinct co-dimensional patterns and their defects. In the biological setting, such structures arise as ubiquitous plasma membranes, playing critical roles in protein synthesis, membrane signaling and trafficking and pathways to primitive cell division. Within the context of synthetic chemistry, amphiphilic copolymers materials also received extensive attention, for their wide application in pharmaceutics, emulsion stabilization, detergent production and energy conversion devices.
The functionalized Cahn-Hilliard (FCH) free energy has been proposed as a bilayer
model which allows competition between morphologies with distinct co- dimensions and
between morphologies of the same co-dimension but with distinct composition. In fact,
the FCH free energy is a special case of the model proposed by Tubner and Stray and later
Gompper and Schick, based on small-angle X-ray scattering (SAXS) data of micro-emulsions
of soapy-oil in water. More specifically, the FCH free energy for the vector volume
fraction function u of the N amphiphilic phases in a single solvent phase,
takes the form
The pearling bifurcation from bilayers into higher co-dim morphologies is a periodic, high- frequency, in-plane modulation of the bilayer thickness. For the sFCH equation, we employ spatial dynamics and a center manifold reduction to reduce the stationary sFCH to an 8th order ODE. A normal form analysis shows that the reduced system admits a degenerate 1:1 resonance, from which we deduce that the onset of the pearling bifurcation coincides with the creation of a two-parameter family of pearled equilibria.
Pearling


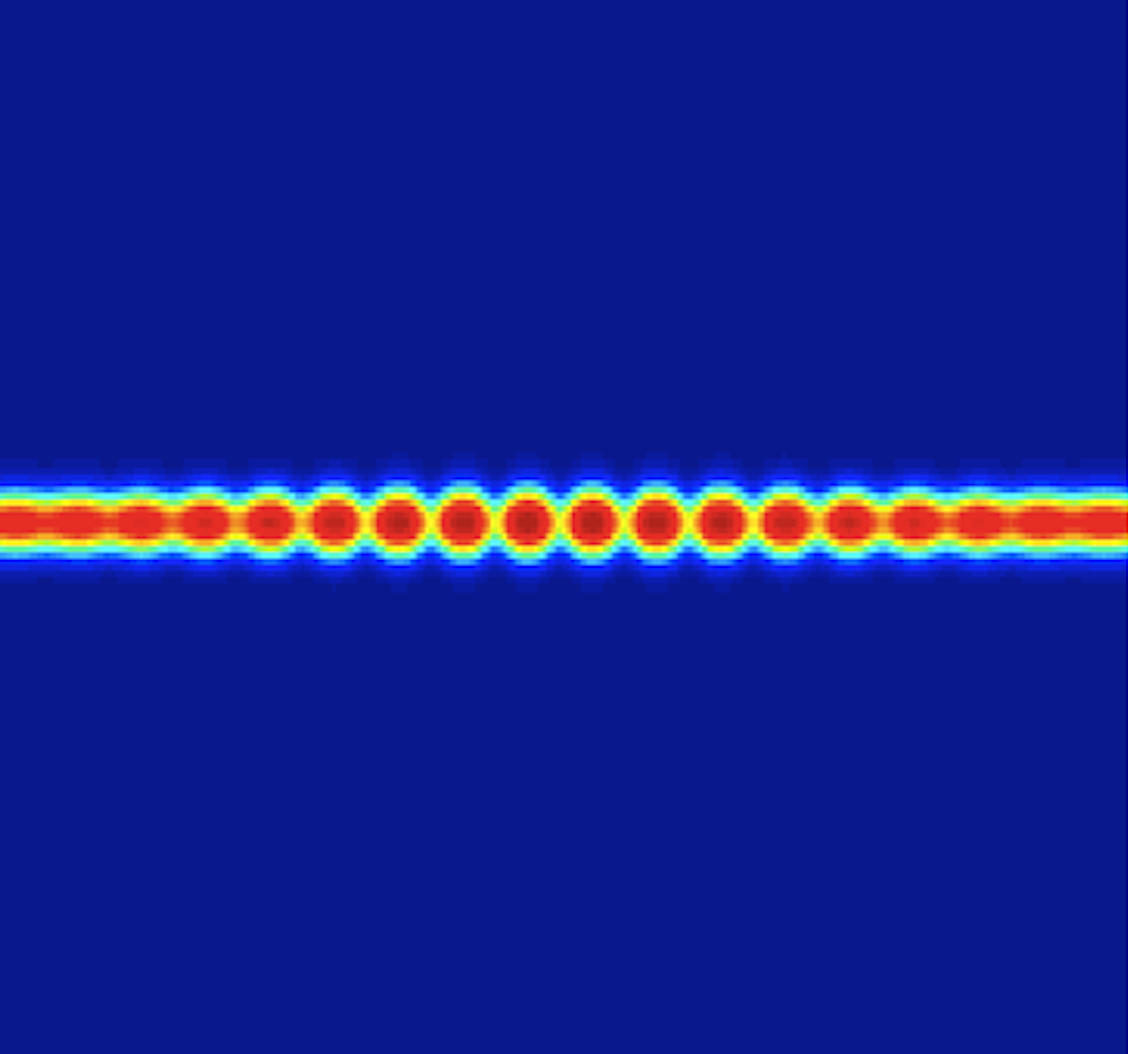
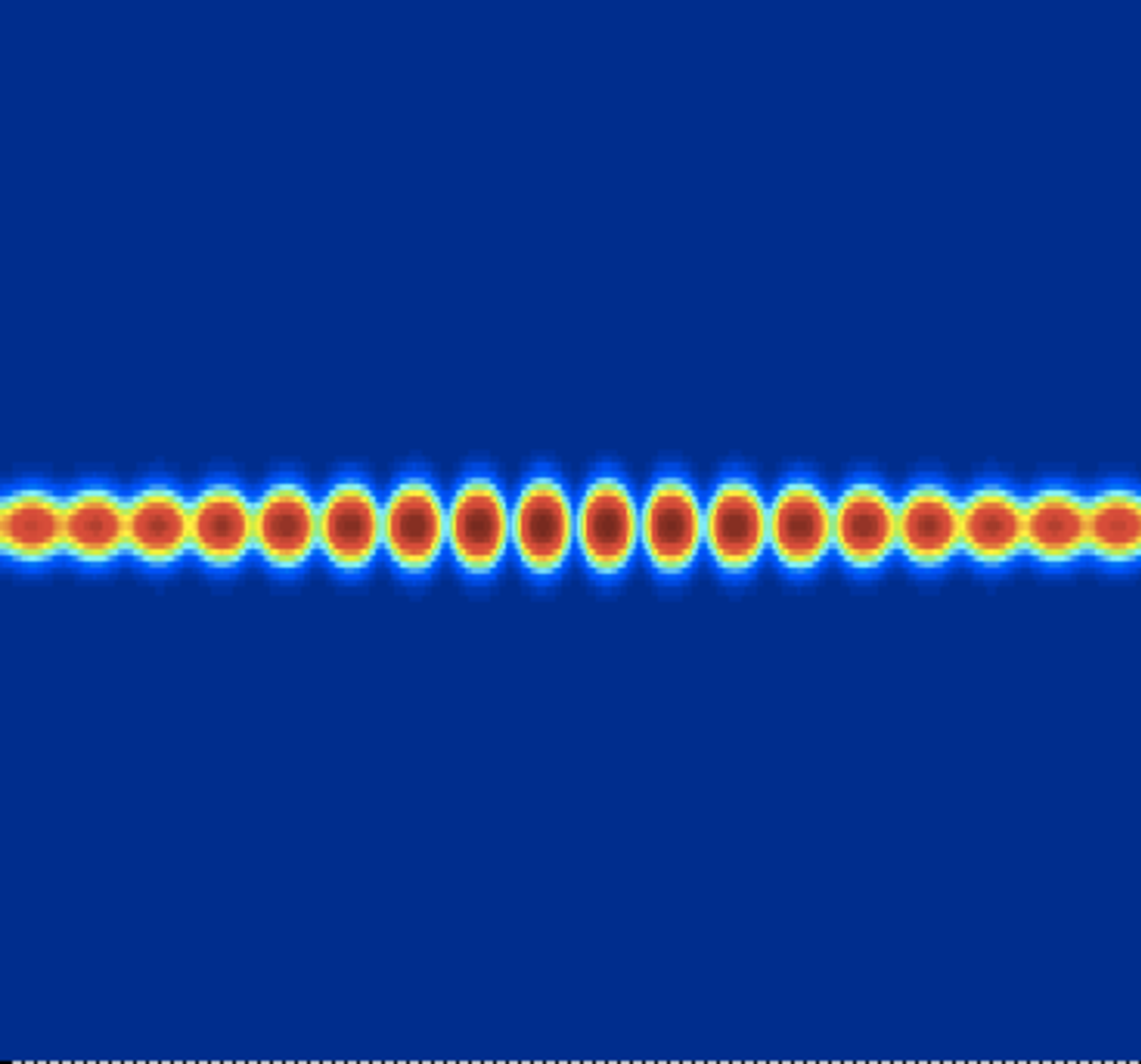


Fig by Keith Promislow
We show that the set of quasi-bilayers is almost invariant under the H-1 gradient flow of mFCH:
the evolution of a quasi-bilayer is a quasi-bilayer plus small perturbations. More specifically,
in the slow time scale τ = ε2t, the evolution reduces to an interface-area-preserving
Willmore flow of the interface Γ(τ),
where Vn and H are the normal velocity and extended curvature of the interface,
M is a constant associated to the unperturbed homoclinic and ΠΓ is a curvature-weighted projection.
More importantly, the background state m(τ) is slaved to the Willmore flow and
the Willmore flow admits the circular bilayer with its mean curvature H0 = a0 as an equilibrium.
Geometric evolution
Turing patterns
We investigate dynamics near Turing patterns in reaction-diffusion systems posed on the real line. Linear analysis predicts diffusive decay of small perturbations. We construct a normal form coordinate system near such Turing patterns which exhibits an approximate discrete conservation law. The key ingredients to the normal form is a conjugation of the reaction-diffusion system on the real line to a lattice dynamical system. At each lattice site, we decompose perturbations into neutral phase shifts and normal decaying components. As an application of our normal form construction, we prove nonlinear stability of Turing patterns with respect to small perturbations in L1 ∩ L∞, with sharp rates, recovering and slightly improving on results in earlier works by G. Schneider and K. Zumbrun.
Diffusive Decay

Grain boundaries arise as stationary interfaces between roll solutions of different orientations. Our analysis shows that such stationary interfaces exist near onset of instability for arbitrary angle between the roll solutions. This extends prior work where the analysis was restricted to large angles, that is, weak bending near the grain boundary. The main new difficulty stems from possible interactions of the primary modes with other resonant modes. We generalize the normal form analysis in an earlier work by Arnd Scheel and Mariana Haragus and develop a singular perturbation approach to treat resonances.
Compatible roll solutions(8Π-y-period)

Saddle searching
Computational simulations nowadays can accurately describe systems of hundreds of atoms, in sizes relevant to experimental conditions, thanks to the development of the density function theory. However, its current deficiency in time scale greatly limits its capacity: Any chemical reaction taking longer than micro-seconds is out of the reach of regular molecular dynamics. To capture long time scale chemical evolutions, a powerful alternative tool is the harmonic transition state theory (HTST), in which the reaction rate can be captured by low-energy saddles on the potential energy surface (PES). Since the computation cost of locating saddles is the highest part in HTST, there have been extensive research on developing efficient saddle searching methods. As part of this collective effort, we proposed two methods: the Basin constrained κ-dimer method and the biased gradient squared descent (BGSD) method. There are two major issues in developing and improving saddle searching methods: one is the redundancy of repeatedly finding the same saddles; or one may find saddles that do not contribute to transitions from the prescribed initial reactant.
The original dimer method intrinsically admits the later deficiency: Local ridges that the dimer method follows generically diverge from the separatrix of the initial state, that is, the true ridge, leading the search into adjacent states. We introduced the concept of the isopotential curvature κ which enjoys the valuable property that the κ = 0 surface and the true ridge tend to intersect only at saddles. The κ-dimer method restrains the dimer method to the κ = 0 surface, greatly reducing the chance of flowing to a disconnected saddle point, and thus significantly enhancing the efficiency.
κ-dimer
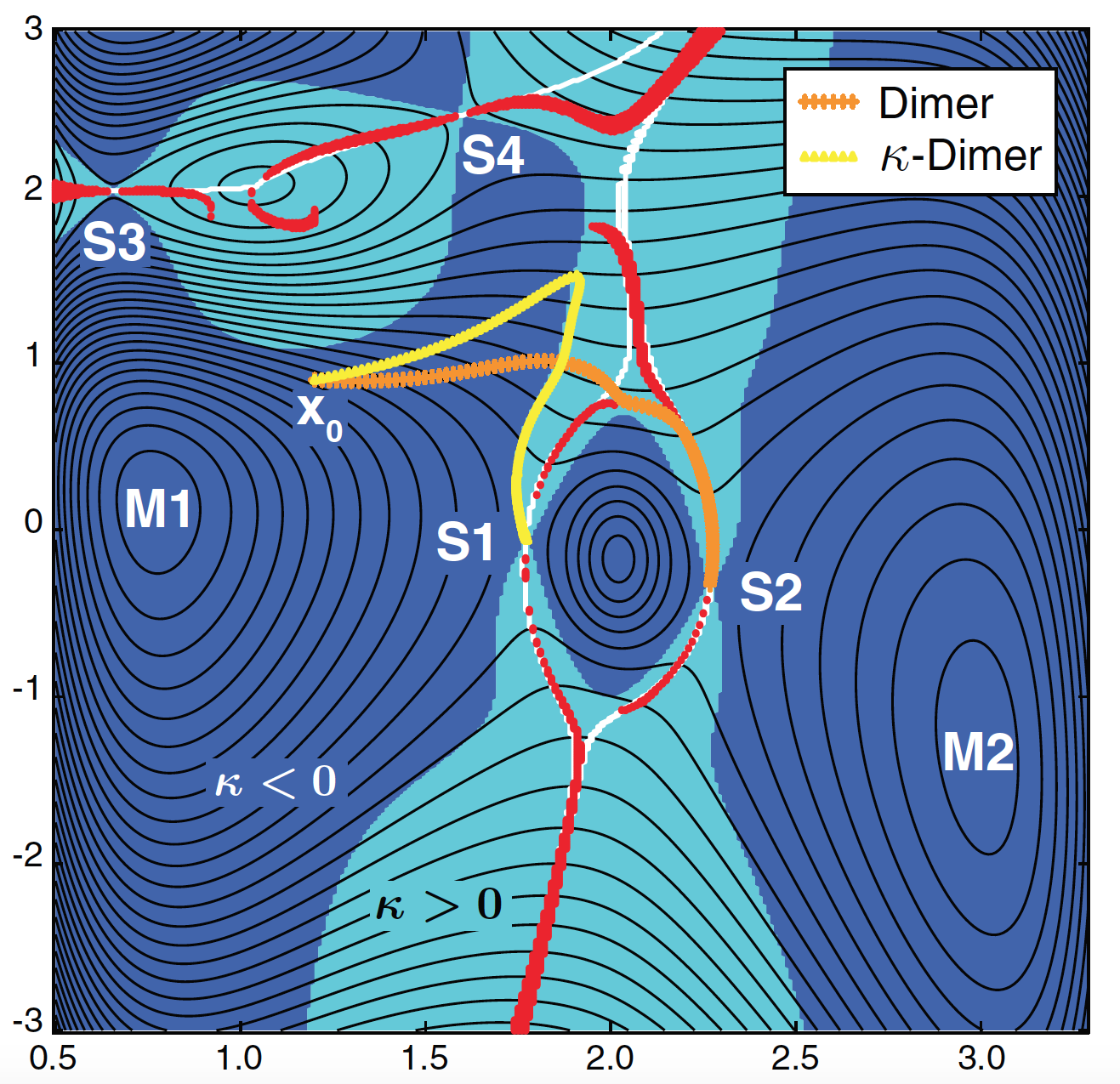
Fig by Penghao Xiao
Motivated by the FCH model, we also developed a novel biased gradient squared descent (BGSD)
method: Given a PES, V (r), its gradient square
can be biased to a chosen level-set β
with the biased strength α via
The saddle points of V are the minima of H, and the BGSD considers a pure gradient descent on H. By tuning parameters, BGSD can find saddles of V within an energy range of V near β, circumventing the calculation of minimal eigenvectors. The merit of BGSD also lies in its extended ability to find any critical point on the PES. Overall, the BGSD method, with the distinctive ability of targeting saddles with specific energy values, is competitive with the dimer method in terms of the saddle-searching efficiency.
BGSD
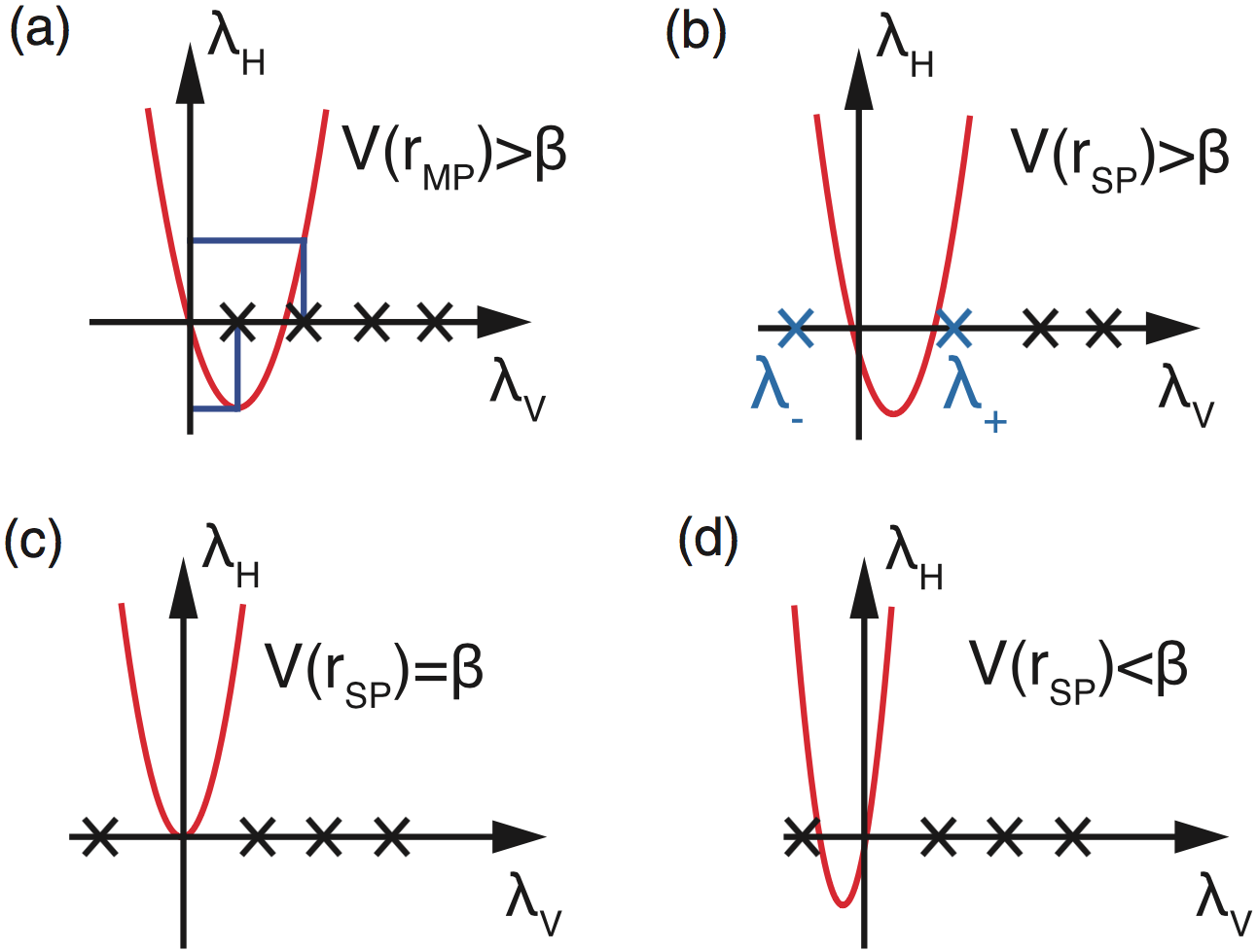
Fig by J. Duncan