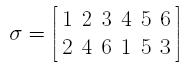I will not collect homework (except problems marked Hand In), but the next daily quiz will be based on it. You may also hand in problems marked Extra Credit, preferably within a week of the HW date. Each problem you give up on is a lost opportunity to learn: only look at the solution after a serious effort.
I will give an extra point to the first person pointing out a significant typo or other error on this page. Corrections and recent revisions are in red. Future assignments, which are tentative and may be revised, are marked in gray.
On this page, I will denote the binomial coefficient (n choose k) as (n | k), and the multi-set number (n multi-choose k) as ((n | k)). Use the standard vertical notation on your papers. Also, the set of the first k positive integers is denoted [k] = {1,2,...,k}.
- 1/8: Twelvefold Way (1).
Reading:- The Twelvefold Way: Notes 1/8 - 1/13, [S] p. 79−81.
- Deletion Transform: Notes 1/8, Wikipedia.
- General Review: Old Notes from Math 481, especially Notes 9/6 on multi-choose numbers ((n | k)).
- A shirt has 6 positions for buttons, which you sew on according to each rule below. For each problem, find the correct entry of the Twelvefold Way table which counts the given type of button arrangements. Evaluate this number to solve the problem. =
- You have a supply of 3 kinds of buttons (Black, White, Red), and you sew on any 6 of them. Example: (B,W,W,W,B,B) where R does not appear.
- Same as (a), but every color must appear. Example: (B,W,W,W,R,B).
- Same as (a), but some positions might be left empty (−). Example: (B,−,W,W,B,−).
- You have 9 distinct buttons (1,2,...,9), and you sew on any 6 of them. Example: (8,4,5,3,1,9).
- The 6 positions already have 6 distinct buttons (1,2,...,6), and you snip them off and rearrange them. Example: Rearrange to (3,1,5,6,4,2).
- You sew on 3 identical Black buttons, leaving 3 positions empty (−). Example: (B,−,B,B,−,−).
- Same as (f), but you may sew several buttons (or none) onto each position: Example: (B,−,BB,−,−,−).
- You sew on 10 Black buttons, allowing several at each position, but no positions empty. Example: (BBB,B,BB,BB,B,B).
- For each of the following entries in the Twelvefold Way, compute the equivalent of Pascal's Triangle for 5 rows and columns. Start by using the definition of each number to find obvious values at the boundaries of the triangle; then use the given recurrence to compute the rest of the values. Check your work with the explicit, non-recursive formula for one sample value.
- Entry #3: compute surj(k,n) for n ≤ k ≤ 5. Start with surj(k,1) and surj(k,k), which are easy to compute from the definition (i.e. counting functions, not using the PIE formula). Check your work against the PIE formula for surj(5,3).
- Entry #4: compute ((n | k)) for n,k ≤ 5 (a square of values rather than a triangle). Start with ((n | 0)) and ((1 | k)), which are obvious from the definition (and also from the explicit formula). Check your work against the explicit formula for ((5 | 3)).
- Extra Credit: You should notice a very, very close relationship between your numbers in (b) for ((n | k)) and the usual Pascal's Triangle for (n | k). Explain how and why this happens. Is there any relation between the numbers in (a) and the usual Pascal Triangle?
- Entry #6 in the Twelvefold Way counts arrangements of k identical balls into n marked bins with no bin empty, given by ((n | k−n)) = (k−1 | n−1). For this problem only, denote this number by a(k,n).
Problem: Use a transformation to find and prove a Pascal's Triangle type recurrence for a(k,n), similar to those for entries #3,4,5. Make a table showing your transformation for a(5,3).
Hints:- Transform each arrangement of balls by removing one ball from the nth basket. The resulting arrangements are of two types, counted by smaller numbers of the same kind. Show that the transformation is reversible (give the inverse transformation).
- For the example of a(5,3), make a table with one column being all arrangements of 5 identical balls in 3 bins, with no bin empty: (•••,•,•), (••,••,•), (••,•,••), etc. Next to each, put the transformed arrangement in the second or third column, depending on which of the two types it is.
- Match shirt-button problems to Twelvefold Way entries.
-
3 kinds of buttons, sew any 6 of them onto the 6 positions. A choice of buttons corresponds to entry #1, a function f : [6]→{B,W,R}, where each position i is taken to its button-color f(i). The example (B,W,W,W,B,B) corresponds to f with f(1) = B, f(2) = W, f(3) = W, f(4) = W, f(5) = B, f(6) = B. The number of such f is nk = 36.
-
3 kinds of buttons, sew on any 6 of them so that every color appears. Entry #3, functions f : [6]→{B,W,R} where all 3 outputs appear, meaning f is surjective. The number of such f is surj(6,3) = 36 − (3 | 1) 26 + (3 | 2) 16.
-
Give each position one of 3 kinds of buttons or leave empty, which is like a 4th color denoted by −. Entry #1: f : [6]→{B,W,R,−}. The number is 46.
- 9 distinct buttons (1,2,...,9), sew on any 6 of them. Entry #2, functions f : [6]→[9] with each output appearing at most once, meaning f is injective. The number is 96 = (9)(8)...(4).
-
6 distinct buttons (1,2,...,6) are rearranged into new positions. This is a function f : [6]→[6], where the button originally at i gets new position f(i). This function must be both surjective and injective (i.e. bijective) since each position gets one and only one button. This is counted either by entry #2, giving 66 = 6! ; or by entry #3, giving surj(6,6) = 66 − (6 | 1)56 + (6 | 2)46 − (6 | 3)36 + (6 | 4)26 − (6 | 5).
These two expressions look very different, but they must give the same number, since f : [6]→[6] is injective if and only if it is surjective (this is known as the Pigeonhole Principle). Try them on Wolfram Alpha, entering (n | k) as binom(n,k), and nk as n^k. Indeed, they are both 720.
-
Sew on 3 Black buttons, leaving 3 positions empty (−). An arrangement corresponds to entry #5, classes of injective functions f : [3]→[6], where it does not matter which input goes to a given output. Thus, we may picture indistinguishable [3] as three identical balls or buttons {•,•,•} tossed into 6 labeled bins or positions, with at most one in each bin. The example: (B,−,B,B,−,−) corresponds to the three values f(1) = f(•) = 1, f(2) = f(•) = 3, f(3) = f(•) = 4. The number of such f is (n | k) = (6 | 3) = (6)(5)(4) / 3! .
-
Same as (e) allowing several buttons at each position. Entry #4, functions f : {•,•,•}→[6] with no restriction. The number is ((6 | 3)) = (6)(7)(8) / 3! .
-
Sew on 10 Black buttons, allowing several at each position, but no positions empty. Entry #6, f : {•,•,•,•,•,•,•,•,•,•}→[6] with every output appearing, meaning f is surjective. The number is ((6 | 10−6)) = (9 | 5) = (9 | 4) = (9)(8)(7)(6) / 4! .
- For (a), see here in the Online Encyclopedia of Integer Sequences, where the table of surj(k,n) is written row-by-row in a single sequence, surj(1,1), surj(2,1), surj(2,2), surj(3,1),...
For (b), each 45-degree diagonal of the square of ((n | k))'s is a row of the ordinary Pascal triangle. Why on earth is that??
- Find a Pascal-type recurrence for a(k,n) = ((n | k−n)) = (k−1 | n−1), which counts arrangements of k identical balls in n marked bins, with no bin empty.
The Tranformation Principle says that if there is a reversible transformation (a one-to-one correspondence, an invertible mapping, a bijection) between all objects of one type and all objects of another, then there is the same number of objects of each type. In our case, we wish to transform an arrangement of type a(k,n) into a smaller arrangement of similar type.
Transform each arrangement of balls by removing one ball from the nth bin. If this empties the nth bin, we drop this bin and get k−1 balls in n−1 bins with no bin empty, of type a(k−1, n−1). We can reconstruct the original arrangement by restoring the nth bin with a single ball.
If the transformation does not empty the nth bin, we get k−1 balls in n bins with no bin empty, of type a(k−1, n). We can reconstruct the original arrangement by tossing one more ball in the nth bin.
Thus the arrangements of type a(k,n) are reversibly transformed into all those of the types (k−1, n−1) and a(k−1, n), so the Transformation Principle gives:
a(k,n) = a(k−1, n−1) + a(k−1, n).
Example a(5,3) = a(4,2) + a(4,3). The transformation takes any 5 balls in 3 non-empty bins and removes one ball from the third bin, giving either 4 balls in 2 non-empty bins if the third bin is emptied, or otherwise 4 balls in 3 non-empty bins. This is reversed by restoring one more ball to the third bin.
a(5,3) a(4,2) a(4,3) •••|•|• •••|• ••|••|• ••|•• ••|•|•• ••|•|• •|•••|• •|••• •|••|•• •|••|• •|•|••• •|•|••
- 1/10: Twelvefold Way (2).
Reading- Notes 1/8 - 1/13.
- Stirling set partition numbers {k | n} : [HHM] p. 231−233.
- Partition numbers pn(k): [HHM] p. 218−220.
- For the last column of the Twelvefold Way (#3,6,9,12), evaluate each entry for (k,n) = (4,2) by writing out all the objects being counted.
Hints:- Entry #3 counts all surjective functions, in which both possible outputs {1,2} actually appear. The other entries count some of these functions as the same, if you can get one from the other by permuting the 4 inputs or the 2 outputs (switching 1↔2).
- Write each function f : [4]→[2] by listing its outputs: f = (f(1), f(2), f(3), f(4)). For example, write the function f(1) = 2, f(2) = 2, f(3) = 1, f(4) = 2 as (2,2,1,2). In this list notation, permuting the inputs means reordering the list; permuting the outputs means switching 1↔2 in each entry of the list.
- Alternatively, write f as an arrangement of balls {1,2,3,4} inside 2 output bins. For example, write the above function f(1) = 2, f(2) = 2, f(3) = 1, f(4) = 2 as 3|124. In this bin notation, permuting the inputs means replacing each ball-number with a permuted number; permuting the outputs means switching the two bins.
- For each problem, find the entry of the Twelvefold Way table which counts the given type of arrangements. Evaluate the answer if there is a known formula.
- Ways for three candidates (A,B,C) to split 100 votes. Example: A gets 38 votes, B gets 0 votes, C gets 62 votes.
- Same as (a), but we record only the vote-counts, not linking them the names of the candidates . Example: Winner gets 62 votes, second place gets 38 votes, third place gets 0 votes. (Vote ties are also possible.)
- Same as (b), but assume each candidate gets at least 1 vote. Example: Winner 62, second place 30, third place 8.
- Ways for 6 nations (A,B,C,D,E,F) to split into three hostile alliances, so that no nation can belong to more than one.. Example: A,C,F form an alliance, B forms an alliance by itself, and D,E form an alliance. (No alliance can be empty.)
- Same as (d), but with any number of alliances. Examples: everyone is in one big alliance; or, each nation forms an alliance by itself.
- Partitions
- Entry #10 counts partitions: arrangements of k identical balls into n exchangeable bins, with the answer denoted by p≤n(k). Since the balls are identical, we only record how many in each bin; and since the bins can be rearranged, we always put the fullest bin first, then the second-fullest bin, etc. For example, the arrangement of balls •••|•|• is denoted (3,1,1), and p≤3(5) = 5 counts the partitions (5,0,0), (4,1,0), (3,2,0), (3,1,1), (2,2,1).
- As with other entries of the table, I will try a transformation to get a Pascal's Triangle type recurrence for p≤n(k). Given a partition (a1,...,an) with a1 ≥ ··· ≥ an ≥ 0 and a1 + ··· + an = k, either we have an = 0, in which case we can drop an and get the partition (a1,...,an-1) of type p≤n-1(k); or we have an > 0, and we can subtract 1 from an to get the partition (a1,...,an-1, an–1) of type p≤n(k–1).
- This transformation can obviously be reversed, so we seem to have:
p≤n(k) ?=? p≤n–1(k) + p≤n(k–1).
- Dismayingly, this equation is false, as you can see by evaluating p≤2(3) = 2, p≤1(3) = 1, p≤2(2) = 2, with 2 ≠ 1 + 2, This illustrates why we need complete rigor in mathematics: the above argument is not precise enough, neglects a subtle point, and leads to a false result.
- Since the equation is false, there must be a step of false reasoning in the proof. Find it!
Hint: Just apply the "proof" to the counter-example. Make a table of the transformation for p≤2(3) ?=? p≤1(3) + p≤2(2), and you will see immediately where the argument is wrong. Try to explain why the obvious reverse transformation is not a true inverse mapping: what does it lack? - Extra Credit: Find a correct Pascal's Triangle type recurrence for p≤n(k).
- From the Twelvefold Way.
Entry #3. There are surj(4,2) = 14 surjective functions f : [4]→[2]. Writing as f = (f(1),..., f(4)), they are:
(1,1,1,2) (1,1,2,1) (1,2,1,1) (2,1,1,1) (1,1,2,2) (1,2,1,2) (1,2,2,1)
(2,2,2,1) (2,2,1,2) (2,1,2,2) (1,2,2,2) (2,2,1,1) (2,1,2,1) (2,1,1,2).
Alternatively, write f as input balls {1,2,3,4} in 2 output bins:
123|4 124|3 134|2 234|1 12|34 13|24 14|23
4|123 3|124 2|134 1|234 34|12 24|13 23|14.
Entry #6. Two of the above functions count as the same if you can get one from the other by rearranging the inputs (entries in the list), for example (1,1,1,2) = (1,1,2,1). There are ((2 | 4–2)) = 3 distinct surjective functions (i.e. 3 symmetry classes of functions):
(1,1,1,2) (1,1,2,2) (1,2,2,2)
Alternatively, write f : {•,•,•,•} → [2] as 4 input balls in 2 output bins:
•••|• ••|•• •|•••
Another alternative: write the number of balls in each bin (the multiplicity):
3+1 2+2 1+3.
Entry #9. The count for this entry is given by Stirling partition numbers, whose standard vertical notation is given in the Twelvefold Way table. Here I will use a non-standard horizontal notation {k | n} for these numbers, just as I write (n | k) for choose numbers.
Two functions from entry #3 count as the same if you can get one from the other by switching the outputs {1,2}, for example (1,1,1,2) = (2,2,2,1). The count is given by the Stirling number {4 | 2} = 7. distinct surjective functions:
(1,1,1,2) (1,1,2,1) (1,2,1,1) (2,1,1,1) (1,1,2,2) (1,2,1,2) (1,2,2,1).
Alternatively, write a function f : [4]→{•,•} as input balls {1,2,3,4} in 2 output bins, remembering that switching bins gives an equivalent function:
123|4 124|3 134|2 234|1 12|34 13|24 23|14
Entry #12: Two functions count the same if you can get one from the other by a combination of the above two equivalences. Threre are p2(4) = 2 distinct surjective functions:
(1,1,1,2) (1,1,2,2)
Alternatively, write a function f : {•,•,•,•}→{•,•} as 4 input balls in 2 output bins, remembering that switching bins gives the same function.
•••|• ••|••
Another alternative: write the number of balls in each bin (the multiplicity):
3+1 2+2.
Match word problems to the Twelvefold Way.
-
Three candidates (A,B,C) split 100 votes. Entry #4: 100 identical votes into 3 bins A,B,C. Answer ((3 | 100)).
-
Entry #10: 100 identical votes into 3 exchangeable bins. Answer: p≤3(100), which has no simple formula.
-
Entry #12: 100 identical votes into 3 exchangeable non-empty bins. Answer: p3(100), which has no simple formula.
-
Nations (A,B,C,D,E,F) split into three exclusive non-empty alliances are like 6 marked balls put into 3 non-empty, exchangeable bins. Entry #9:
{6 | 3} = 1⁄3! ( 36 – (3 | 1) 26 + (3 | 2) 16 ).
-
Nations (A,B,C,D,E,F) to split into any number of exclusive non-empty alliances. Entry #7: {6 | 1} + {6 | 2} + ··· + {6 | 6}. This is also the Bell number B(6), at the bottom of the Twelvefold Way.
-
To analyze the false equation p≤2(3) ?=? p≤1(3) + p≤2(2), write the partitions of type p≤2(3) as (a1, a2) with a1 ≥ a2 and a1 + a2 = 3. If a2 = 0, the transformation drops it to give the partition (a1) of type p≤1(3); if a2 > 0, the transformation subtracts 1 from it to give the partition (a1, a2 – 1) of type p≤2(2). The table is:
p≤2(3) p≤1(3) p≤2(2) (3,0) (3) (2,1) (2,0) ?? (1,1) Clearly the transformation is not fully reversible: the reverse rule will take every output of the transformation back to the input it came from, but this rule does not work on every entry in the output columns. The reverse rule for the second column takes (a1) back to (a1, 0) = (a1, a2); and for the third column, it should take (b1, b2) = (a1, a2 – 1) back to (b1, b2 + 1) = (a1, a2), meaning (1,1) goes back to (1,2), which is not a valid input.
Thus, the reverse transformation is not defined on the desired set of outputs, and the original transformation is a one-to-one (injective) mapping, but not an onto (surjective) mapping. This will happen in every case with n > 1, so in fact we get the inequality p≤n(k) < p≤n–1(k) + p≤n(k–1).
- 1/13: Other sequences
Reading:- Notes 1/8 - 1/13
- Stirling cycle numbers: Notes 1/13, [HHM] p. 227−230.
- Fibonacci numbers: Wikipedia
- Catalan numbers: Wikipedia, 481 Notes 10/2.
- Tree counting: [HHM] p. 31−32, 43−47, 481 Graph Notes II.7 (Cayley's Theorem).
- Stirling cycle numbers
- Write all the permutations counted by the cycle number [4 | 2] = 11, in both cycle and two-line notation.
- Write the table of the transformation for [4 | 2] = [3 | 1] + 3 [3 | 2].
- Let an be the number of sets S ⊂ [n] which do not contain any two consecutive numbers i, i+1. For example, a4 = 8 counts the sets:
S = {}, {1}, {2}, {3}, {4}, {1,3}, {1,4}, {2,4}.
A set like S = {1,3,4} is not counted, since it contains 3,4.
Problem: Use a transformation to find and prove a recurrence for an, and show it equals one of the types of numbers on the Twelvefold Way handout. -
An unlabeled ordered tree is a schematic family tree starting from an ancestor node at the top,
with child nodes attached below it with the eldest at left, then possible grandchild nodes below them, and so on.
For example, the unlabeled ordered trees with 4 nodes are:
The difference between the third and fourth trees is whether the grandchild belongs to the older or the younger child. Let on be the number of ordered trees with n nodes, so that the above example counts o4 = 5.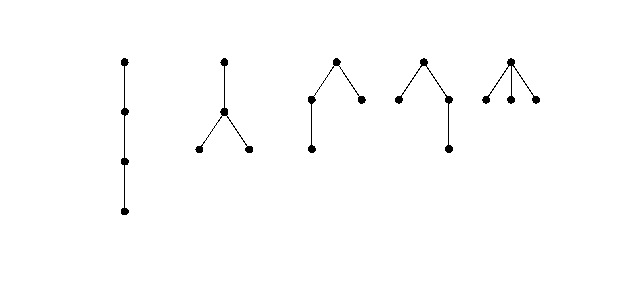
Problem: Use a transformation to find and prove a recurrence for on, and show it equals one of the types of numbers on the Twelvefold Way handout.
Hint: Decompose a tree into a pair of trees by disconnecting the oldest child, and making it the ancestor of its own tree. For each possible size of the new trees, the number of such pairs is a product of two smaller oj's. - Extra Credit: [W] Ch 1, Ex 21(a), p 28: Differentiating eex.
-
The transformation table for the Stirling cycle number identity [4 | 2] = [3 | 1] + 3 [3 | 2] is:
[4 | 2]
[3 | 1]
3 [3 | 2]
(1)(234)
2 , (1)(23)
(1)(243)
3 , (1)(23)
(2)(134)
1 , (2)(13)
(2)(143)
3 , (2)(13)
(3)(124)
1 , (3)(12)
(3)(142)
2 , (3)(12)
(4)(123)
(123)
(4)(132)
(132)
(12)(34)
3 , (12)(3)
(13)(24)
2 , (13)(2)
(14)(23)
1 , (1)(23)
Note that (1)(432) = (1)(243) and (12)(34) = (12)(43), etc., so there are no more permutations to list in the first column. Also, the third column contains every possible combination of a number 1 ≤ j ≤ 3 and a permutation τ of type [3 | 2].
- Deletion transform.
A set of type an is S ⊂ [n] containing no consecutive numbers. In case n ∉ S, transform S to S' = S ⊂ [n–1], a set of type an−1. In case n ∈ S, we must have n–1 ∉ S (otherwise S would contain consecutive n–1, n). Transform S by removing n, getting S' = S\{n} ⊂ [n–2] of type an–2. This transformation is reversible, so we get an = an–1 + an–2, the same recurrence as for Fibonacci numbers Fn. Also, the initial values are a0 = F2 = 1 and a1 = F3 = 2, so thereafter we continue to get an = Fn+2.
- Left-right decomposition transform.
Let on count unlabeled n-node ordered trees.
If we transform such a tree T by disconnecting the oldest (leftmost) child, we get a pair of trees (T1, T2), where T1 is the tree starting from the oldest child,
and T2 is what remains of the original tree.
Also, any pair (T1, T2) can be re-connected to restore T.
If we assume T1 has i nodes and T2 has n – i nodes,
then the number of possible (T1, T2) is oion–i. Summing over all possiblilities for i gives:
on = o1on–1 + o2on–2 + o3on–3 + ... + on–1o1.
If we define cn = on+1, this means:
cn = on+1 = o1on + o2on–1 + o3on–2 + ... + ono1 = c0cn–1 + c1cn–2 + c3cn–3 + ... + cn–1c0 ,
which is precisely the same recurrence as for the Catalan numbers Cn. Also we have the same initial value c0 = o1 = 1 = C0. The same recurrence starting from the same initial value will produce the same numbers: cn = Cn. That is, on = cn–1 = Cn–1.
- 1/15: Review Method of Generating Functions
Reading:- Notes 1/15.
- [HHM] Ch 2.6 p. 164−175.
- 481 HW 9/18−9/25. Dice-throws are discussed in HW 9/23 #1 and 9/25 #3.
- Starting with the definition of the multi-choose number ((n | k)), use the Method of Generating Functions to derive an explicit formula for ((n | k)), different from the bins-and-beans formula ((n | k)) = (k+n−1 | k).
- Step 0: Specify a sequence. Fix n to be constant, and consider the sequence ak = ((n | k)), so that the generating function is:
f(x) = ∑k≥0 akxk = ((n | 0)) + ((n | 1))x + ((n | 2))x2 + ... - Step 1: Using combinatorial properties of {ak}, find a simple formula for the generating function f(x). In this case, we will use the Product Principle for choosing M to get a product formula for f(x).
The multiplicity transform (see 481 Notes 9/6) writes a multi-set by listing how many of each kind. For example, fixing n = 5 kinds, the multiset M = {1,1,1,3,4,4,5} is represented as (3,0,1,2,1), since it has 3 ones, 0 twos, 1 three, 2 fours, 1 five.
This leads to an algorithm for constructing all the multisets M, for arbitrary size k:(choose M from n kinds, any size) ⇔ (0 ones or 1 ones or 2 ones or …) and (0 twos or 1 twos or 2 twos or …) and … and (0 n's or 1 n's or 2 n's or …). Problem: Translate this algorithm into an algebraic formula using the logic-to-algebra chart in today's Notes.
Hint: Choosing mulitplicity j of any kind increases the total size of M by j, so this choice should be translated into xj. Since the logical expression is infinte, the algebraic expression will involve infinte series. Replace these with a simple finite expression, using the Known Series formulas. - Step 2: Use function theory (algebra, calculus) to find the Taylor series of f(x), giving an explicit formula for the coefficients ak. In this case, you can use Taylor's Formula ak = f(k)(0)⁄k!, where f(k)(x) means the kth derivative of f(x). (This formula is always valid, but hardly ever useful, because the derivates get too complicated. In this case, they are manageable.)
- Step 0: Specify a sequence. Fix n to be constant, and consider the sequence ak = ((n | k)), so that the generating function is:
- We have three kinds of coins: one-euro, gold two-euro, and silver two-euro.
Question: How many ways to make a handful of 20 euros from these three kinds of coins?
For example, one way is: 6 one-euros, 3 gold two-euros, and 4 silver two-euros.
Use the Method of Generating Functions to solve this problem.
Hints:- Step 0: Replace one of the numbers in the problem with k, getting a natural sequence of problems a0, a1, a2,..., one of which is the orginal problem.
- Step 1: Use the Product Principle for choosing a handful of coins (with any value), then translate logic to algebra. Note that a one-euro coin translates to x1, but a two-euro coin adds 2 to the value of the handful, so it translates to x2.
- Step 2: Use the identity: 1⁄(1−x) = (1+x) ⋅ 1⁄(1−x2) . This will allow you to write f(x) as a polynomial times a negative-power binomial from the Known Series. Partial fraction decomposition is possible, but not advisable in this case.
- We have the same three kinds of coins as in Prob. 2, but now we lay them out in ordered rows, rather than unordered handfuls.
- Question: How many ways to make a row of 14 coins with value 20 euros? For example, denoting the coins as 1,2g,2s, one possible row is:
(2g,1,1,1,2s,1,1,2g,2s,2s,1,2g,1,1). Use the Method of Generating Functions to solve this problem.
Hints:- Step 0: Replace one of the numbers in the problem with k. Replace the number which makes the most natural generalization of the original problem, changing the underlying structure as little as possible.
- Step 1: Product Principle again, but now with 14 successive choices of coin, rather than just 3 choices about how many of each.
- Step 2: Binomial Theorem.
- Extra Credit: How many ways to make a row of any length with value 20 euros? For example, the shortest row has 10 coins, a mixture of 2g and 2s; and the longest row has 20 coins, all 1's.
Use the Method of Generating Functions to solve this problem.
Hints:- Step 1: The choice algorithm uses the Sum Principle as well as the Product Principal: split into cases, depending on the length of the row.
- Step 2: Partial fractions.
- Question: How many ways to make a row of 14 coins with value 20 euros? For example, denoting the coins as 1,2g,2s, one possible row is:
- A Generating Function formula for multi-choose numbers ak = ((n | k)).
Step 1:Translating the choice algorithm into algebra according to the chart:
Step 2:f(x) = (x0 + x1 + x2 + ...) ⋅ (x0 + x1 + x2 + ...) ⋅ ... ⋅ (x0 + x1 + x2 + ...) The infinite series in parentheses is a geometric series, which by the Known Series is 1⁄(1−x). Thus f(x) = 1⁄(1−x)n.
= (1 + x + x2 + ⋅⋅⋅)n.Taking derivatives of f(x) = (1−x)−n, mindful of the Chain Rule:
f '(x) = (−n)(1−x)−n−1(−1) = n(1−x)−n−1, Now Taylor's Formula gives:f ''(x) = n(−n−1)(1−x)−n−2(−1) = n(n+1)(1−x)−n−2,
⋮
f(k)(x) = n(n+1)(n+2)...(n+k−1)(1−x)−n−kak = f(k)(0)⁄k! = n(n+1)(n+2)...(n+k−1)(1−0)−n−k⁄k! Now using the rising-power notation nk = n(n+1)(n+2)...(n+k−1), which is pronounced "n to the k rising", we get:
= n(n+1)(n+2)...(n+k−1)⁄k!((n | k)) = ak = nk / k! .
This is of course equivalent to ((n | k)) = (k+n−1 | k), but this form is neater, and nicely analogous to (n | k) = nk / k! .
- Counting handfuls of three kinds of euro coins (one, gold two, silver two) worth a total of 20 euros. Handfuls are multi-sets, so this will be similar to Prob. 1.
Step 0: Let ak be the number of handfuls of the three kinds of coins worth a total of k euros. This is the natural generalization of the problem, rather than changing the kinds of coins.
Step 1:
Because a handful is unordered, all that matters is how many of each kind of coin. The choice algorithm is:
Step 2:(choose a handful, any value) ⇔ (0 ones or 1 ones or 2 ones or …) and (0 golds or 1 golds or 2 golds or …) and (0 silvers or 1 silvers or 2 silvers or …).
Translating into algebra, replacing one by x1, gold and silver by x2:
f(x) = (x0 + x1 + x2 + ...) ⋅ (x0 + x2 + x4 + ...) ⋅ (x0 + x2 + x4 + ...) Using z = x2 in the known geometric series 1⁄(1−z) = 1 + z + z2 + …, we find 1 + x2 + x4 + … = 1⁄(1−x2). Hence:
= (1 + x + x2 + …)(1 + x2 + x4 + …)2.f(x) = 1⁄(1−x)(1−x2)2 The denominator is factorable as (1−x)3 (1+x)2, so a partial fraction expansion would be of the form:
Follow-up: It is wise to check this with Wolfram Alpha (which I should have done originally): the power series of f(x) = 1⁄(1−x)(1−x2) is indeed:f(x) = A⁄(1−x) + B⁄(1−x)2 + C⁄(1−x)3 + D⁄(1+x) + E⁄(1+x)2 . Yuck! Not worth the trouble! Hard to compute, and the resulting formula would be a mess, anyway.
A much better trick is the following: since 1−x2 = (1−x)(1+x), we can substitute 1⁄(1−x) = (1+x) ⋅ 1⁄(1−x2) to consolidate the denominator as a power of a single binomial factor:f(x) = (1+x)⁄(1−x2) ⋅ 1⁄(1−x2)2 = (1+x) ⋅ 1⁄(1−x2)3
Knowing the negative-power binomial series 1⁄(1−x2)3 = ∑k≥0 ((3 | k)) x2k, we find:
f(x) = (1+x) ⋅ ∑k≥0 ((3 | k)) x2k = ∑k≥0 ((3 | k)) x2k + ∑k≥0 ((3 | k)) x2k+1
a2k = a2k+1 = ((3 | k)) = ½(k+2)(k+1).
The answer to our original problem is therefore: a20 = a2(10) = ((3 | 10)) = ½(12)(11) = a2k = 66.
f(x) = 1 + x + 3x2 + 3x3 + 6x4 + 6x5 + 10x6 + 10x7 + 15x8 + 15x9 + 21x10
+ 21x11 + 28x12 + 28x13 + 36x14 + 36x5 + 45x16 + 45x17 + 55x18 + 55x19 + 66x20 + ...This can be explained combinatorially as follows: to get a total value of 20 euros, we must have an even number of one-euro coins. Grouping the one-euros into pairs, we can think of this as 3 kinds of 2-euro coins: one-euro pair, gold two-euro, silver two-euro. The ways to choose a multi-set of 10 of these 2 kinds is ((3 | 10)). This is much clearer in retrospect, once the Generating Function Method has given us the answer.
- (a) Counting rows of 14 coins of three kinds (one, gold two, silver two) worth a total of 20 euros. This will be similar to rolling a sequence of dice.
Step 0: Let ak be the number of rows of 14 of the three kinds of coins worth a total of k. This is the natural, minimal generalization of the problem, rather than changing the length of a row or the kinds of coins. It would be possible to replace 14 with k, but this would not yield a tractable generating function.
Step 1:
Because a row is ordered, we must choose the 14 coins one by one. The choice algorithm is:
Step 2:(choose 14 coins, any total value) ⇔ (coin 1 is one or gold or silver) and (coin 2 is one or gold or silver) and … and (coin 14 is one or gold or silver)
Translating into algebra:
f(x) = (x1 + x2 + x2) ⋅ … ⋅ (x1 + x2 + x2) = (x+2x2)14.
Factoring and applying the Binomial Theorem:
Follow-up: This can be explained combinatorially as follows: to get a total value of 20 from 14 coins, we must have 8 ones and 6 twos. Choose 6 of the 14 positions for the twos, giving (14 | 6) possibliities; then choose whether each two is a silver or a gold, giving 26 possibilities. Again, this is clear once we know the answer!f(x) = x14 (1+2x)14 = x14 ∑k=014 (14 | k) (2x)k = ∑k=014 (14 | k) 2k xk+14.
- 1/17: Generating functions and recurrences (1)
Reading:- Notes 1/15: Memorize the Known Series
- Notes 1/17: The machinery of enumeration for the Fibonacci numbers
- [W] Ch 1, p. 1−11.
- [HHM] Ch 2.6 p. 177−183.
- 481 HW 9/27−9/30
- Generating function warmups: [W] Ch 1, p 24, Ex #1(b,g), 3(b,e,h).
- Problem: For any number r, find an explicit formula for the summation:
ak = r + 2r2 + 3r3 + … + krk. - Find a simple formula for the Taylor series: ∑k≥0 rkxk. Hint: Known series, with a substitution.
- Find a simple formula for the Taylor series: ∑k≥0 k rkxk. Hint: Perform a suitable operation on the formula from part (a).
- Step 1: For the sequence ak above, find a simple formula for the generating function f(x) = ∑k≥0 akxk.
Hint: Start with the recurrence ak = ak−1 + k rk. - Step 2: Find the Taylor series of the formula from part (c).
Hint: You will need a partial fraction decomposition of the form:A⁄(1−x) + B⁄(1−rx) + C⁄(1−rx)2.
-
Goal: Approximate the numbers ak defined by the recurrence:
ak = ak−1 + ak−3 for k ≥ 3, with initial values a0 = a1 = a2 = 1.- Step 1: Find a simple formula for the generating function: f(x) = ∑k≥0 akxk.
- Preliminaries to Step 2. The denominator p(x) = x3 + x − 1 has a real root
α and two complex conjugate roots β, γ.
Compute α to 5 decimal places.
Also, letting |z| denote the length or modulus of a complex number, show that:
|α| < 1 < |β| = |γ|. Hint: Ask Wolfram Alpha, or use Newton's Method with a spreadsheet or calculator. - Note that the above polynomial can be written as:
p(x) = x3 + x − 1 = (x−α) (x−β) (x−γ). The quotient q(x) = p(x) / (x−α) can thus be written as:q(x) = (x−β) (x−γ) = x2 − (β+γ)x + βγ. Problem: Perform long division of polynomials to get a different expression for q(x) = (x3 + x − 1) / (x−α), writing the coefficients in terms of α. (Compute with α just as with any real number, like π or √2, keeping in mind that α3 + α − 1 = 0 by definition.) Then determine β+γ and βγ in terms of α. -
Step 2: To get the dominant term in the Taylor series of f(x), find the coefficient A in the partial fraction decomposition:
f(x) = A⁄(1 − x/α) + B⁄(1 − x/β) + C⁄(1 − x/γ). Your answer for A should be in terms of α, which was computed in part (b). - Explain why we have a good approximation ak ≅ A⁄αk for large k. Apply this approximation to a10, and compare to the exact value.
- Extra Credit:
- For the Fibonacci sequence Fk, peform Step 1 of the Method in a different way, not using the recurrence formula. Start from the combinatorial model:
Fk = #{ (a1,...,ar) with r≥1 and a1+...+ar = k−1 and ai = 1 or 2 }. Then use the Product and Sum Principles: write a choice algorithm split into cases depending on the value of r, with each case consisting of a sequence of independent choices. - From Prob 3 above, consider the sequence defined by the recurrence ak = ak−1 + ak−3 for k ≥ 3,
starting from a0 = a1 = a2 = 1.
This has generating function f(x) =
1 ⁄(1 − x − x3).
Reverse the analysis of part (a) above to get a combinatorial model for an: that is, a set of simple combinatorial objects which are counted by an.
- For the Fibonacci sequence Fk, peform Step 1 of the Method in a different way, not using the recurrence formula. Start from the combinatorial model:
- See [W] p 197.
- Summing the series ak = r + 2r2 + 3r3 + ... + krk.
-
Substituting z = rx into the Known Series
1⁄(1−z)
= ∑k≥0 zk gives:
∑k≥0 rkxk = ∑k≥0 (rx)k = 1⁄(1−rx). -
Taking the left side of the above equation, then
differentiating and multiplying by x gives:
gives:
x d⁄dx ∑k≥0 rkxk = x ∑k≥0 rk kxk−1 = ∑k≥0 krkxk. Applying the same operations to the right side of the equation:x d⁄dx 1⁄(1−rx) = rx⁄(1−rx)2. Hence:∑k≥0 krkxk = rx⁄(1−rx)2. - Now we consider f(x) = ∑k≥0 akxk,
for ak = ∑j=1k j rj
Step 1: We can define ak by the recurrence for ak = ak−1 + krk for k≥1, starting from a0 = 0. Substituting this into the generating function:f(x) = ∑k≥0 akxk = a0 + ∑k≥1 (ak−1 + krk)xk . Distrubuting the summation and factoring out x, then substituting the definition of f(x) and the series formula from part (b):f(x) = 0 + ∑k≥1 ak−1xk + ∑k≥1 krkxk
= x∑k≥1 ak−1xk−1 + ∑k≥1 krkxk
= x f(x) + rx⁄(1−rx)2.f(x) = x f(x) + rx⁄(1−rx)2. Solving:f(x) = rx⁄(1−x)(1−rx)2. - Step 2: We want to write f(x) in terms of Known Series, in this case as a partial fraction decomposition:
f(x) = rx⁄(1−x)(1−rx)2 = A⁄(1−x) + B⁄(1−rx) + C⁄(1−rx)2. Since the right side has a known Taylor series (substituting z = rx into the Known Series), this will immediately allow us to write:ak = A + Brk + C ((2 | k)) rk. All we need is to determine the constants A,B,C.-
Clearing denominators in the equation for f(x) gives:
rx = A(1−rx)2 + B(1−x)(1−rx) + C(1−x). This is an identity of quadratic polynomial functions, which should hold for all values of x. We could expand the right side and equate the 3 coefficients on the two sides, giving 3 linear equations in the 3 variables A,B,C, which we could then solve by Gaussian elimination. -
A quicker way is as follows. Substituting x = 1 makes two of the terms vanish:
r(1) = A(1−r)2 + B(0) + C(0), so A = r⁄(r−1)2. Similarly, substituting x = 1⁄r gives C = r⁄(r−1). Substituting one more value, say x = −1, gives an equation for the remaining unknown B:r(−1) = A(1+r)2 + B(2)(1+r) + C(2), which we can solve to get: B = − r2⁄(r−1)2. - The laziest way is just to ask Wolfram Alpha for: partial fractions rx/((1-x)(1-rx)^2). This is fine, so long as you know how the computer gets its answer: don't use it as a magic oracle of mathematical wisdom.
ak = A + Brk + C ((2 | k)) rk. This is messy, but can't be simplified.
= (krk+2 − (k+1)rk+1 + r) ⁄(r−1)2Follow-up: Compare this to the sum of a finite geometric series:
1 + r + r2 + ... + rk = (rk+1−1) ⁄(r−1) . Once we have our formula, we can prove it very easily, by multiplying out (1−r)2 (r + 2r2 + ... + krk), and finding we can cancel all the terms except for krk+2 − (k+1)rk+1 + r.
We can also check the formula in special cases. For example, for r = 0 we get ak = 0, as expected. For r = 1, we get ak = 1 + 2 + ... + k. Our formula is not valid at r = 1 since the denominator vanishes. However, we can apply L'Hopital's Rule twice as r → 1, giving:ak = (k(k+2)(k+1) − (k+1)(k+1)k) ⁄2 = ½k(k+1), which is indeed correct. -
Clearing denominators in the equation for f(x) gives:
-
Substituting z = rx into the Known Series
1⁄(1−z)
= ∑k≥0 zk gives:
- Solve the recurrence:
ak = ak−1 + ak−3 for k ≥ 3,
starting from a0 = a1 = a2 = 1.
- Step 1: We again substitute the recurrence into the generating function, to get an algebraic equation involving f(x):
f(x) = ∑k≥0 akxk = a0 + a1x + a2x2 + ∑k≥3 (ak−1 + ak−3)xk Substituting a0 = a1 = 1 and simplifying, we find that the function f(x) satisfies:
= 1 + x + x2 + ∑k≥3 ak−1xk + ∑k≥3 ak−3xk
= 1 + x + x2 + x ∑k≥3 ak−1xk−1 + x3 ∑k≥3 ak−3xk−3
= 1 + x + x2 + x (f(x) − a0 − a1x) + x3 f(x)f(x) = 1 + x f(x) + x3 f(x) . Solving, we get our simple formula:f(x) = 1 ⁄(1 − x −x3).
This is almost (but not quite!) the same as the Fibonacci generating function x⁄(1 − x −x2) , which is derived in exactly the same way.
- For the polynomial p(x) = x3 + x − 1, Wolfram Alpha gives the roots:
α ≅ 0.68233, β ≅ −0.34116 + 1.16154 i, γ ≅ −0.34116 − 1.16154 i The real root is clearly the smallest, with |α| = α < 1, and the pair of complex conjugate roots are larger, with |β| = |γ| ≅ 1.2 > 1. - Long division of the form: x−α ) x3 + 0x2 + x − 1
gives the quotient q(x) = x2 + αx + (α2+1), with remainder
α3 + α − 1 = 0.
Comparing this with q(x) = x2 − (β+γ)x + βγ, we find:
β + γ = −α and βγ = α2 + 1. - Step 2: To get an explicit formula for ak, we would determine the coefficients of the partial fraction expansion:
f(x) = 1 ⁄(1 − x −x3) = A⁄(1−x/α) + B⁄(1−x/β) + C⁄(1−x/γ). Such an expression exists because the left and right sides have the same horizontal and vertical asymptotes: y = 0 and x = α, β, γ. Note that substituting z = x/α, x/β, x/γ into the geometric series for 1⁄(1−z) this will immediately give the Taylor series of f(x), so thatak = A⁄αk + B⁄βk + C⁄γk . However, we would like a neater formula, depending only on the real root α. In part (d), we will show that there is a good approximation ak ≅ A⁄αk , dropping the last two terms of the above exact formula. To get this, we only need to find A.Writing the denominator as 1−x− x3 = −(x−α)(x−β)(x−γ) and clearing denominators, we get:
1 = Aα(x−β)(x−γ) + Bβ(x−α)(x−γ) + Cγ(x−α)(x−β), and substituting x = α gives A = 1⁄α(α−β)(α−γ), which we can simplify by part (c) as:
A = 1⁄α(α2 − (β+γ)x + βγ) = 1⁄α(3α2+1) . Hence we have the approximation:
ak ≅ 1⁄(3α2+1)αk+1 ,
- Follow-up:
Why is the above approximation very accurate for large k? Because
1⁄|α|
≅ 1.47, whereas
1⁄|β|
=
1⁄|γ|
≅ 0.83. Hence the A term of the exact formula grows exponentially, whereas the
B and C terms shrink exponentially to zero.
Applying the above approximation to k = 10, we get a10 ≅ 27.95, whereas the exact value is 28. Not bad!
Let us compare ak to the Fibonacci sequence Fk. We can see from the recurrence that ak grows more slowly than Fk : the reproduction is more delayed in ak. And indeed, ak ≅ const × 1.47k, whereas we previously showed the approximation Fk ≅ const × 1.62k.
- Step 1: We again substitute the recurrence into the generating function, to get an algebraic equation involving f(x):
- 1/22: Generating functions and recurrences (2)
Reading:- [W] Ch 1, p. 11−21.
- Notes 1/17.
Generating Functions imply:
- Asymptotic approximations, by taking the dominant term corresponding to the smallest vertical asymptote.
- Recurrences, by clearing denominators and equating coefficients.
- In class, we found the generating function of the Stirling partition numbers {n | k} for fixed k ≥ 1:
fk(x) = ∑n≥k {n | k} xn = xk ⁄(1 − x)(1−2x)…(1−kx) .
Work out the constants A1,..., Ak in the partial fraction decomposition:
fk(x) = A1 ⁄(1 − x) + A2 ⁄(1 − 2x) + ... + Ak ⁄(1 − kx) .
- A set enumeration problem: [W] Ch 1, p 26, Ex #12.
Let a(n,k) be the number of k-element subsets S ⊂ [n] which do not contain any two consecutive numbers i, i+1.
For example, a(6,3} = 4 counts the sets S = {1,3,5}, {1,3,6}, {1,4,6}, {2,4,6}; but a set like S = {1,3,4} is not counted, since it contains 3,4.
- Find the Pascal-triangle type recurrence satisfied by these numbers
- Take a suitable generating function, and find an explicit formula for a(n,k).
Hint: You must decide whether to hold n or k fixed, taking the other as the summation variable. Compare with [W] p. 14−16. - Comparing with HW 1/13 #2, give a formula for the Fibonacci numbers Fk in terms of the a(n,k)'s found in part (b).
- In today's Quiz, we showed that the recurrence sequence ak = 2ak−1 + 1 for k≥1, with a0 = 2, has generating function
f(x) = (2−x)⁄(1−2x)(1−x) . By decomposing the generating function into partial fractions, we obtained the explicit formula ak = 3(2k) − 1.- We can also go backwards: knowing the generating function, we can deduce the recurrence formula. Partially clear the denominator to get the equation:
f(x) (1−2x) = (2−x)⁄(1−x) = 1 + 1⁄(1−x) . Expand into Taylor series on both sides, and equate the coefficient of xk on the left with the corresponding coefficient on the right. Show that this recovers the original recurrence formula: that is, the generating function "knows" the recurrence for the coefficients. - Repeat part (a), clearing denominators in different ways, so the left side is f(x)(1−x), or f(x)(1−2x)(1−x). Expanding both sides into Taylor series, derive new, unexpected recurrences for ak.
- We can also go backwards: knowing the generating function, we can deduce the recurrence formula. Partially clear the denominator to get the equation:
- Extra Credit: From HW 1/17 #3, consider the sequence defined by the recurrence ak = ak−1 + ak−3 for k ≥ 3,
starting from a0 = a1 = a2 = 1.
This has generating function: f(x) =
1⁄(1 − x − x3) .
Reverse the analysis of HW 1/17 #4(a): starting with the generating function, find a combinatorial model for an, meaning a set of simple combinatorial objects which are counted by ak.
- See [W] p 18, where our fk(x) is called Bk(x). Or see [HHM] Ch 2.8.3 p. 234−235.
- Set enumeration. The coefficients which we denote a(n,k) are called f(n,k) by Wilf. For (a), (b) see [W] Solutions p 199, Ch 1 #12. For (c), see p 200, #13.
- Generating functions ⇒ recurrences.
- We expand the equation:
f(x) (1−2x) = (2−x)⁄(1−x) = 1 + 1⁄(1−x) Since the Taylor coefficients of any function are unique, each coefficient on the left must equal the corresponding coefficient on the right, and we obtain: a0 = 2, a1 − 2a0 = 1, a2 − 2a1 = 1, etc., and in general: ak − 2ak−1 = 1. That is, ak = 2ak−1 + 1 for k≥1, which is the original recurrence.a0 + a1x + a2x2 + a3x3 + .... = 1 + 1 + x + x2 + x3 + ...
−2a0x − 2a1x2 − 2a2x3 − ... - Clearing denominators in the second way:
f(x) (1−x) = (2−x)⁄(1−2x) = 1⁄2 + (3⁄2 ) 1⁄(1−2x) Equating coefficients, we find ak − ak−1 = 3(2k−1) for k≥1. Unravelling this recurrence, we find, for k≥1:a0 + a1x + a2x2 + a3x3 + .... = 1⁄2 + 3⁄2 + 3⁄2 (2x) + 3⁄2 (22x2) + 3⁄2 (23x3) + ...
−a0x − a1x2 − a2x3 − ...ak = 5 + 3(2) + 3(22) + 3(23) + ... + 3(2k−1). Clearing denominators in the third way:
f(x) (1 − 3x + 2x2) = f(x) (1−x)(1−2x) = 2 − x That is, ak − 3ak−1 + 2ak−2 = 0 for k≥2, or: ak = 3ak−1 − 2ak−2 for k≥2. We didn't expect that!a0 + a1x + a2x2 + a3x3 + .... = 2 − x + 0x2 + 0x3 + ...
−3a0x − 3a1x2 − 3a2x3 − ...
2a0x2 + 2a1x3 + ...
- We expand the equation:
- 1/24: Formal power series
Reading: Notes 1/24 and [W] Ch 2, pp 30-39.
HW:- Reciprocals in R[[x]].
To compute 1⁄f(x) , you can work coefficient by coefficient using the recursive formula in the Lemma above.
Alternatively, if a0 = 1, substitute the series z = −∑n≥1 anxn into the geometric series
1⁄(1−z)
= 1 + z + z2 + ⋯ .
- [W] Ch 2 p 65 Ex #1. Hint: For part (a), start by expanding cos(x) into a Taylor series using Taylor's Formula.
- Compute the reciprocal of f(x) = 1 + ∑n≥1 nn xn, up to the x3 term.
- Prove that if f(x) = a1x + a2x2 + ... has a0 = 0, then f(x) has no reciprocal in R[[x]]: that is, there is no g(x) ∈ R[[x]] with f(x) g(x) = 1.
- [W] p 24, Ch 1 Ex #1, 3. Hint: You will need to understand Rules 1−5, [W] pp 33−38.
- Prove that if f(x) = ∑n≥0 anxn ∈ R[[x]] satisfies
f '(x) = f(x), then:
f(x) = c exp(x) = c(1 + x + x2⁄2! + x3⁄3! + ⋯) Note: You cannot use the usual theory of differential equations, since that is only valid for convergent power series. You must work coefficient by coefficient. - Catalan numbers Cn.
Step 1. Show that the Catalan recurrence:Cn = ∑i=0 n−1 CiCn−1−i , starting with C0 = 1, imples the generating function equation:f(x) = 1 + x f(x)2. Deduce that:f(x) = 1⁄2x (1−√1−4x ). Step 2. Find the Taylor series of x f(x) = ½ − ½√1−4x , and derive the explicit formula: Cn = 1⁄(n+1) (2n | n).
Hint: Use Taylor's Formula, or the Known Series (1+z)n = ∑k≥0 nk⁄k! zk with n = ½ and z = −4x . - Extra Credit: Recall the Axioms 1− 8 of a ring, and also Axiom 9, multiplicative commutativity: a•b = b•a. Prove all the Axioms 1−9 for R[[x]], showing it is a ring. To prove each equation, you must evaluate the formal series on the left and right sides, according to the definitons of + and •, and check that the coefficients are the same.
- Reciprocals
- To start the first part, find the series cos(x) = ∑n≥0 anxn via Taylor's Formula an =
f(n)(0)⁄n! ,
applied to the derivatives cos'(x) = −sin(x), cos''(x) = −cos(x),
cos'''(x) = sin(x), cos(4)(x) = cos(x). Then:
cos(x) = 1 − x2⁄2! + x4⁄4! − ⋯ . Then apply the formula from the Lemma. For the alternative method based on the geometric series, see [W] p 202 Solution #1. - Starting with a0 = 1 and an = nn, and using the formula from the Lemma, we get:
b0 = 1⁄a0 = 1;
and b1 =
− a1b0⁄a0 = −1, then:
b2 = − 1⁄a0(a1b1 + a2b0) = −(−1 + 22) = −3 , Hence the reciprocal series starts as: g(x) = 1⁄f(x) = 1 − x − 3x2 − 20x3 − ⋯ . We can verify this by typing into Wolfram Alpha:
b3 = − 1⁄a0(a1b2 + a2b1 + a3b0) = −(−3 − 22 + 33) = −20 .
power series 1/(1 + x + 2^2 x^2 + 3^3 x^3) Since the denominator is accurate up to the x3 term, the reciprocal power series will also be accurate up to the x3 term, but no farther.
There is no reason to expect any simple pattern in the bn coefficients, or any simple formula for g(x). However, we know such a g(x) exists, since the bn are defined recursively: a recursive definition is perfectly rigorous, even if it is not very pretty. - Proof: Let f(x) = a1x + a2x2 + ⋯ have a0 = 0. Then for any g(x) = b0 + b1x + b2x2 + ⋯,
we have:
f(x) g(x) = a1b0x + (a1b1+a2b0)x2 + ⋯ . Since this product has constant term 0, it can never equal 1 = 1 + 0x + 0x2 + ⋯, which has constant term 1. Thus, f(x) g(x) ≠ 1 for any possible series g(x).
- To start the first part, find the series cos(x) = ∑n≥0 anxn via Taylor's Formula an =
f(n)(0)⁄n! ,
applied to the derivatives cos'(x) = −sin(x), cos''(x) = −cos(x),
cos'''(x) = sin(x), cos(4)(x) = cos(x). Then:
- See [W] p 197, Solutions #1, 3. You should be able to work out the derivatives explicitly, so
review.
- Given an arbitrary unknown f(x) = ∑n≥0 anxn ∈ R[[x]], its derivative is f '(x)
=
∑n≥1 nanxn−1
=
∑n≥0 (n+1}an+1 xn.
By definition, the equation f '(x) = f(x) means that the coefficients on the two sides are equal:
that is, an = (n+1)an+1. Thus, we have the recurrence:
an+1 =
an⁄(n+1)
for n≥1, starting from some constant a0 = c. This obviously solves to:
an = c 1⁄n!,
and f(x) = ∑n≥0 c xn⁄n! = c exp(x) as desired.
Here we consider exp(x) = ∑n≥0 xn⁄n!
as a known series, or simply a definition of exp(x).
- Catalan numbers.
Step 1. See [HHM] pp 186-187 or [W] p 44.
Step 2. From Math 481 HW 10/4, we recall: h(x) = ½ − ½(1−4x)1/2 , h'(x) = (1−4x)−1/2 , h''(x) = ½(4)(1−4x)−3/2 , h'''(x) = (1⁄2)(3⁄2)(42)(1−4x)−5/2, and:
h(k)(x) = (1⁄2)(3⁄2)...(2k−3⁄2)(4k−1)(1−4x)−(2k−1)/2, so
Hence Ck = ak+1 = 1⁄k+1 (2k | k).ak = h(k)(0) / k! = (1⁄2)(3⁄2)...(2k−3⁄2) 4k−1 / k! = (1)(3)(5)...(2k−3) 4k−1 / 2k−1 k! = (1)(3)(5)...(2k−3) 2k−1(k−1)! / (k−1)! k! = (1)(3)(5)...(2k−3) (2)(4)(6)...(2k−2) / (k−1)! k! = (2k−2)! / (k−1)! k! = 1⁄k (2k−2 | k−1) .
- Reciprocals in R[[x]].
To compute 1⁄f(x) , you can work coefficient by coefficient using the recursive formula in the Lemma above.
Alternatively, if a0 = 1, substitute the series z = −∑n≥1 anxn into the geometric series
1⁄(1−z)
= 1 + z + z2 + ⋯ .
- 1/27: Rules to manipulate sequences and generating functions
Reading:- [W] Ch 2.2, pp 33-39.
- Notes 1/24−1/27.
- Make sure you can use Rules 1−5, and can compute derivatives.
- Re-do HW 1/24 #3,4, explicitly using Wilf's Rules.
Hints:
- For #3, modify Rule 2 to apply to Df(x) = f '(x), rather than x Df(x) = x f '(x).
- For #4, start with the recurrence Cn+1 = C0Cn + C1Cn−1 + ⋯ for n≥0.
- Find the Taylor series of
f(x)
= log(1⁄(1−x))
= −log(1−x),
starting from the fact that Df(x) = 1⁄(1−x).
Hint: Do this by Taylor's Formula, then alternatively using Wilf's Rule #2. - [W] p 65, Ch 2 Ex #4.
Hint: A sequence like {1}4∞ means a0 = ⋯ = a3 = 0, and an = 1 for n≥4. - [W] p 65, Ch 2 Ex #6.
Hint: An example of f(n,k) is:f(4,3) = sum of all products (i1)(i2)(i3), where i1,i2,i3 ≥ 1 with i1 + i2 + i3 = 4 Fix k, and take the generating series fk(x) = ∑n≥0 f(n,k)xn. Apply Rule 4.
= (2)(1)(1) + (1)(2)(1) + (1)(1)(2) = 6.
- HW 1/24 #3. For f(x) = ∑n≥0 anxn,
we have:
Df(x) = f '(x) = ∑n≥0 nanxn−1 = 0a0 + ∑n≥0 (n+1)an+1xn. Hence the modified Rule 2:{(n+1)an+1}n≥0 ↔opsDf(x). (This also follows by combining Rule 2 with Rule 1, seeing as Df(x) = (x Df(x) − 0)⁄x .) Now, if Df(x) = f(x), then (n+1)an+1 = an, which can be immediately solved to give an = c⁄n!, where c = a0, i.e. f(x) = c exp(x).HW 1/24 #4. We did this in class. Assuming {Cn} ↔ops f(x), we apply the ops correspondence to both sides of the recurrence equation: Cn+1 = C0Cn + C1Cn−1 + ⋯ + CnC0 for n≥0. We apply Rule 1 on the left side, Rule 3 or 4 on the right side, and we equate the two generating functions:
(f(x) − C0) ⁄x = f(x)2. Rearranging, we get x f(x)2 − f(x) + 1 = 0, which gives the explicit formula for f(x) in the Solution to HW 1/24 #4. Step 2 is as before. - Assuming f(x) = −log(1−x) = ∑n≥0 anxn, we get the nth derivative as:
Dn f(x) = f (n)(x) = (n−1)!(1−x)−n. Hence, by Taylor's formula, for n≥1:an = f (n)(0)⁄n! = (n−1)!⁄n! = 1⁄n . Also a0 = f(0) = 0. Thus:f(x) = log(1⁄(1−x)) = x + x2⁄2 + x3⁄3 + x4⁄4 + ⋯ . Alternatively, the basic formula f '(x) = 1⁄(1−x) implies x Df(x) = x⁄(1−x). Applying Rule 2 to the left side, and equating the coefficient sequences, we get nan = 1 for n ≥ 1 (also 0a0 = 0). That is, an = 1⁄n , which agrees with the previous calcuation. - See [W] p 203, Ch 2 Solution #4.
- See [W] p 203, Ch 2 Solution #6.
- 1/29: Exponential generating functions
Reading:- [W] Ch 2.3, pp 39−45. Learn Wilf's Rules 1'−3' for ↔egf .
- Review of differential equations.
- More practice with Wilf's Rules 1−5 for
↔ops .
For each sequence, give a formula for the corresponding power series, in terms of x and/or f(x), assuming {an}n≥0
↔ops f(x)
.
- {3n}
- {n2}
- {n2an}
- {n23n}
- { ∑i=0ni23i }
- { ∑i=0ni23n−i }
- { ∑i+j+k=n i2 3j ak }n≥0
- {1⁄n}n≥1
- {1⁄(n+1)}n≥0
- [W] p 24, Ex 2, 4.
- In class, we considered the exponential generating function of the Fibonacci numbers:
F(x) = ∑n≥0 Fn⁄n! xn. We showed this function is a particular solution of the linear, homogeneous, constant-coefficient differential equation:f ''(x) − f '(x) − f(x) = 0. We wish to prove that the only solutions f(x) ∈ R[[x]] are of the form f(x) = A exp(αx) + B exp(βx), where A,B are arbitrary constants, and r = α, β are the roots of the characteristic polynomial equation r2 − r − 1 = 0. Hence F(x) = A exp(αx) + B exp(βx) for appropriate A,B, which implies the explicit formula Fn = Aαn + Bβn.- Prove that f(x) = A exp(αx) + B exp(βx) does indeed satisfy the differential equation.
- Prove that the entire sequence {an}n≥0 is determined by the two initial values a0 and a1 .
- For a solution f(x), with any given initial conditions f(0) = a0 and f '(0) = a1 , find the appropriate function A exp(αx) + B exp(βx) which produces the same initial conditions, and show that f(x) = A exp(αx) + B exp(βx) . This is what we wanted to prove.
- Even more practice with Wilf's Rules 1−5 for
↔ops .
Generalize Rule 3 to the following Mulitplication Rule (given in class): For any list of power series f(x) ↔ops {an}, g(x) ↔ops {bn}, h(x) ↔ops {cn}, etc., their product has coefficients as follows:f(x) g(x) h(x) ⋯ ↔ops { ∑i,j,k,... aibjck⋯ }n≥0, where the sum is over all non-negative integers i,j,k,... which add up to n = i + j + k + ⋯ .
Show how each of the following Wilf Rules is a special case of the Multiplication Rule. That is, explain how to specialize the Multiplication Rule to get the given Wilf Rule.- Rule 3
- Rule 4
- Rule 5
- Rules for ops
- Substituted geometric series: 1⁄(1−3x) .
- Rule 2 applied to geometric series: (xD)2(1⁄(1−x))
=
(x+x2)⁄(1−x)3 .
Wolfram Alpha input: x*(d/dx(x*(d/dx(1/(1-x))))) . - Rule 2 applied to f(x): (xD)2f(x)
= x(x f '(x))' = x f '(x) + x2 f ''(x).
- Rule 2 applied to substituted geometric series from (a):
(xD)2(1⁄(1−3x))
=
(3x+9x2)⁄(1−3x)3 .
- Rule 5 applied to (d):
1⁄(1−x)
• (3x+9x2)⁄(1−3x)3
=
(3x+9x2)⁄(1−x)(1−3x)3
.
- Rule 3 applied to (b) and (a):
(x+x2)⁄(1−x)3 •
1⁄(1−3x) .
- Rule 3, generalized to 3 factors:
(x+x2)⁄(1−x)3 •
1⁄(1−3x)
• f(x)
- HW 1/27 #2: log 1⁄(1−x) .
Note: In mathematical writing, log(x) always means the natural logarithm, with the base-10 logarithm
written as log10(x).
- Rule 1 applied to (h): (log 1⁄(1−x) − log 1⁄(1−0) ) • 1⁄x = 1⁄x log 1⁄(1−x) .
- Substituted geometric series: 1⁄(1−3x) .
- See [W] p 197−198, Ch 1 Solutions #2, 4.
- Fibonacci differential equation.
- Expand the formula f(x) = A exp(αx) + B exp(βx)
into a power series using the definition
exp(x) = 1 + x + x2⁄2! + x3⁄3! + ⋯ .
Differentiate term-by-term, as in the definition in the Notes, and find that:
f ''(x) − f '(x) − f(x) = (α2−α−1) A exp(αx) + (β2−β−1) B exp(βx) = 0, because α, β are solutions of the characteristic equation. - The equation f ''(x) − f '(x) − f(x) = 0 is equivalent to the recurrence an+2 = an+1 + an for n≥0, so that an is clearly determined by the initial values a0, a1.
- Now suppose f(x) = ∑n≥0 anxn is an arbitrary solution of the differential equation, with some initial values a0, a1.
Solving:
A + B = a0 and Aα + Bβ = a1, we get:A = (a1−βa0)⁄(α−β) and B = (αa1−a0)⁄(α−β) . Taking these values of A,B gives g(x) = A exp(αx) + B exp(βx) the same initial coefficients a0 and a1 as f(x). The differential equation guarantees the same coefficient recurrence for f(x) and g(x), so they have all the same coefficients; that is, they are the same power series: f(x) = g(x) as desired.
- Expand the formula f(x) = A exp(αx) + B exp(βx)
into a power series using the definition
exp(x) = 1 + x + x2⁄2! + x3⁄3! + ⋯ .
Differentiate term-by-term, as in the definition in the Notes, and find that:
- The general Multiplication Rule and Wilf's Rules
- Apply the Multiplication Rule to only two series f(x) and g(x), getting the double summation of aibj over all i,j ≥ 0 with i+j = n, and evaluate this as a single summation of aibn−i over i = 0,...,n. This gives Rule 3.
- Apply the Multiplication Rule to k factors, each of which is the same series f(x) ↔ops {an}. This gives Rule 4.
- Apply the Multiplication Rule to the two factors f(x) ↔ops {an} and 1⁄(1−x) ↔ops {1}, and evaluate the double summation of (ai)(1) over all i,j ≥ 0 with i+j = n as the single summation a0 + a1 + ⋯ + an. This gives Rule 5.
- 1/31: Exponential generating functions
Reading:- [W] Ch 2.3, pp 39−45. Learn Rules 1'−3'.
- Again: [W] p 24, Ex 2, 4.
Hints: For [W] Ex 2(a)−(e), apply Rule 2' to {1} ↔egf ex. For [W] Ex 2(f), (g), and some parts of Ex 4, don't use a Rule: just write out the desired power series, and adapt a known exponential power series formula. - Bell numbers and exponential generating functions.
Recall the Bell numbers, which are sums of Stirling partition numbers:
Bn = {n | 1} + {n | 2} + ⋯ + {n | n}. For example, B3 = 5 counts all ways of putting 3 marked balls in any number of exchangeable baskets:123 1|23 2|13 3|12 1|2|3 . Also, we let B0 = 1.- Define a suitable Deletion Transform to prove the recurrence formula:
Bn = ∑ i=0 n−1 (n−1 | i) Bn−1−i for n ≥ 1. Actually, this is rather complicated, so don't spend too much time puzzling over it, unless you want a challenge. Just assume the recurrence, and go on to (b). - Rewrite the recurrence by shifting the left side to Bn+1. Perform the ↔egf correspondence to both sides of the recurrence. (Use Rule 1' for the left side, and Rule 3' for the right side.) Write the resulting equation involving the exponential generating function B~(x) = ∑n≥0 Bn xn⁄n!.
- Solve the above equation to get a simple formula for the exponential generating function B~(x).
- Define a suitable Deletion Transform to prove the recurrence formula:
- Extra Credit: The ring of linear differential operators.
- The formal power series form a ring, but we can consider them as a vector space: V = R[[x]]. Namely, we consider the constants c = c + 0x + 0x2 + ⋯ as the scalars, and arbitrary power series f(x) as the vectors. Of course, V is infinite-dimensional.
- Recall that L : V → V is a linear mapping (or linear transformation or linear operator) means L is a function taking vectors to vectors, satisfying, for all scalars c1, c2 and all vectors v1, v2:
L(c1v1 + c2v2) = c1L(v1) + c2L(v2) . (This is a definition you learned in Math 309.) For a finite-dimensional V, the mapping L could be written as a square matrix, but for the infinite-dimensional V, this is not feasible. - For any two linear mappings L1, L2 : V → V, we can add them to get a new operator
L1 + L2 defined by:
(L1 + L2)(v) = L1(v) + L2(v). (On the left is addition of mappings, on the right is addition of vectors.) - We can also "multiply" them by composition to get a new operator
L1L2 defined by:
(L1L2)(v) = L1(L2(v)) . This addition and multiplication makes the set of all linear mappings L : V → V into a ring. - Consider the derivative operation D : V → V defined by D(f(x)) = f '(x). Also, define the multiplication operation M defined by M(f(x)) = x f(x). You will show below that each of these is a linear mapping from V to V.
- Since D and M are linear mappings, so is any repeated sum or composition of these mappings. For example, L = DMD + 3D − 5, means:
L(f(x)) = D(M(D(f(x)))) + 3 D(f(x)) − 5 f(x)
Wilf's operation xD is another notation for MD.
= (x f '(x))' + 3 f '(x) − 5 f(x)
= f ''(x) + x f '(x) + 3 f '(x) − 5 f(x) . - Let S be the set of all repeated sums and compositions of D and M, as above. This is clearly a subring of the ring of all linear operators: it is called the Weyl algebra.
- Prove that D and M are linear mappings.
- What are the additive and multiplicative identities 0,1 of the ring S? Define them as operators, not merely as symbols.
- Prove that DM = MD + 1. In particular, the ring of operators is not commutatitive (which is not surprising, since the ring of matrix operators is also not commutative).
- Find a basis for S, thought of as a vector space: that is, an infinite list of operators, such that every element of S can be written uniquely as a linear combination of the basis operators, with constant scalar coefficients.
- See [W] p 197−198, Ch 1 Solutions #2, 4.
- Exponential generating function for Bell numbers
- Deletion transform giving recurrence formula
- We want to prove the identity:
Bn = ∑ i=0 n−1 (n−1 | i) Bn−1−i by transforming the set partitions counted by the left side to some composite objects counted by the right side. - An informal way to do this is stated in [W] p 25 Ch 1 Ex 7. (The statement is in the problem, without any futher solution.)
- Write a set partition as S1|⋯⋯|Sk : that is, the Sj's are disjoint exchangeable subsets with S1∪⋯∪Sk = [n].
-
Define the transform of S1|⋯⋯|Sk by deleting the subset Sj which contains n, and recording S' = Sj\{n} as a separate piece of data at the beginning. Letting |S'| = i, the remaining subsets
S1|⋯|Sj−1|Sj+1|⋯|Sk
have n−1−i total elements, but they do not cover [n−1−i] = {1,2,...,n−1−i};
so we tamp them down by applying the unique order-preserving bijection [n] \ Si → [n−1−i]. Tamping down each subset Sm ⊂ [n] to the corresponding S'm ⊂ [n−1−i],
we get the completed transformation:
S1|⋯⋯|Sk ↦ ( S' , S'1|⋯|S'j−1|S'j+1|⋯|S'k )
where n ∈ Sj , S' = Sj\{n} ⊂ [n−1], |Sj| = i and S'1∪⋯∪S'k = [n−1−i] . - The output of the transformation is of type (n−1 | i) Bn−1−i for any i = 1,,..., n−1, meaning this is the obvious formula which counts the possible output objects. If we can prove the transformation is reversible, this will prove the desired recurrence identity.
-
Example: Take the set partition of type B7:
S1|S2|S3 = 16|347|25 .
We remove S2 = {3,4,7} containing n = 7, and we record S' = {3,4}. The remaining set partition is S1|S3 = 16|25, which covers [n] \ S2 = {1,2,5,6}. The tamping map {1,2,5,6} → {1,2,3,4} is 1↦1, 2↦2, 5↦3, 6↦4, and applying it to S1 and S3 gives the final set partition S'1|S'3 = 14|23 . The completed transformation is:S1|S2|S3 = 16|347|25 ↦ (S' , S'1|S'3) = ({3,4} , 14|23)
- Reverse transform: In the general case, we start with any pair (S', S'1|⋯⋯|S'm), with S' ⊂ [n−1] and S'1∪⋯⋯∪S'm = [r]. First, we recover the original n, which must be n = r + |S'| + 1. Next, we define the spreading map, the unique order-preserving bijection [r] → [n−1] \ S'. Applying the spreading map to S'1,..., S'm recovers all the original sets S1,..., Sm, except for the set containing n, which is just Sm+1 = S' ∪ {n}.
-
Reversing the above example, we start with:
(S', S'1|⋯S'2) = ({3,4} , 14|23). We know S' = {3,4} was removed from [n−1] to leave r = 4 elements, so we must have had n = r + |S'| + 1 = 4 + 2 + 1 = 7. The spreading map thus takes:{1,2,3,4} → [n−1] \ S' = {1,2,3,4,5,6} \ {3,4} = {1,2,5,6} ; that is, 1↦1, 2↦2, 3↦5, 4↦6. Applying this to S'1 = {1,4} gives S1 = {1,6}, and similarly S2 = {2,5}. The set which was removed was S3 = S' ∪ {n} = {3,4,7}. Hence the original set partition was:16|25|347 , which is indeed correct, except for the exchange of baskets, which is irrelevant. - Checking that the two transformations reverse each other starting from either side, we have proved the recurrence formula.
- OK, this was a bit much to expect from you, especially the part about tamping and spreading. This is the kind of thing you would encounter in a graduate combinatorics course.
- We want to prove the identity:
- Now write the recurrence formula as:
Bn+1 = ∑i=0 n (n | i) Bn−i for n ≥ 0. Applying Rule 1' (exponential shift of index) to the left side and Rule 3' (exponential convolution formula) the right side, we get:d⁄dx B~(x) = ex B~(x) . -
Writing y = B~(x), we have:
dy⁄dx = ex y.
This is a separable differential equation, and can easily be solved. We transpose to:
1⁄y dy = ex dx,
and integrate:
log(y) = ∫ 1⁄y dy = ∫ ex dx = ex + c
for some constant c. Solving for y gives y = B~(x) = C exp(ex) for some C = ec > 0. The initial condition B~(0) = B0 = 1 forces C = e−1, so that B~(x) = e(ex − 1) = exp(ex − 1).
- Deletion transform giving recurrence formula
- 2/3: Cards, Decks and Hands (1)
Reading:- Notes 2/3
- [W] Ch 3, pp 73−76.
- Prove the following identity discussed in the context of the cooler example, for n = 2m:
(n | 2) (n−2 | 2) ⋯ (2 | 2) = (2m)!⁄(2!)m .
This is the number of ways to partition the set [n] into m two-element subsets [n] = S1 ∪ ⋯ ∪ Sm , where the order of the Si's matters.
Extra Credit: Explain directly why the right-hand expression counts such partitions. - The "original" example of cards, decks, and hands.
Define an exponential family whose pictures are the 4 suits of ordinary playing cards:
P = {♠, ♣, ♥, ♦}, each with weight 1.
A card C = (j,p) consists of a picture (a suit) p ∈ P and a number label (face value) j = 1,2,3,... . (Let us imagine cards for which these numbers go arbitrarily high.)
- What sets of cards make a hand for this exponential family? Hint: Carefully read the definition of a hand. It is not just any set of cards: rather, a special kind of set. What kind?
- How to determine the weight of a hand, according to the definitions?
- Determine the deck-enumerator series d(x) = ∑i≥0 di
xi⁄i! ,
where di is the number of pictures with weight i.
Note that according to our definitions, the deck is not the set of all possible cards: there is only one card for each picture (for each suit). What are those cards? - Apply the exponential formula to determine the hand-enumerator series h(x) = ∑n≥0 hn xn⁄n! , where hn is the number of hands of weight n.
- Adapt the Notes to prove the above formula for h(x).
- Use the formula for h(x) to determine hn explicitly.
- Explain the formula for hn in combinatorial terms
- Extra Credit: In class, we used exponential generating functions to get the recurrence:
(n+1)! = = ∑i=0n (n | i) i! (n−i)! . This is very easy to prove algebraically. However, I would like you to interpret this as a recurrence for the sequence an = n! obtained through a Deletion Transform. That is, given a permutation written as an ordering of [n+1], delete a certain element and produce some data naturally counted by the right-hand side: namely, a subset S ⊂ [n], a permutation of [i], and another permutation of [n−i]. Explain how to recover the original permutation from this data.
Hint: Use an order-preserving tamping and spreading maps.
- (n | 2) (n−2 | 2) ⋯ (2 | 2) = n(n−1)⁄2! (n−2)(n−3)⁄2! ⋯ (2)(1)⁄2! = n!⁄(2!)m = (2m)!⁄(2!)m .
- Exponential family of playing cards.
- The labels in a hand must be the numbers {1,2,...,n} = [n], where n is the weight of the hand.
In this case, each card has weight 1, so a hand is any set of n cards with each label 1,2,...,n appearing exactly once. (You could call this a straight with low-card 1 and high-card n.)
For example, a legal hand is:
{(2,♠), (3,♥), (5,♥), (1♦), (4,♦)} = {(1♦), (2,♠), (3,♥), (4,♦), (5,♥)}.
Two types of sets which are illegal, and do not count as hands in this family:{(1,♦), (2,♠), (2,♥), (4,♦), (5,♥)} or {(1♦), (2,♠), (4,♥), (5,♦), (6,♥)}.
- Each picture has weight 1, and hence so does every card. The weight of a hand is thus simply the number of cards.
- There are 4 pictures with weight 1, and none with any other weight: d1 = 4 and di = 0 for i ≠ 1. Hence d(x)
= 4x.
By definition, the deck of this family is not the set of all possible cards: rather, it has just one standard card for each picture: D = {(1,♠), (1,♣), (1,♥), (1,♦)}, i.e. only the ace as a sample of each suit. - The exponential formula says: h(x) = exp d(x) = e4x.
- We can prove (d) as in the
Notes: In a hand of weight n,
the set [n] must be partitioned into 4 sets (allowing empty sets); and
the number of ways to do this is (as in Ex 1 above):
hn = ∑i1,...,i4 (n | i1) (n−i1 | i2) (n−i1−i2 | i3) (n−i1−i2−i3 | i4)
= ∑i1,...,i4 n!⁄(i1! i2! i3! i4!) ,
where the summation runs over integers i1,...,i4 ≥ 0 with i1 + i2 + i3 + i4 = n. It is easily seen by generalizing [W] Rule 3' (exponential convolution), that this has generating function:h(x) = (∑i≥0 xi⁄i!)4 = e4x .
- Since e4x = ∑n≥0 4n
xn⁄n!,
we have an = 4n.
- Retrospection: Choosing a hand of weight n is equivalent to choosing a suit for each of the labels 1,2,...,n. Each choice is independent with 4 possiblilities, so we use the ordinary Product Principle to get hn = (4)⋯(4) = 4n. This is obvious in hindsight, but we might not notice it if we lay out the cards suit by suit rather than in face value order.
- The labels in a hand must be the numbers {1,2,...,n} = [n], where n is the weight of the hand.
In this case, each card has weight 1, so a hand is any set of n cards with each label 1,2,...,n appearing exactly once. (You could call this a straight with low-card 1 and high-card n.)
For example, a legal hand is:
- 2/5: Examples of Exponential Families
Reading:- Notes 2/5.
- [W] Ch 3.3, pp 76−78.
- Exponential family of graphs.
- Write down all the connected graphs with n = 1,...,4 vertices, which is the most simple-minded way to find c1, ... ,c4. (For c4, group them into types, and just say how many of each type without drawing them all.)
- Compare the above numbers to g1,..., g4. What percentage of all graphs are connected in each case?
Extra Credit: Look for trends in cn⁄gn for larger n (using the online list cn at the OEIS). Can you explain these trends in some way? - Work out the exponential formula c(x) = log g(x) up to the x4 term.
Do this by hand, and check your work on Wolfram Alpha.
Hints: Recall that g0 = 1, so you can write g(x) = 1 + z and use the power series for log(1+z). In your computation, ignore all terms of degree x5 and higher, which will not affect the coefficients c1,...,c4.
- Consider the exponential family of set partitions, having the deck-enumerator d(x) = ex
− 1, and hand-enumerator:
B(x) = ed(x) = 1 + d(x) + 1⁄2! d(x)2 + 1⁄3! d(x)3 + ⋯ ..
- Consider the function f(x) = 1⁄2! d(x)2, which is one of the terms of B(x). Expand this into a Taylor series f(x) = ∑n≥0 an xn⁄n!, and give a simple formula for the coefficient an.
- Using [W] Rule 3', give a more complicated convolution formula for the above coefficients an. Examine this to show that an counts partitions of [n] into exactly 2 non-empty subsets. What is our usual notation for this number?
- Extra Credit: Find the coefficients of 1⁄n! d(x)n. Interpret the coefficient of xn⁄n! as counting a certain special kind of set partitions of [n]. Justify your interpretation.
- Exponential family of graphs
- We have c1 = 1, c2 = 1, c3 = 4, c4 = 38. See the entry in the Online Encyclopedia of Integer Sequences.
- For n = 2, there is c2 = 1 connected graph ①−②, and 1 disconnected graph ① ②.
- For n = 3, there are c3 = 4 connected graphs: the three paths ①−②−③ , ①−③−② , ②−①−③; and also the complete graph with all 3 possible edges. Note that there are only 3!⁄2 = 3 paths, because reflecting a path horizontally (or performing any symmetry on a graph) does not make a different graph.
- For n = 4, there are c4 = 38 connected graphs: 42 = 16 trees by Cayley's Theorem; plus 4!⁄8 = 3 four-cycle graphs (since a four-cycle has 2(4) = 8 symmetries); plus 4!⁄2 = 12 graphs consisting of a three-cycle with an extra edge (which has 2 symmetries); and 4!⁄4 = 6 graphs with five edges (a square with a diagonal, which has 4 symmetries); plus 1 complete graph with all possible edges.
- Proportion of connected graphs to all graphs: cn⁄gn
> n 1 2 3 4 5 cn / gn 1 1⁄2 1⁄2 19⁄32 91⁄128 1 0.5 0.5 0.59 0.71 - Letting z = x
+ 2(2 | 2) x2⁄2!
+ 2(3 | 2) x3⁄3!
+ 2(4 | 2) x4⁄4!
+ ⋯ ,
we get:
c(x) = log(1 + z) = z − z2⁄2 + z3⁄3 − z4⁄4 + ⋯
The Wolfram Alpha input was:
= x + 1⁄2 x2 + 2⁄3 x3 + 19⁄12 x4 + ⋯ .
= 1 x + 1 x2⁄2! + 4 x3⁄3! + 38 x4⁄4! + ⋯ .expand z - z^2 / 2 + z^3 / 3 - z^4 / 4
where z = x + 2 x^2 / 2! + 2^3 x^3 / 3! + 2^6 x^4 / 4! .
- We have c1 = 1, c2 = 1, c3 = 4, c4 = 38. See the entry in the Online Encyclopedia of Integer Sequences.
- Exponential family of set partitions
- f(x) = 1⁄2!
d(x)2 =
1⁄2!(ex − 1)2
=
1⁄2!(e2x − 2ex + 1).
Thus, the coefficient of xn⁄n!
is an = 2n−1 − 1.
- an = 1⁄2! ∑ i=1n−1(n | i)(1)(1). This is the number of partitions of [n] into just two non-empty subsets. We can see such a partition as choosing the first subset of i elements, then putting the rest into the second subset; we also divide by 2! since the sets are exchangeable.
- f(x) = 1⁄2!
d(x)2 =
1⁄2!(ex − 1)2
=
1⁄2!(e2x − 2ex + 1).
Thus, the coefficient of xn⁄n!
is an = 2n−1 − 1.
- 2/7: Quiz 13 Solutions
- 2/7: Proof and analysis of the Exponential Formula
Reading:- Notes 2/7.
- [W] Ch 3.4-3.6, pp 78−83. Wilf's approach to the Labeled Product Principle is somewhat different from my Notes, bypassing the discussion of ordered hands. He uses a two-variable generating function H(x,y), where the coefficient of xnyk⁄n! is h(n,k) = h(k)n , the number of unordered k-card hands of weight n.
- Recall from Notes 2/5 that the Bell numbers Bn count partitions of [n] into any number of subsets, which is equivalent to hands of weight n in the exponential family of set partitions, whose pictures are sets of unlabeled balls. Their generating function is B(x) = exp(ex − 1).
We can refine this to consider only partitions of [n] into k non-empty subsets, which are counted by the Stirling partition numbers {n | k}, so that Bn = {n | 1} + {n | 2} + ⋯ + {n | n}. In terms of the exponential family, k-subset partitions of [n] correspond to k-card hands of weight n, as in Notes 2/7 #3, so that {n | k} = h(k)n .
Problems:- Use the analysis in the Notes to find a simple formula for the exponential generating function of the Stirling partition numbers {n | k} for fixed k:
fk(x) = ∑n≥0 {n | k} xn⁄n! = {1 | k} x⁄1! + {2 | k} x2⁄2! + {3 | k} x3⁄3! + ⋯ . - Use your formula for the generating function to find a formula for {n | k}. Where have you seen this before?
- Expand the formula B(x) = exp(ex − 1) into a Taylor series by algebraic methods, to obtain a completely new and surprising formula for Bn, different from Bn = {n | 1} + {n | 2} + ⋯ + {n | n}.
- Use the analysis in the Notes to find a simple formula for the exponential generating function of the Stirling partition numbers {n | k} for fixed k:
- We saw after Quiz 13 (2/7) that a hand in the exponential family of directed cycles corresponds to the cycle decomposition of a permutation (see also Wilf p. 77).
Applying today's Notes to this family,
find the exponential generating function of the Stirling cycle numbers [n | k],
which count the permutations of [n] having k cycles.
We have seen these before in Notes 1/13, HW 1/13 #1, and see also [HHM] p. 227−230. - Extra Credit: Let an be the number of permutations of [n] having only cycles of odd length (no 2-cycles, 4-cycles, etc.). For example, a4 = 9 counts the permutations (in cycle notation):
(1)(2)(3)(4), (1)(234), (1)(243), (2)(134), (2)(143), (3)(124), (3)(142), (4)(123), (4)(132). Use the Notes to find the exponential generating function of {an}.
Hint: To extract only the odd terms of the Taylor series of a function f(x), take ½ (f(x) − f(−x)).
- Formulas for set partitions
- We know k-subset partitions of [n] correspond to unordered k-card hands of weight n in the
exponential family of set partitions, which has deck-enumerator d(x) = ex − 1.
Notes 2/7 #3 deals with such hands: Proposition 3 says the generating function is the kth term of h(x) = exp d(x), namely:
fk(x) = ∑n≥0 {n | k} xn⁄n! = h(k)(x) = 1⁄k! d(x)k = 1⁄k! (ex − 1)k - Expanding this by the Binomial Theorem gives:
fk(x) = 1⁄k! ∑j=0k (k | j) ejx (−1)k−j. Taking the the Taylor series of ejx gives (a flipped form of) the familiar formula from the Twelvefold Way:{n | k} = 1⁄k! ∑j=0k (−1)k−j (k | j) jn.
- Given the generating function formula B(x) = exp(ex − 1),
the basic method of Step 2 is to get B(x) as a sum of functions with known power series: in this case, in terms of erx. First, we can get rid of the −1 in the exponent:
B(x) = 1⁄e exp ex. Next, we expand the exp(z) into a power series, with z = ex and zj = ejx:
B(x) = 1⁄e ∑j≥0 ejx⁄j! = 1⁄e ∑j≥0 ∑n≥0 (jx)n⁄j!n! .
Bn = 1⁄e ∑j≥1 jn⁄j! .
B3 = 1⁄e (1 + 23⁄2! + 33⁄3! + 43⁄4! + 53⁄5! + ⋯) =
I don't think we would have thought of this by combinatorial reasoning, do you?
Extra Credit: For general n, how many terms of this series do we need, so that rounding to the nearest integer gives Bn? Are n terms enough, or n/2, or √n? If we knew this, it would give a finite formula for Bn, perhaps even an efficient formula.
For more on Bell numbers, see Wikipedia.
- We know k-subset partitions of [n] correspond to unordered k-card hands of weight n in the
exponential family of set partitions, which has deck-enumerator d(x) = ex − 1.
Notes 2/7 #3 deals with such hands: Proposition 3 says the generating function is the kth term of h(x) = exp d(x), namely:
- A permutation of [n] with exactly k cycles corresponds to
an unordered k-card hand of weight n in the family of directed cycles,
which has deck-enumerator
d(x) =
log(1⁄1−x) .
Thus, the Stirling cycle numbers are [n | k] = h(k)n ,
and again using Notes 2/7 Proposition 3, the generating function for fixed k is:
h(k)(x) = ∑n≥0 {n | k} xn⁄n! = 1⁄k! d(x)k = 1⁄k! logk(1⁄1−x) .
See also Wilf Ch 3.5, p. 81
- 2/10: Exponential Families Wrap-up
Reading:- Notes 2/7 from last time.
- Recall that the ordered Bell numbers Rn count lists of sets.
That is, Rn is the number of ways to partition the set [n] into any number of subsets (S1,..., Sk), where the order of the subsets matters.
For example, R3 = 13 counts the partitions:
123 1|23 23|1 2|13 13|2 3|12 12|3 (Compare this to the unordered Bell numbers Bn from last time, which enumerate unordered hands of the family of set partitions.)
1|2|3 1|3|2 2|1|3 2|3|1 3|1|2 3|2|1- How many possible outcomes of a race with n horses, allowing ties? For example, for n = 6 horses, we could have 3,6 tied for first place, 4 in second place, and 1,2,5 tied for third place. For general n, give your answer in terms of Rn.
- Consider the surjection numbers surj(n,k) from the Twelvefold Way: the number of surjective functions f : [n] → [k]. (We have reversed the previous roles of n and k.) Explain why we have:
Rn = surj(n,1) + surj(n,2) + ⋯ + surj(n,n). Hint: A surjection can be transformed into a list of k subsets of [n]. - If we consider lists of sets as a family, what is the deck? That is, what are the basic objects which are labeled and combined into a list? Find the deck enumerator function d(x).
- Find the enumerator function for the surjection numbers surj(n,k) with k fixed. These are the k-card ordered hands of the family: surj(n,k) = ℓ(k)n. So find a simple formula for:
∑n≥0 surj(n,k) xn⁄n! . = ∑n≥0 ℓ(k)n xn⁄n! = ℓ(k)(x) . Hint: Use Notes 2/7 #2. - Find the enumerator function R(x) = ∑n≥0 Rn xn⁄n! . Hint: Sum the enumerator functions ℓ(k)(x) for k ≥ 0.
- Starting with the formula in (e), expand R(x) into a Taylor series, and get an infinite sum formula for Rn similar to Dobinski's Formula for Bn in HW 2/7 #1(c). Hint: Expand into a double summation over k ≥ 0 and n ≥ 0. Put ∑n≥0 on the outside, and factor out xn⁄n! .
- Sets and lists of singles and pairs. Use exponential families to solve Problems (a)−(d) below.
- Find the appropriate version of decks and hands for the problem.
- Find a simple formula for the exponential generating function using Notes 2/7.
- Expand the generating function into a Taylor series, by algebraic methods if possible, otherwise by brute force (Wolfram Alpha, or try this site).
- Among 10 people working on a project, some work alone, some join up into pairs, in any combination. Example: singles are 2,5,7,10; pairs are 1&9, 3&4, 6&8. How many possible combinations?
- Same as (a), but now the teams are given rankings for their projects. Example: 1st place team is 3&4; 2nd is 7; 3rd is 10; 4th is 1&9; 5th is 6&8; 6th is 2; 7th is 5. How many possible rankings (including all possible team combinations)?
- Same as (a), but in each pair, one person is designated the leader. For example, team 1&9 has leader 1; team 9&1 has leader 9.
- Teams have leaders as in (c), and are ranked as in (b).
- Ordered Bell numbers
- Ways to partition the set of n horses into a first subset, a second subset, etc: this just restates the definition of Rn.
- We can write each function f : [n] → [k] in list notation (f(1),..., f(n)); or in balls-and-bins notation, meaning we record (S1,..., Sk), where Si = {j ∈ [n] with f(j) = i}. (See HW 1/10 #1.) Thus, a surjection f : [n] → [k] is equivalent to
a partition of [n] by a list of k subsets: (S1,..., Sk). Thus Rn , the number of partitions of [n] into a list of any number of subsets, equals the sum of the surjection numbers for all k, as desired.
- The deck is the same as for the family of set partitions: D = { •, ••, •••, .... }, so dn = 1 for n ≥ 1, and d(x) = ex − 1.
- ℓ(k)(x)
= d(x)k
= (ex − 1)k
- Partitons of [n] by lists of k subsets are split into the cases with k = 0,1,2,.... Thus:
R(x) = ℓ(x) = ∑k≥0 ℓ(k)(x) = ∑k≥0 d(x)k
= 1⁄(1 − d(x)) = 1⁄(1 − (ex−1)) = 1⁄(2 − ex) . - We expand the above generating function:
R(x) = 1⁄2 1⁄(1 − ½ex) = 1⁄2 ∑k≥0 (½ex)k
= 1⁄2 ∑k≥0 (1⁄2k) ekx = 1⁄2 ∑k≥0 (1⁄2k) ∑n≥0 knxn⁄n! = ∑n≥0 (∑k≥0 kn⁄2k+1) xn⁄n!
- Ways to partition the set of n horses into a first subset, a second subset, etc: this just restates the definition of Rn.
- Sets and lists of singles and pairs.
-
Step 0: First, we generalize the problem to
an = number of single/pair team combinations from n people,
so that the original problem is a10. This is a set-of-sets model.
Step 1: We want to find the exponential generating function f(x) = ∑n≥0 an xn⁄n! . We start with the deck D = {•, ••}, so d(x) = x + x2⁄2! . A combination of teams corresponds to an unordered hand with any number of cards from D, so by Notes 2/7 #4, the team enumerator is:
f(x) = h(x) = exp d(x) = exp(x + x2⁄2!).
Step 2: We could try expanding this using the Taylor series of exp(z), and the binomial theorem for zk = (x + x2⁄2!)k, but this does not seem worth it. Wolfram Alpha gives the x10 term of the Taylor series as: (1187⁄453600) x10, so:
a10 = 10! (1187⁄453600) = 9496. -
Step 0: This time we let an = number of single/pair team lists from n people.
This is a list-of-sets model.
Step 1: To find the exponential generating function f(x) = ∑n≥0 an xn⁄n! , we start with the same deck D = {•, ••} with d(x) = x + x2⁄2! . A list of teams corresponds to an ordered hand with any number of cards from D, so by Notes 2/7 #2, summed over all k into a geometric series, the team list enumerator is:
f(x) = ℓ(x) = ∑k≥0 d(x)k = 1⁄(1 − d(x)) = 1⁄(1 − x − ½x2) .
Step 2: Again, putting the above function into Wolfram Alpha immediately gives:
a10 = 10! (571⁄32) = 64751400. This is much bigger than in part (a), because it distinguishes all permutations of a given set of teams.We could also expand algebraically using a partial fraction expansion of f(x). Letting x = α = −1−√3 and x = β = −1+√3 be the vertical asymptotes, so that 1 − x − ½x2 = (1 − x⁄α)(1 − x⁄β), we expand as:
f(x) = 1⁄(1 − x − ½x2) = A⁄(1 − x⁄α) + B⁄(1 − x⁄β)
1⁄α = 1−√3⁄2 1⁄β = 1+√3⁄2 A = 3−√3⁄6 B = 3+√3⁄6
an⁄n! = A⁄αn + B⁄βn ≈ B⁄βn = (3+√3⁄6) (1+√3⁄2)n .
-
Step 0: This time
an = number of single/pair team combinations from n people, with a leader in each pair.
Thus, each pair is ordered, and this is a set-of-lists model.
Step 1: We want to find the exponential generating function f(x) = ∑n≥0 an xn⁄n! . This time the deck must take the order of each pair into account:
D = {① , ①→② , ②→①} or {(①) , (①,②) , (②,①)},
f(x) = h(x) = exp d(x) = exp(x + x2).
Step 2: a10 = 10! (19093⁄518400) = 133651.
-
Step 0: Finally,
an = number of single/pair team lists from n people, with a leader in each pair.
This is a list-of-lists model.
Step 1: The deck is the same as in part (c), so and d(x) = x + x2. A list of teams-with-leader corresponds to an ordered hand with any number of cards from D, so as in part (b), the team enumerator is:
f(x) = ℓ(x) = 1⁄(1 − x − x2)
Step 2: Since the exponential generating function of our sequence {an} is the same as the ordinary generating function of the Fibonacci numbers {Fn+1}, we get: an⁄n! = Fn+1, i.e. an = n! Fn+1.
Extra Credit: Explain this formula combinatorially. It seems to be saying that one of our team lists can be transformed into a permutation along with a combinatorial model for the Fibonacci numbers. (We gave some models for the Fibonacci numbers in class, or check Wikipedia.)
-
Step 0: First, we generalize the problem to
an = number of single/pair team combinations from n people,
so that the original problem is a10. This is a set-of-sets model.
- 2/12: Recurrences and asymptotics from generating functions
Reading:- [W] Ch 1.6 pp 22−23: The x Dlog operation
- [W] Ch 5.2 pp 171−177: Asymptotics of poles
-
Derangements. Recall the derangement number Dn, which counts permutations of [n] without fixed points: that is, bijections σ : [n] → [n] with σ(i) ≠ i for every i. For example, D3 = 2 counts the permutations σ = (123), (132) (written in cycle notation); all other permutations (1)(2)(3), (12)(3), (13)(2), (1)(23) have a fixed point, which corresponds to a 1-cycle. In fact, the derangements are precisely the permutations with no 1-cycles. In class on 2/7, we used this to find the exponential generating function D(x) = ∑n≥0 Dn
xn⁄n! .
(Do not confuse this with a deck-enumerator function d(x).)
- From Quiz 13 on 2/7, recall the exponential family of directed cycles with deck-enumerator dn = (n−1)! and d(x) = log 1⁄(1−x) . The unordered hands of this family model the cycle notation for permutations. Remove the 1-cycles from the family to model the derangements, and use the exponential formula to find the derangement generating function D(x).
- Given D(x) = e−x⁄(1−x) , clear denominators to find a recurrence for Dn. (The result is rather mysterious: Extra Credit for a combinatorial explanation.)
- Find the poles (vertical asymptotes) of D(x) for x in the complex plane. Find the principal part A⁄(1−x/α), and give an asymptotic formula Dn⁄n! ≈ A ⁄αn.
- Finally, apply Stirling's approximation for n! to give an asymptotic for Dn. How many digits should there be in D100?
- Recurrences from x D log. Given a generating function {an} ↔egf f(x)
where f(x) has no denominator, we need a different approach to finding a recurrence for an. We use the "x Dlog method" ([W]
p 22).
It says that if
f(x) = exp d(x), then you perform the composite operation x D log f(x) on the left side, and the corresponding operation on the right side. (That is, on each side you take log, then the derivative D = d⁄dx, then multiply by x.) The result is the formula:x f '(x)⁄f(x) = x d'(x) .
- Explain why the left side is: x D log f(x) = x f '(x)⁄f(x) . Explain why the right side is x D log ed(x) = x d'(x).
- Clear denominators in the above formula, and convert it into an equation involving Taylor coefficients, using Wilf's ↔egf rules (p. 40−42).
- Apply the x Dlog operation to give a recurrence for the coefficients of ex+x2, which appeared in HW 2/10 #2(c).
- Apply the x Dlog operation to give a recurrence for the Bell numbers, which have generating function B(x) = exp(ex − 1).
- Try the x Dlog operation on the generating function from #1 above, D(x) = e−x⁄(1−x). (Here the right-hand side is not exp of something, but you can still compute x Dlog of it by calculus.) Does this give a better or worse recurrence than clearing denominators?
- Asymptotics of ordered Bell numbers. Recall the numbers
Rn from HW 2/10 #1, with exponential generating function
R(x) = 1⁄(2 − ex) .
We wish to find a simple asymptotic formula for the coefficients Rn .
- To find all vertical asymptotes of R(x) in the complex plane, find all the roots of the denominator (including complex ones). Use the fact that exp(x+iy) = ex(cos y + i sin y), so that exp(x+iy) is a posiitve real number only for y = 2πk for k an integer.
- Find the dominant principal part f(x) = A⁄(1 − x/α) + ⋯ , which contributes most to the coefficients. Here x = α is the vertical asymptote closest to the origin (usually on the positive real line). Find the numerator using A = limx→α R(x) (1 − x/α).
- Since the prinicpal part has a pole (vertical asymptote) closer to the origin than the remainder terms (whatever they may be), the coefficients of R(x) are asymptotic to the coefficients of A⁄(1 − x/α) . Find the asymptotic formula for Rn
- Derangement numbers
- Define an exponential family whose pictures are directed cycles of length at least 2 (no 1-cycles). Thus, the deck-enumerator is:
d(x) = ∑n≥2 (n−1)! xn⁄n! = log 1⁄(1−x) − x .
D(x) = exp d(x) = exp(log 1⁄(1−x)) exp(−x) = e−x⁄(1−x) .
- The left side of the equation (1−x) D(x) = e−x expands into Taylor series as:
(1 − x) ∑n≥0 Dn xn⁄n! = ∑n≥0 Dn xn⁄n! − ∑n≥0 Dn xn+1⁄n!
= ∑n≥0 Dn xn⁄n! − ∑n≥0 (n+1)Dn xn+1⁄(n+1)!
= ∑n≥0 Dn xn⁄n! − ∑n≥1 n Dn−1 xn⁄n!
- Since e−x has no poles (vertical asymptotes) for x in the complex plane (it is an entire function), our D(x) has x = 1 as its only pole. The coefficient of its principal part is:
A = limx→1 (e−x⁄(1−x)) (1−x) = e−1.
Dn = n!(1 − 1⁄1! + 1⁄2! ⋯ ± 1⁄n!).
- Applying Stirling's approximation n! ≈ √2πn
(n⁄e)n, we get:
Dn ≈ e−1√2πn (n⁄e)n.
log10(e−1√2π(100) (100⁄e)100) = −log10(e) + ½ log10(2π) + 1 + 100(2 − log10(e)) ≈ 157.5
- Define an exponential family whose pictures are directed cycles of length at least 2 (no 1-cycles). Thus, the deck-enumerator is:
- The x Dlog method for recurrences
- We apply the composite operation x D log to both sides of the Exponential Formula f(x) = exp d(x).
On the left side, we use log'(z) = 1⁄z and the Chain Rule to get
d⁄dx log f(x) = 1⁄f(x) f '(x),
- We take coefficients on both sides of x f '(x) = x d'(x) f(x).
According to Wilf's Rule 2', the left side is x Df(x) ↔egf n an.
On the right side, x d'(x) ↔egf n dn ,
and the product (x d'(x)) f(x) is an exponential convolution by Rule 3'.
Equating the two sides:
n an = ∑ i=0n (n | i) i di an−i .
an = 1⁄n ((n | 1)d1an−1 + 2(n | 2)d2an−2 + 3(n | 3)d3an−3 + ⋯ + n(n | n)dna0) .
an = d1an−1 + (n−1 | 1)d2an−2 + (n−1 | 2)d3an−3 + ⋯ + (n−1 | n−1)dna0 .
- Letting f(x) = ex+x2 = ed(x) with d(x) = x + 2 (x2⁄2!),
the functional equation
x f '(x) = x (x + 2 x2⁄2)' f(x)
n an = (n | 1)d1an−1 + 2(n | 2)d2an−2 ,
an = an−1 + 2(n−1) an−2 .
- For the Bell number enumerator B(x) = exp(ex − 1) = ed(x) with dn = 1 for n ≥ 1, d0 = 0, carrying through the method gives:
Bn = Bn−1 + (n−1 | 1)Bn−2 + (n−1 | 2)Bn−3 + ⋯ + (n−1 | n−1)B0 .
- The derangement enumerator D(x) =
e−x⁄(1−x)
does not fit the above pattern, so we need to it work out by specially, performing the x D log operation to both sides:
log D(x) = − x + log 1⁄(1−x) ,
x D'(x)⁄D(x) = − x + x⁄(1−x) = x2⁄(1−x) ,
x D'(x) = x2⁄(1−x) D(x) .
n Dn = ∑ i=2n (n | i) i! Dn−i
Dn = (n−1) Dn−2 + (n−1)2 Dn−3 + (n−1)3 Dn−4 + ⋯ + (n−1)n−2 D1 + (n−1)! D0 .
44 = (5−1) 2 + (5−1)(5−2) 1 + (5−1)(5−2)(5−3) 0 + (5−1)! 1 .
- We apply the composite operation x D log to both sides of the Exponential Formula f(x) = exp d(x).
On the left side, we use log'(z) = 1⁄z and the Chain Rule to get
- Asymptotics of Rn
- We have exp(x+iy) = ex(cos y + i sin y) = 2 exactly when the radius is
ex = 2 and the circular part is cos y + i sin y = 1: that is, x = log(2) and y = 0, ±2π,
±4π,....
Clearly, the smallest of these roots log(2) + iy is when y = 0, that is, α = log(2).
- Given α = log(2), we use L'Hôpital's Rule to find:
A = limx→α R(x) (1 − x/α) = limx→α (1 − x/α)⁄(2 − ex)
= limx→α (− 1/α)⁄(− ex) = 1⁄αeα = 1⁄2log(2) .
- Since:
∑n≥0 Rn⁄n! xn = R(x) ≈ A⁄(1 − x/α) = ∑n≥0 A⁄αn xn ,
- We have exp(x+iy) = ex(cos y + i sin y) = 2 exactly when the radius is
ex = 2 and the circular part is cos y + i sin y = 1: that is, x = log(2) and y = 0, ±2π,
±4π,....
Clearly, the smallest of these roots log(2) + iy is when y = 0, that is, α = log(2).
- 2/14: Asymptotics and complex analysis
Reading:- [W] Ch 5.2 pp 171−177: Asymptotics of pole singularities (from last time)
- (optional) [W] Ch 2.4 pp 46−49: Taylor series of a complex variable
- (optional) [W] Ch 5.3 pp 181−183: Stirling's Approximation
- (optional) Notes on Stilrling's Approximation from my graduate course.
- Recall the Catalan numbers Cn from the Twelvefold Way handout and HW 1/24 #4.
- Use the exact formula for Cn and Stirling's Approximation to get an asymptotic formula for Cn .
- How many digits in C100?
- Check the accuracy of your formula against the exact formula for n = 5, 10, 20. What is the percentage error?
- Valentine's Day game.
- A group of n people (numbered 1,..., n) play a game. Each person picks a name at random from a basket, and gives that person a gift. If a person picks his own name, he can choose to buy a gift for himself, or no gift.
- Example: n = 9 people: 1 gives to 5 gives to 2 gives to 9 gives to 1; 3 gives to 7 gives to 4 gives to 3; 8 buys himself a gift; and 6 chooses no gift (after shedding a tear).
- Let an be the number of possible gift-arrangements of the Valentine game with n people.
- Should you use an ordinary or exponential generating function for this problem? How can you tell?
- Step 1: Find a simple formula for the generating function using the appropriate version of the Product Principle.
Hint: A gift-arrangement defines a permutation of [n], since each person is mapped injectively to another person. Consider these permutations in cycle-notation, and take account of the extra choice for each 1-cycle. The Exponential Formula and its variants are the labeled version of the Product Principle. - Step 2: Find an explicit formula for an , if this is reasonably possible.
- Step 2: Find a recurrence (as simple as possible) for computing an.
- Step 2: Find an asymptotic formula for an.
- Which is the most satisfactory result of Step 2? Which has the most right to be called "the answer" to the problem?
- Same as #2, except that if two people choose each other, they can choose to exchange gifts, or to keep the gifts themselves.
Example: n = 9 people: 1 gives to 5 gives to 2 gives to 1; 3 gives to 7 gives to 4 gives to 3; 8 and 9 choose not to exchange gifts; and 6 chooses no gift.
- Catalan number approximation
- Cn
= 1⁄(n+1) (2n | n)
= 1⁄(n+1) (2n)!⁄(n!)2
∼ 1⁄n√2π2n (2n/e)2n⁄(√2πn)2 (n/e)2n
=
4n⁄n3/2√π .
Here we used the asymptotic approximation: 1⁄(n+1) ∼ 1⁄n and Stirling's Approximation n! ∼ √2πn (n/e)n. - The number of base-10 digits for n = 100 is:
log10(4100⁄1003/2√π) = 100 log10(4) − 3⁄2 log10 100 − 1⁄2 log10 π ≈ 56.96 . Thus, C100 is a high 56-digit number, in fact C100 ≈ 1056.96 = 9.06618 × 1056. - Wolfram Alpha input: Catalannumber(n) for n = 5,10,20 or binomial(2n,n)/(n+1) for n = 5,10,20 .
Output:
n 5 10 20 Cn 42 16796 6564120420 4n⁄n3/2√π 52 18708 6.93 × 109 ratio 1.23 1.11 1.06
Clearly, the percentage error is shrinking toward zero, though the absolute error keeps growing.
- Cn
= 1⁄(n+1) (2n | n)
= 1⁄(n+1) (2n)!⁄(n!)2
∼ 1⁄n√2π2n (2n/e)2n⁄(√2πn)2 (n/e)2n
=
4n⁄n3/2√π .
- Valentine game with choice for 1-cycles
- Since the objects being counted (the gift-arrangements) depend on some arrangement of the labels {1,...,n}, it is the exponential generating function (comparing each an to the permutations n!)
which has a better chance to turn out tractable.
Thus, we take f(x) = ∑n≥0 an
xn⁄n! .
- Step 1. Considering the gift-arrangements in cycle-notation as in the example,
they are made up of directed cycles with the labels {1,...,n} distributed among them,
as in Quiz 13.
The only difference is that there are 2 types of 1-cycles: self-gift and no-gift.
Thus, for n ≥ 2, the deck D consists of dn = (n−1)! directed-cycle cards.
For n = 1, we have d1 = 2 cards, each with 1 happy or 1 sad person.
(As always, d0 = 0.)
The deck enumerator is thus:
d(x) = 2x + ∑n≥2 (n−1)! xn⁄n! = x + log 1⁄(1−x) .
f(x) = h(x) = ed(x) = exp(x + log 1⁄(1−x)) = ex⁄(1−x) .
- Step 2: Explicit formula: Wilf's Rule 5 (p
37) applies to formulas like our f(x); but it is a rule for ordinary generating functions,
giving the coefficient of xn, which in our case is an⁄n! :
Thus, it will find:
an⁄n! = 1 + 1⁄1! + 1⁄2! + ⋯ + 1⁄n! ,
- Step 2: Recurrence. Clearing denominators, we get almost the same computation as for derangements (1b), giving:
an = n an−1 + 1 for n ≥ 1.
- Step 2: Asymptotic formula. Again as for derangements (1c), we get an ∼ n! e, which is already clear from the exact explicit formula.
- You use the different answers for different purposes. The recursive formula computes an efficiently, minimizing the number of operations (which you want for hand and for machine computations). You need the exact explict formula to analyze the detailed properties of an, such as whether it is odd or even. The asymptotic approximation formula gives an estimate of its magnitude.
- Since the objects being counted (the gift-arrangements) depend on some arrangement of the labels {1,...,n}, it is the exponential generating function (comparing each an to the permutations n!)
which has a better chance to turn out tractable.
Thus, we take f(x) = ∑n≥0 an
xn⁄n! .
- Valentine game with choice for 1- and 2-cycles
- In principle, this is just like #2, but the details are more intricate, and give you a good technical workout.
- Now there are two types of 1-cycles and of 2-cycles, so:
d(x) = x
+ x2⁄2
+ log 1⁄(1−x) ,
and f(x) =
exp(x + x2/2)⁄(1−x) .
- Step 2: Exact formula. The formula f(x) = exex2/2⁄(1−x) could be expanded with Wilf's Rules, but the result seems too complcated to be of any use: it would be at least a double summation.
- To get a reasonable recurrence, we want an equation like: u(x) f(x) = v(x) with u(x) and v(x) having simple Taylor series. To make up u(x) and v(x), we have three factors to juggle with: ex, ex2/2, (1−x). The best equation seems to be:
(1−x) e−x f(x) = ex2/2. Then:(1−x) e−x = ∑n≥0 (−1)n xn⁄n! − ∑n≥0 (−1)n xn+1⁄n!
= ∑n≥0 (−1)n xn⁄n! + ∑n≥1 (−1)n xn⁄(n−1)! = ∑n≥0 (−1)n(n+1) xn⁄n!Also, ex2/2 = ∑m≥0 (2m)!⁄2m m! x2m⁄(2m)! = ∑n≥0 n!odd xn⁄n! , where we invent the notation: n!odd = (1)(3)(5)⋯(n) for n odd, and n!odd = 0 for n even. (This appeared in HW 1/24 #4.) Applying Wilf's Rule 3' (p 42):
∑ i=0n (n | i) (−1)i (i+1) an−i = n!odd In other words:an = n!odd + ∑ i=1n (n | i) (−1)i+1 (i+1) an−i . - The asymptotic formula is just as easy as before, since the only pole (vertical asymptote) is again x = 1. The residue (coeffiicient in the partial fraction decomposition) is: A = limx→1 (1−x) exp(x + x2/2)⁄(1−x) = e3/2. Then we know f(x) = A⁄(1−x) + ε(x), where ε(x) is a correction term with no poles, which means its Taylor coefficients are much smaller than those coming from the geometric series. That is: an⁄n! ∼ e3/2, and an ∼ n! e3/2.
- In principle, this is just like #2, but the details are more intricate, and give you a good technical workout.
- 2/17: Midterm Review 1
Reading: See Midterm announcement 2/21.
HW:- Jane's Chocolate Shop sells small boxes for $1, large boxes for $2, and deluxe boxes for $3. Do a full analysis of the following counting problems, computing the generating function (ordinary or exponential), an explicit formula (if possible), a recurrence, and an asymptotic formula.
- How many ways to sell $100 worth of chocolates in one day?
Example: 18 small, 29 large, 8 deluxe, for a total sale of 18 + 29(2) + 8(3) = 100. - The cash register printout records each transaction in order. How many ways can this come out, selling $100 worth of chocolates?
Example: small, large, large, small, deluxe,..., giving a total of $100.
- How many ways to sell $100 worth of chocolates in one day?
- Generalizing Prob 1(b), define an = ways to sell $n worth of $1, $2, and $3 boxes, where the order of transactions matters. Construct a Deletion Transform to discover and prove a recurrence for an. (Is this the recurrence you got from generating functions in the previous problem?)
- Continuing Prob 1(b), it turns out Jane puts more than chocolate into her brownies. In fact, all the customers that day are Drug Enforcement Agents, buying with dollar bills invisibly marked #1,..., #100. At the end of the day, they raid the store and confiscate the stack of 100 one-dollar bills.
- How many ways could the 100 bills have been put into the cash register?
Example: First transaction: bills #52, #37. Second transaction: bills #96, #22, #30. Third transaction: bill #16. And so on, until all 100 bills are spent. - Compare the answer with Prob 1(b), and combinatorially explain the relationship between them.
- How many ways could the 100 bills have been put into the cash register?
- Same as Prob 3, but with the order of transactions irrelevant, and the order of bills within each transaction irrelevant.
Example: 18 × $1 boxes, bought with bills #2, #15, #17,.... Also 29 × $2 boxes bought with bills {#7, #49} and {#77, #98} and .... Also 8 × $3 boxes bought with bills {#19, #22, #80} and ....- How many ways could the 100 bills have been spent?
- Compare the answer with Prob 1(a), and explain why you do not have the same kind of relationship that you saw in 3(b).
- Chocolate sales
- Selling $100 worth of $1, $2, $3 boxes, with order irrelevant.
- Step 0: Generalize to a sequence: an = number of ways to sell $n (i.e. n dollars worth).
-
Step 1: Find the generating function. Since the outcomes (chocolate sales of $n) are not objects labeled 1,..., n, we should use ordinary generating functions, summarized in Notes 1/15. There is a simple choice algorithm for producing outcomes of any size:
Translating from logic to algebra and simplifying the geometric series:(choose any boxes of $1, $2, $3) ⇔ (0×$1 or 1×$1 or 2×$1 or ⋯)
and (0×$2 or 1×$2 or 2×$2 or ⋯)
and (0×$3 or 1×$3 or 2×$3 or ⋯) .f(x) = ∑n≥0 anxn = (x0 + x1 + x2 + ⋯) (x0 + x2 + x4 + ⋯) (x0 + x3 + x6 + ⋯)
= 1⁄(1−x) 1⁄(1−x2) 1⁄(1−x3) = 1⁄(1−x)(1−x2)(1−x3) . -
Step 2: Brute force. If we only want the Taylor coefficient a100, Wolfram Alpha gives it as:
a100 = 844.
-
Step 2: Asymptotic formula. This is the easiest way to work out an approximate answer for general n. The poles of f(x) are the complex roots of the denominator: α = 1, β = −1, γ = cos(2π⁄3) + i sin(2π⁄3), δ = cos(2π⁄3) − i sin(2π⁄3).
Now, all of these have |x| = 1, so they might all contribute to the dominant term. However, the root α = 1 has a triple zero in the denominator, and the partial fraction decomposition would be of the form:
f(x) = 1⁄(1−x) 1⁄(1−x2) 1⁄(1−x3)
= 1⁄(1−x) (1−x)(1+x) (1−x)(1 − x/γ)(1 − x/δ)
= 1⁄(1−x)3 (1+x) (1 − x/γ)(1 − x/δ)
= A⁄(1−x)3 + B⁄(1−x)2 + C⁄(1−x) + D⁄(1+x) + E⁄(1 − x/γ) + F⁄(1 − x/δ) .f(x) ≈ A⁄(1−x)3 = ∑n≥0 A ((3 | n)) xn ,
A = limx→1 f(x) (1−x)3 = limx→1 (1−x)3⁄(1−x)(1−x2)(1−x3) = −6⁄−36 . = 1⁄6 .
an ∼ 1⁄6 ((3 | n)) = 1⁄12 (n+1)(n+2) ∼ n2⁄12
-
Step 2: Explicit formula. The straight partial fraction decomposition will not give a nice formula because of the complex poles we saw above. However, there is a neat trick to compute the Taylor series of this kind of rational function: consolidate the denominator factors into one simple denominator, balancing with a polynomial in the numerator.
We use the identity 1 − zk = (1−z) (1 + z + z2 + ⋯ + zk−1), so that 1⁄(1−z) = (1+z+z2+⋯+zk−1)⁄(1−zk) . Hence:f(x) = 1⁄(1−x) 1⁄(1−x2) 1⁄(1−x3)
= (1+x+⋯+x5)⁄(1−x6) (1+x2+x4)⁄(1−x6) (1+x3)⁄(1−x6)
= (1+x+2x2+3x3+4x4+5x5+4x6+5x7+ 4x8+3x9+2x10+x11+x12)⁄(1−x6)3.f(x) = ∑m≥0 ((3 | m)) x6m + ∑m≥0 ((3 | m)) x6m+1 + 2 ∑m≥0 ((3 | m)) x6m+2
3 ∑m≥0 ((3 | m)) x6m+3 + 4 ∑m≥0 ((3 | m)) x6m+4 + 5 ∑m≥0 ((3 | m)) x6m+5
4 ∑m≥0 ((3 | m)) x6m+6 + 5 ∑m≥0 ((3 | m)) x6m+7 + 4 ∑m≥0 ((3 | m)) x6m+8
3 ∑m≥0 ((3 | m)) x6m+9 + 2 ∑m≥0 ((3 | m)) x6m+10 + ∑m≥0 ((3 | m)) x6m+11
+ ∑m≥0 ((3 | m)) x6m+12a6m = ((3 | m)) + 4((3 | m−1)) + ((3 | m−2))
a6m+1 = ((3 | m)) + 5((3 | m−1))
a6m+2 = 2((3 | m)) + 4((3 | m−1))
a6m+3 = 3((3 | m)) + 3((3 | m−1))
a6m+4 = 4((3 | m)) + 2((3 | m−1))
a6m+5 = 5((3 | m)) + ((3 | m−1))a6m = 3m2 + 3m + 1
a6m+1 = (m+1)(3m+1)
a6m+2 = (m+1)(3m+2)
a6m+3 = 3(m+1)2
a6m+4 = (m+1)(3m+4)
a6m+5 = (m+1)(3m+5) .a100 = (16 + 1) (3(16) + 4) = 884.
- Step 2: Recurrence.
We can clear denominators in a couple of ways, giving different recurrences.
Clearing everything:
(1−x)(1−x2)(1−x3) f(x) = 1
(1 − x − x2 + x4 + x5 − x6) ∑n≥0 anxn = 1 + 0x + 0x2 + ⋯ .
an − an−1 − an−2 + an−4 + an−5 − an−6 = 0
an = an−1 + an−2 − an−4 − an−5 + an−6 for n ≥ 1 (from a0 = 1).
(1−x2)(1−x3) f(x) = 1⁄(1−x)
(1 − x2 − x3 + x5) ∑n≥0 anxn = 1 + 1x + 1x2 + ⋯
an − an−2 − an−3 + an−5 = 1
an = an−2 + an−3 − an−5 + 1.
- Selling $100 worth of $1, $2, $3 boxes, where order matters.
- Step 0: Again, let an = number of ways to sell $n, but now order of the transactions matters.
-
Step 1: Find the generating function. Again, the outcomes have no labels 1,..., n, so we use ordinary generating functions.
We again get a choice algorithm, this time using both the Product Principle (an outcome is a sequence of independent choices, namely which kind of box sold in each transaction), along with the Sum Principle (split all outcomes into disjoint cases, depending on how many boxes in total):
Translating from logic to algebra and simplifying the geometric series:(list of k ≥ 0 boxes
of $1, $2, $3)⇔ (0 boxes) or (1 box: $1 or $2 or $3)
or ( 2 boxes: ($1 or $2 or $3) then ($1 or $2 or $3) )
or ( 3 boxes: ($1 or $2 or $3) then ($1 or $2 or $3) then ($1 or $2 or $3) )
or ⋯
f(x) = ∑n≥0 anxn = 1 + (x1 + x2 + x3) + (x1 + x2 + x3)2 + (x1 + x2 + x3)3 + ⋯
= 1⁄(1 − (x+x2+x3)) = 1⁄(1−x−x2−x3) . - Step 2: Brute force. If we only want the Taylor coefficient a100, Wolfram Alpha gives it with no trouble as the 27-digit number:
a100 = 180,396,380,815,100,901,214,157,639 that is, 180 septillion or so. (This is so much larger than the answer in Prob 1(a) because it counts the possible orderings of dozens of transactions.)
How does the computer get these coefficients so quickly (only thinking for a fraction of a second)? Let's see... - Step 2: Asymptotic formula. Wolfram Alpha gives the poles of f(x) as:
α ≈ 0.54 , β ≈ − 0.77 + 1.12i , γ ≈ − 0.77 − 1.12i ,
f(x) = 1⁄(1−x−x2−x3) = 1⁄(1 − x/α)(1 − x/β)(1 − x/γ)
= A⁄(1 − x/α) + B⁄(1 − x/β) + C⁄(1 − x/γ) .f(x) ≈ A⁄(1 − x/α) = ∑n≥0 (A⁄αn) xn ,
A = limx→α f(x) (1 − x/α) = limx→α (1 − x/α)⁄(1−x−x2−x3)
= (−1/α)⁄(−1−2α−3α2) = 1⁄α(1+2α+3α2) .
an ∼ A⁄αn = 1⁄αn+1(1+2α+3α2) .
- Step 2: Exact explicit formula. We could compute the coefficients B,C in the partial fraction decomposition the same way as A, getting an exact formula an =
A⁄αn
+
B⁄βn
+
C⁄γn
.
However, since the last two terms are small corrections in terms of the complex numbers β, γ, this is not any more useful than the asymptotic formula.
- Step 2: Recurrence. Since the denominator is an irreducible polynomial, we must clear it all:
(1−x−x2−x3) f(x) = 1
(1 − x − x2 − x3) ∑n≥0 anxn = 1 + 0x + 0x2 + ⋯ .
an − an−1 − an−2 − an−3 = 0
an = an−1 + an−2 + an−3 for n ≥ 1 (from a0 = 1).
- Step 0: Again, let an = number of ways to sell $n, but now order of the transactions matters.
- Selling $100 worth of $1, $2, $3 boxes, with order irrelevant.
- Deletion Tranform for an = # ordered sums of $1, $2, $3 with total $n. For n ≥ 1, delete the last summand: this is either 1, leaving an object of type an−1; or 2, leaving an−2, or 3, leaving an−3.
This is reversible, so a bijection.
That is, an = an−13 + an−2 + an−3 .
This is indeed the recurrence we found in Prob. 1(b).
- Ordered transactions of $1, $2, $3 with one-dollar bills marked 1,...,n. The order of bills within in each transaction also matters.
- Solve counting problem
- Step 0: Let bn be the number of ordered trnasactions with total $n in marked one-dollar bills. Since each outcome of size $n is labeled 1,...,n, we use an exponential generating function g(x) = ∑n≥0 bn xn⁄n! .
- Step 1:
We construct the appropriate exponential family. Since each transaction chooses a list of 1,2, or 3 labeled dollar bills, it can be considered as a card from the deck of directed paths of length 1,2, or 3:
D = { ① , ①→② , ②→① , ①→②→③ , ①→③→② ,
②→①→③ , ②→③→① , ③→①→② , ③→②→① }g(x) = ℓ(x) = 1⁄(1 − d(x)) = 1⁄(1−x−x2−x3) .
- We notice that the exponential generating function of bn is exactly the same as the ordinary generating function f(x) in Prob 1(b), whose coefficients an count ordered transactions with identical (unmarked) dollar bills.
This implies bn⁄n! = an , or bn = an n! .
This can be proved combinatorially by a transformation: given an ordered transaction with marked bills, consider the corresponding transaction with unmarked bills, as well as the total order of the 100 marked bills in the cash register. These two pieces of data are independent. The transformation is reversible, since any unmarked transaction shows us how to split up the list of 100 marked bills into individual transactions.
Simply put, each unmarked transaction can have n! possible orders for the marked bills.
- Solve counting problem
- Unordered transactions with marked bills.
- This is similar to 3(a). Let the number of undordered marked transactions be cn, with exponential generating function h(x). Since the order of bills in each transaction is irrelevant, the deck is now:
D = { ① , ①② , ①②③ }
h(x) = exp(x + x2⁄2! + x3⁄3!) . We can easily get the x100 coefficient by computer. It is:c100 = 11527937348312713865082241287737153907730362053400425345132475796235815534719539623297472916358562840576
- The answer c100 is actually less than 100!, and is definitely not 100! times the answer to the unmarked problem. This is because each unmarked, unordered outcome cannot be marked in 100! ways: most of these ways would count as the same, because order is mostly irrelevant.
- This is similar to 3(a). Let the number of undordered marked transactions be cn, with exponential generating function h(x). Since the order of bills in each transaction is irrelevant, the deck is now:
- Jane's Chocolate Shop sells small boxes for $1, large boxes for $2, and deluxe boxes for $3. Do a full analysis of the following counting problems, computing the generating function (ordinary or exponential), an explicit formula (if possible), a recurrence, and an asymptotic formula.
- 2/21: Midterm Exam, Friday in class. Come 5 min early for extra time.
To study:- Re-do all quizzes, covering up your previous answers, then check with my answers from class notes. Make sure you understand all mistakes. I can email you any missing quizzes on request.
- Do Midterm Review HW 2/17 & 2/19. You must actually solve these to do any good, not just read the solutions.
- Review old notes, class notes, and the Wilf text.
- Review old homework, and finish problems you didn't do.
- Come to office hours in Wells D-326: Mon, Wed 10−11 and 1−3; Thu 1−3:30 .
- Twelvefold Way and other standard sequences (Notes 1/8−1/13)
- Deletion Transforms and Recurrences (Notes 1/8)
- Enumeration Machinery (Notes 1/17)
- Ordinary generating functions for unlabeled counting (Notes 1/15)
- Exponential generating functions for labeled counting (Notes 2/3, 2/5, 2/7)
- 2/24: Trees and generating functions
HW:- As in class, let an count the number of
unlabeled ordered trees (family trees) with n vertices, and let f(x) =
∑n≥0 anxn be its ordinary generating function.
We applied the same Deletion Transform as in HW 1/13,
thinking of it as a recursive choice algorithm.
The Sum and Product Principles directly turn this algorithm into the equation:
f(x) = f(x)2 + x .
- Solve the above equation for f(x), and compare it with the generating function of the Catalan numbers. As a result, write an in terms of Cm for some m.
- For the same an, find a different recurrence coming from a different Deletion Transform. That is, remove the ancestor vertex, leaving a list of any number of smaller ordered trees. Translate this recursive choice algorithm into an equation involving f(x).
- Show that f(x) is the inverse function of g(x) = x − x2. That is, g(f(x)) = x.
- Binary trees. Recall from Quiz 4 that an unlabled ordered binary tree has an ancestor vertex at the top, and every vertex has either no children or two children (older and younger).
- Find a Deletion Transform for the binary trees, deduce an equation for the generating function f(x), and solve it to find f(x) explicitly. If possible, relate the number of binary trees to well-known numbers.
- Show that the generating function f(x) is the inverse function of g(x) = x⁄(1+x2). That is, g(f(x)) = x.
- Same as Prob 2, but for ternary trees, in which each vertex has either no children or three children (in age order). For part (b), find an appropriate function g(x) which is the inverse of f(x).
- In class, we considered rooted Cayley trees: that is, trees on a set of labeled vertices V = {1,...,n}, with some vertex designated as the root. (Identical trees with different roots count as different objects.)
- Cayley's Theorem tells the number of possible n-vertex Cayley trees without a designated root. Use this to find the number of n-vertex rooted Cayley trees.
- Give a Deletion Transform for rooted Cayley trees: a tree is equivalent to the root and a set of smaller trees. Give an equation involving the exponential generating function f(x) of rooted Cayley trees. (Why use exponential generating functions here?)
- Assume f(x) = x + x2 + a3 x3⁄3! + a4 x4⁄4! + higher terms. Substitute this into the recursive equation f(x) = x ef(x), equate coefficients of x3 and x4, and solve for a3, a4, recovering the combinatorial result of (a).
- Find a function g(x) which is the inverse function of f(x), so that g(f(x)) = x.
- As in class, let an count the number of
unlabeled ordered trees (family trees) with n vertices, and let f(x) =
∑n≥0 anxn be its ordinary generating function.
We applied the same Deletion Transform as in HW 1/13,
thinking of it as a recursive choice algorithm.
The Sum and Product Principles directly turn this algorithm into the equation:
f(x) = f(x)2 + x .
- 2/26: Lagrange Inversion Formula
Reading: Notes 2/26, Proof of the Lagrange Inversion Formula
HW:- In HW 2/24 #1−4, we got equations for several f(x), the generating functions for the number of trees of various kinds.
In each case, use Lagrange Inversion to get an explicit formula for the number of trees. Have we seen any of these answers before?
Hint: Don't use an explicit formula for the generating function f(x). Instead, use the recurrence equation for f(x) to write it as the inverse function of some simple function g(x), and apply the Lagrange Inversion Formula to find the coefficients of f(x) in terms of g(x). (Actually, it is equivalent, but easier to use the second form of Lagrange Inversion.) - Conjugal family trees.
The matriarch, Grandma Jones, lives in a house with 20 of her descendants and their spouses. Example:
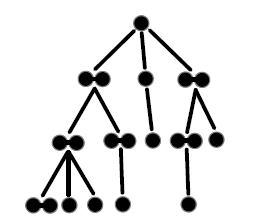
Question: How many possible family trees with 20 people?- Generalize to trees with n people. Define a Deletion Transform to get a recursive choice algorithm.
- Turn the choice algorithm into an equation involving the generating function f(x). Solve the equation to get an explicit formula for f(x).
- Use Wolfram Alpha to get the explicit answer for 20 people, using the explicit formula for f(x). Would Lagrange Inversion be effective in this case?
- Show that the generating function in this case is closely related to that for ordered trees (without considering spouses). Exactly what is the relationship?
- Same as Prob 2, but with the rule that only married spouses can have children.
- In HW 2/24 #1−4, we got equations for several f(x), the generating functions for the number of trees of various kinds.
In each case, use Lagrange Inversion to get an explicit formula for the number of trees. Have we seen any of these answers before?
- 2/28: Extra Credit Assignment: Integer Partitions.
Reading. Wikipedia on:- Integer partitions
- Euler's Pentagonal Number Theorem and Franklin's Transformation.
- The last entry in the Twelvefold Way chart is pk(n), the number of partitions of n into k parts: i.e. the surjective functions f : [n] → [k] with both [n] and [k] indistinguishable; or the ways to put n unmarked balls into k exchangeable, non-empty bins. (Here we reverse the roles of n and k from the chart, so as to have n ≥ k.)
- If we allow any number of parts, we obtain the partition number: p(n) = p≤n(n) = p1(n) + ⋯ + pn(n).
- The integer-partition numbers pk(n) and p(n) are analogous to the corresponding set-partition numbers, the Stirling number {n | k} and the Bell number B(n), which count ways to partition a set of n labeled balls.
- We usually denote partitions by writing the multiplicity of
balls in each bin, from most full to least full, using the traditional notation:
λ = (λ1, λ2,..., λk) where λ1 ≥ λ2 ≥ ⋯ ≥ λk > 0 and λ1 + λ2 + ⋯ + λk = n.
- Another useful notation is the Young diagram or Ferrars diagram of λ, in which we draw left-justified rows of dots, first a row of λi, then λ2, etc.
- For example, p(4) = 5 counts the partitions: (4), (3,1), (2,2), (2,1,1), (1,1,1,1), having Young diagrams:
• • • • • • • • • • • • • • • • • • • • - The (ordinary) generating function of the partition numbers is:
φ(x) = ∑n≥0 p(n)xn = ∏i≥1 1⁄(1−xi) .
- Euler's Pentagonal Number Theorem states that:
1⁄φ(x) = ∏i≥1 (1−xi) = 1 + ∑m≥1 (−1)m(x½m(3m−1) + x½m(3m+1)).
- We proved the Pentagonal Number Theorem by first going backward from the generating function 1⁄φ(x)
to a combinatorial model. The coefficients of ∏i≥1 (1−xi) = ∑n≥0 anxn are given by:
an = #{partitions of n into an even number of distinct parts}
− #{partitions of n into an odd number of distinct parts}. - To finish the proof of the Theorem, we gave Franklin's Transformation, which takes partitions with an even k to partitions with an odd k, and vice versa. The only exceptions are two special shapes of partitions, having m rows and n = ½m(3m−1) or ½m(3m+1) for m ≥ 1.
- Euler's Pentagonal Number Theorem
- Compute p(n) for n ≤ 10 from the Pascal-triangle-type recurrence for pk(n). (You will need to set the correct initial values on the boundaries of the triangle.)
- Prove the following recurrence from the Pentagonal Number Theorem:
p(n) = ∑m≥1 (−1)m+1(p(n − ½m(3m−1)) + p(n − ½m(3m+1))).
- Use the recurrence to compute p(n) for n ≤ 30. (Show your computations or a spreadsheet with formulas, not just the p(n) results.) Compare the efficiency with the method of part (a).
- Franklin's Transformation Proof of the Pentagonal Number Theorem.
- Illustrate Franklin's Transformation for n = 15. That is, make a table of all partitions with an even number of distinct parts, matched with the corresponding partitions with an odd number of distinct parts. There should be 27 partitions in all.
- Look up the pentagonal numbers (analogous to the triangular and square numbers). The exceptional partitions in Franklin's Transformation are those of the form:
(2m−1, 2m−2,..., m) and (2m, 2m−1,..., m+1).
- The Young diagram of (2m−1, 2m−2,..., m) is a quadrilateral. Nevertheless, give a natural, geometric correspondence between the dots in this partition and the dots in the pentagon defining the mth pentagonal number.
- Another Euler theorem: The number of partitions of n into distinct parts is equal to the number of partitions of n into odd parts.
For example, there are 8 partitions of n = 9 into distinct parts (all λi's different): (9), (8,1), (7,2), (6,3), (6,2,1), (5,4), (5,3,1), (4,3,2);
and also 8 partitions of n = 9 into odd parts (all λi's odd numbers): (9), (7,1,1), (5,3,1), (5,1,1,1,1), (3,3,3), (3,3,1,1,1), (3,1,1,1,1,1,1), (1,1,1,1,1,1,1,1,1).
- Letting an be the number of partitions of n with distinct parts, find the generating function ∑n≥0 anxn.
- Letting bn be the number of partitions of n with odd parts, find the generating function ∑n≥0 bnxn.
- Prove the generating functions in (b) and (c) are the same, by algebraic methods.
- Find a transformation of partitions which reversibly transforms partitions with distinct parts into partitions with odd parts, along with the inverse transformation going the other way.
- Theorem: The number of partitions of n with at most k parts equals the number of partitions of n whose parts are at most k.
For example, there are 5 partitions of n= 9 into at most 2 parts: (9), (8,1), (7,2), (6,3), (5,4); and there are also 5 partitions whose parts are 1 or 2: (2,2,2,2,1), (2,2,2,1,1,1), (2,2,1,1, 1,1,1), (2,1,1,1,1,1,1,1), (1,1,1,1,1,1,1,1,1).
Problem: Give a transformation proof of this Theorem.
- 3/10: Unlabeled rooted trees.
Reading:- Notes 3/10.
- Wolfram Mathworld.
- [W] Ch 1.6 pp 22−23 on the x Dlog operation.
- Tree numbers
- Use the Dlog Recurrence Formula in the Notes III.v to compute
rn, the number of distinct unlabeled, rooted, unordered trees, for n = 2,...,10,
starting from r0 = 0, r1 = 1.
That is:
rn+1 = 1⁄n ∑k=1n ∑i | k i ri rn−k+1 .
Verify the above computation by drawing all the trees for as large a size as you can. Hint: draw the possible tree shapes for a given size, and see how many distinct possible locations for the root. - We might expect that, given an unlabeled, rooted, unordered tree with n vertices, we could put labels on the vertices in n! ways,
so that we get a transformation (T, σ) ↔ L, where T is an unlabeled tree, σ is a permutation of [n], and L is a labeled, rooted, unordered tree. Based on this, we would expect:
rn n! =?? nn−1,
Why not? Explain with an example. Are there any values of n for with the equality holds? Is one side always bigger than the other?
- Use the Dlog Recurrence Formula in the Notes III.v to compute
rn, the number of distinct unlabeled, rooted, unordered trees, for n = 2,...,10,
starting from r0 = 0, r1 = 1.
That is:
- x D log method.
- Re-do HW 2/12 #2, which describes the x D log method for producing recurrences from difficult generating functions (when it is not practical to clear denominators).
- Recall from HW 2/28 that the integer-partition numbers p(n) have the generating function φ(x) = ∏i≥1 1⁄(1−xi). Use the x D log method as in Notes III to derive a recurrence for p(n). Use this recurrence to compute some values of p(n): how efficient is it compared to Euler's Pentagonal Number Recurrence?
- Extra Credit: Use the x D log method on the generating function of the Fibonacci numbers, f(x) = ∑n≥0 Fn+1xn = 1⁄(1−x−x2). Obtain a weird recurrence for Fn+1.
-
Naive recurrence for rn .
- Write the generating function of rn as: x + x2 + r3x3 + r4x4 + (higher terms), and substitute this into the generating function equation of Notes II.iv. Equate coefficients of x3 and x4 on the two sides, and solve for r3 and r4. This shows that in principle, the generating function equality can be used to determine rn .
- More systematically, expand the right side ∏i≥1
1⁄(1 − x)ri
as a product of Negative Binomials, getting a product of summations with multi-choose coefficients ((ri | ki)). Here ki ≥ 0 is the index variable of the ith summation.
Figure out which values of k1, k2,... give an exponent of xn. Equating coefficients of xn on the two sides then gives a recurrence for rn+1 as a kind of infinite convolution of multi-choose numbers.
The result is the "Naive" Recurrence Formula (since it follows unimaginatively from the generating function equality). - The above recurrence should give:
r5 = ((r1 | 4)) + ((r1 | 2)) ((r2 | 1)) + ((r2 | 2)) + ((r1 | 1)) ((r3 | 1)) + ((r4 | 1))
= 1 + 1 + 1 + 2 + 4 = 9 .M = { ® , ® , ®−−O } , which produces a 5-vertex tree T by attaching a new root to each of the roots in M:
Do this for all the other terms.T = ®−− ® −−® −−O | ®
In fact, the Naive Recurrence Formula is a direct consequence of the combinatorial recurrence: generating functions are not really needed.
- Super Extra Credit: Can you prove the Dlog Recurrence Formula for rn by a combinatorial correspondence, or in any way without generating functions? You could start by moving the denominator n to the left side, and interpreting each term as counting something, but I have no idea how to do this. Or somehow relate it to Burnside's Theorem, since that starts with 1⁄n?? This would count as original research.
Also, for 3(b):-
The recurrence is:
rn+1 = ∑k ∏i≥1 ((ri | ki)) = ∑k ((r1 | k1)) ((r2 | k2)) ((r3 | k3)) ⋯
-
Example: To compute r5, we sum over k = (4), (2,2), (1,0,1), (0,0,0,1), so that:
r5 = ((r1 | 4)) + ((r1 | 2)) ((r2 | 2)) + ((r1 | 1)) ((r3 | 1)) + ((r4 | 1)) .
- 3/12: Rooted and unrooted trees, Otter's Lemma
Reading:- Notes 3/12−3/17, I−II.
- Original paper: Richard Otter, The Number of Trees.
- Trees with n = 6 vertices
- Draw all the unrooted, unlableled, unordered trees with 6 vertices (by definition, the number of these is t6).
- For each tree, determine how many symmetries it has, and write down a few (as permutations of the vbertices, in cycle notation).
- For each tree T, determne pT, the number of distinct symmetry classes of vertices. Also determine qT, the number of symmetry classes of non-symmetric edges (i.e. edges which are not taken to themselves under any symmetry). Finally, draw T, the quotient graph (which is in fact a tree).
- Compute r6, the number of rooted, unlabeled, unordered trees, as the sum of pT for all the unrooted T.
- Find the smallest possible unlabeled tree which has no symmetries (other than the identity ε).
- Consider the following graph G, with vertices V = [18], conisisting of a 9-cycle with vertices {1,...,9}; together
with the edges 2,10 and 5,13 and 8,16; and the paths 3,11,12 and 6,14,15 and 9,17,18.
- Find the symmetries and the quotient graph of G.
- Extra Credit: Otter's Lemma says that if T is a tree, then the quotient graph T is a also a tree. Is the converse statement true? That is, if G is a graph whose quotient G is a tree, then must G also be a tree?
- Extra Credit: Prove or disprove: A tree T can never have |Sym(T)| = 3; that is, exactly 2 non-trivial symmetries.
- Trees with 6 vertices.
The trees are:
Note that T1 and T4 each have a symmetry edge in the middle (taken to itself under a reflection), which does not count in qT nor produces any edge in T.T1 T2 T3 T4 T5 T6 |Sym(T)| 2 2 2 (4)(2) = 8 3! = 6 5! = 60 pT 3 5 4 2 4 2 qT 2 4 3 1 3 1 T P3 P5 P4 P2 P4 P2 - Clearly, all the trees with ≤ 6 vertices have non-trivial symmetries. The only asymmetric tree with 7 vertices is the tree formed by joining paths P2, P3, P4 at a common end point (total 2+3+4−2 = 7 vertices).
- Symmetries and quotients of graphs
- Any symmetry must take vertices of degree d to other vertices of degree d, and it is easily seen that the only non-trivial symmetries are ±120° rotation. That is, Sym(G) = {ε, σ, σ2},
where ε is the identity and σ = (1,4,7)(2,5,8)(3,6,9)(10,13,16)(11,14,17)(12,15,18).
The quotient graph is:
12 | 10 11 | | 1 −− 2 −− 3 \ / - The quotient in (a) is not a tree, since there is an edge 13.
Also, the quotient graph of any cycle Ck is a
pathpoint. You have to think more carefully to get a non-trivial tree as the quotient of a graph with cycle.
- Any symmetry must take vertices of degree d to other vertices of degree d, and it is easily seen that the only non-trivial symmetries are ±120° rotation. That is, Sym(G) = {ε, σ, σ2},
where ε is the identity and σ = (1,4,7)(2,5,8)(3,6,9)(10,13,16)(11,14,17)(12,15,18).
The quotient graph is:
- 3/14: Rooted and unrooted trees, Otter's Lemma
Reading:- Notes 3/12−3/17, III-IV.
- Original paper: Richard Otter, The Number of Trees.
- Hand-In HW due next Fri 3/21 is announced in its own section below.
- Continuing HW 3/12 #1, consider unrooted, unlabeled trees with n = 6 vertices.
- Verify that qT = pT − 1 for each tree.
- Compute r6 = ∑T pT, the number of vertex-rooted trees, and e6 = ∑T qT, the number of edge-rooted trees, and verify that t6 = r6 − e6.
- Verify the formula from the Notes IV(v) in this case: e6 = ½[ ∑ i=15 ri r6−i − r3 ].
- Make the table of the bijection T" ↔ {T'1, T'2} which proves the above formula in the Notes IV(v). That is, T" is an edge-rooted tree, and {T'1, T'2} is a pair of non-identical vertex-rooted trees with a total of n = 6 vertices.
- Start working on the Hand-In HW due Fri 3/21.
- Give an example of a finite graph G with many edges, all of them symmetry edges. That is, for any edge, there is a graph symmetry which flips it over.
- Infinite trees. According to the Hand-In HW, a finite tree can have only one symmetry edge,
but the same is not true of infinite trees.
For each condition below, construct an infinite tree T satisfying them, or prove this is impossible.
- T has infinitely many symmetry edges.
- T has exactly one symmetry edge.
- T has exactly two symmetry edges.
Quiz 22 on Fri 3/14 was puzzling for almost everyone. I clearly underestimated the difficulty of the ideas around graph symmetry and quotients. We will have another go at this in Monday's quiz. Here is another example for you to study. Pay particular attention to the what kind of structure each object is (mapping, set, set of sets, etc.).- Consider the graph G = (V,E) with V = [7] and E = {14, 24, 34, 45, 56, 57}. That is, G is a tree with a 2-vertex stem and 3 branches on the left, two branches on the right.
- A symmetry of G is a permutation mapping σ : V to V. That is, you input a vertex to σ, and it outputs an image vertex. Each σ must take edges to edges: that is, if ij is an edge in E, then σ(i) σ(j) must also be in E.
- The symmetry group Sym(G) is the set of all symmetries (a set of mappings).
-
I will write the symmetries in cycle notation, but omitting 1-cycles. For example, σ = (132) means (132)(4)(5)(6)(7), the mapping σ(1) = 3, σ(2) = 1, σ(3) = 2, and σ(i) = i otherwise. This graph symmetry is neither a reflection nor a rotation; rather, it permutes the left branches while leaving the right branches fixed. We can check directly that σ takes edges to edges: e.g. 14 goes to σ(1) σ(4) = 34.
Sym(G) = { ε, (12), (13), (23), (123), (132), (67), (12)(67), (13)(67), (23)(67), (123)(67), (132)(67) }
-
To define the quotient graph G− = (V−,E−), we must define its vertices and edges. A vertex x− of G− is a symmetry class of vertices. That is, x− is a set of vertices of G: x− = {σ(x) for all σ ∈ Sym(G)}.
V− is the set of all the different x− (thus, V− is a set of sets).
V− = {1−, 4−, 5−, 6−}, where 1− = {1,2,3}, 4− = {4}, 5− = {5}, 6− = {6,7}.
- Next, two distinct vertices x−, y− form an edge x−y− in E− whenever there is an edge of G between elements of x− and y−: i.e. when x'y' in E with x' in x− and y' in y−. (Thanks to Riley for this simple definition.) E− = {1−4−, 4−5−, 5−6−}, so G− is a path on 4 vertices.
- 3/17: Finish tree enumeration
Reading:- Hand-In HW due Fri 3/21 is announced in its own section below.
- Notes 3/12−3/17: Note especially the proofs in III, which I revised.
- Math 880 Notes on Tree Asymptotics. See how this subject continues at a graduate level.
- Analytic Combinatorics by Flajolet and Sedgewick. An encyclopedic textbook of all aspects of enumeration, especially asymptotic formulas via complex analysis. Their motto: "If you can specify it, you can count it."
- Compute some unrooted tree-numbers tn, using the known rooted numbers rn from HW 3/10 #1a, and the Otter's Formula in the Notes IV(v). Compare to the values at the Online Encyclopedia of Integer Sequences (#A000055 and #A000081).
- Work on the Hand-In HW due Fri 3/21.
- Hand-In HW due Fri 3/21.
Prove the following:
Hints:Proposition: Any finite tree T has at most one symmetry edge. - Recall that a symmetry edge of a (finite simple) graph G = (V,E) is e = vw such that v = σ(w) for some symmetry σ ∈ Sym(G). (See Notes 3/12−3/17 II(ii) and II(iii)(c).)
- Experiment by trying to construct a counter-example, a tree with two or more symmetry edges. What prevents this from working? Compare with HW 3/14 #3 & 4.
- The Proof Notes from Math 481, give basic tips on style and content of proofs.
- As a basis for your proof, start from the definitions and theorems in the Graph Notes from Math 481 (only parts I & II are relevant). You may also use the HHM textbook, especially Ch. 1.1.2, p. 5 and Ch. 1.3, p. 30. You may quote and use any of the results in these references.
- You may also quote and use the Claims (i)−(iv)
in the Solutions 3/14 #4(c). This problem proves that exactly 2 symmetry edges are impossible, whereas you must prove this for ≥ 2 symmetry edges.
Note: My proof is pretty involved, so do not just try to extend it. The theorem you are proving is actually easier, because it involves only finite graphs. - Show that removing a symmetry edge e from T leaves two disjoint identical trees related by a symmetry, each having half the vertices of T. If there were another symmetry edge e', it would have all the same properties as the original e. Where could e' be, relative to e?
- The proof will be worth 9 points = 3 quizzes.
- Hand in the first draft on 3/21, and when I hand back corrections, you can incorporate them into a second draft for more credit.
- Hand-In HW due Fri 3/28. Second draft of your proof from last week.
- The top scores on the first draft were 6/9pts. The second draft will raise your score toward the maximum 9/9pts.
Re-submit the first draft together with the second. - Address all corrections and issues raised in my comments.
- Write clear paragraphs, each stating and reaching some logical goal (e.g. a claim or lemma).
- Omit every word that does not advance the logic toward the conclusion. In particular, the proof should not contain examples, since these cannot prove general statements: put examples in a note before or after the proof.
- A schematic picture can help you and your reader keep track of the argument (but does not substitute for the argument, of course).
- Make sure you explicitly use the properties of a tree (connected, acyclic). Ask: would your argument work just as well for any graph G? If not, exactly where does it use the tree properties? Give explicit references to previously known results whenever used.
- Given a symmetry edge e = σ(e), then any other symmetry τ takes e to some other symmetry edge, but there is no immediate reason to deduce τ(e) = e. This would be obvious only if e were the unique symmetry edge (which is what you are trying to prove).
- Here is a good notation which should clarify your arguments.
- For a graph G, let Gx denote the connected component of the vertex x: the subgraph of all vertices y connected to x by paths in G, and all edges yy' in G between such vertices. We also have Gx = Gy for any y ∈ Gx .
- Thus, for a tree T with distinct edges e = xy, f = vw, we have the connected components:
T−e = (T−e)x ∪ (T−e)y
T−f = (T−f)v ∪ (T−f)w - Also, if we remove both edges, we get components:
(T−e−f)x, (T−e−f)y,
(T−e−f)v, (T−e−f)w.
However, T−e−f has only 3 distinct components, so two of these must be the same;
by switching labels, we may assume that (T−e−f)x = (T−e−f)w, so that:
T−e−f = (T−e−f)v ∪ (T−e−f)x ∪ (T−e−f)y = (T−e−f)v ∪ (T−e−f)w ∪ (T−e−f)y. - The key point in one proof-strategy is to show something like (T−f)v ⊂ (T−e)x, or (T−e)x = (T−f)v ∪ (T−e−f)w, or (T−e)y ⊂ (T−f)w. Show such statements from their definitions and the basic properties of trees. Any such statement should lead very quickly to a contradiction, since if e, f are symmetry edges, then each component of T−e or of T−f contains exactly half the vertices of T.
- Another proof strategy involves the set of symmetry edges S in T: we can define edges e,f ∈ S to be adjacent if there is a path from e to f in T containing no other symmetry edge.
This makes S into vertices of a graph (that is, the elements of S are edges of T, but count as vertices of the derived graph T~). Show explicitly that this graph T~ is a tree, or some similar statement.
Another way to set up T~ would be as a bipartite graph, having vertices of two kinds: V = S ∪ C, where S is the set of all symmetry edges of T, and C is the set of components of T−S (removing all symmetry edges, but not their end-points). The edges of T~ are pairs of the form ec, where the component c contains an end-point of symmetry edge e.
- The top scores on the first draft were 6/9pts. The second draft will raise your score toward the maximum 9/9pts.
- 3/19: Start on polyhedra.
Reading:- Wikipedia on polyhedra, Platonic solids, and Archimedean solids.
- Graph Notes from Math 481, including Planar Graphs (III) and Polyhedra (IV).
- Consider the following standard polyhedra discussed in class, and illustrated in Wikipedia:
cube, octahedron, pyramids, prisms, anti-prisms, and vertex-truncations of these.
- Practice drawing the above polyhedra in a legible way, clearly showing the vertices, edges, and faces.
- Draw the edge-graphs of the above polyhedra, as graphs without edge-crossings.
- Determine the dual polyhedra of the above examples.
- Work on the Hand-In Proof due next time.
- Standard polyhedra.
- Drawings and edge-graphs of the regular polyhedra (Platonic solids) are on [HHM] Ch. 1.5.3 p. 82. These polyhedra are dual to each other: the cube and the octahedron; the tetrahedron with itself; the dodecahedron and the icosahedron.
- The edge-graph of a pyramid is a wheel graph: a cycle with an extra vertex in the middle and spoke-edges. The dual polyhedron is the same pyramid (upside-down).
- The edge-graph of a polygonal prism is a double cycle with edges between corresponding pairs of vertices. The dual polyhedron is a bipyramid.
- The edge-graph of an anti-prism is a double cycle with zigzag edges in between. The dual polyhedron is a trapezohedron.
- The effect of a vertex truncation on the edge-graph is to replace the truncated degree-d vertex with a d-cycle of degree-3 vertices. The effect on the dual polyhedron is to add an extra vertex slightly beyond the face corresponding to the truncated vertex; i.e. gluing a polygonal pyramid onto that face.
- 3/21: Vertex and face constructions of polyhedra.
Reading:- Notes on dot and cross product of vectors.
- Video tutorials on dot and cross product.
- For a given vector a and constant c, a line in the plane can be defined as:
La,c = {x ∈ R2 s.t. a • x = c}.
(a, c) = ((1,1), 2), ((-1,1), 2), (−1,2), 0).
- The 3 lines have 3 pairwise intersection points. Find these points by solving a pair of equations a • x = c.
- The 3 lines cut out 7 regions of the plane. Find the relations of the form a • x ≤ c or a • x ≥ c which define each region.
- There are 8 possible choices of "≤" or "≥" for the 3 values of (a, c), but only 7 regions. What set does the extra choice define?
- If we did the same exercise for 4 vectors in R3, how many regions would we get? What would be the shape of the bounded region?
- Constructions of polyhedra
- Consider the tetrahedron with vertices:
(0,0,0), (1,1,1), (1,2,3), (−1,1,1).
- Find the center of gravity of the tetrahedron.
- Find the relations for a polyhedron obtained by slicing off a small part of the corner near (1,2,3). (You decide the slicing plane and how much to cut off.) What is the name of the resulting polyhedron?
- Find the vertices of your sliced polyhedron in (c).
- Find the relations for a polyhedron obtained from the tetrahedron by adding a new vertex a little above the triangular face with corners (0,0,0), (1,1,1), (1,2,3). (You pick the vertex.) What is the name of the resulting polyhedron?
- Consider the tetrahedron with vertices:
- 3/24: f-vectors of polyhedra: (n,q,r)
Reading:- Euler's Formula, from Martin Aigner & Günter Ziegler, Proofs from THE BOOK
- Notes: Günter Ziegler, Convex Polytopes: Extremal Constructions and f-Vector Shapes
- Dual-tree proof of Euler's Formula (see Aigner & Ziegler). Let P be the polyhedron obtained from the octahedron by truncating a vertex.
- Draw a Schlegel diagram of P: i.e. a planar drawing of the edge-graph G, obtained from projecting P from a point beyond one of the faces onto a screen on the far side.
Hint: Draw the usual edge-graph of the octahedron (4 triangles at each vertex), and modify it by the cut-off corner. Or try to picture the Schlegel projection. - Using another color, superimpose the dual graph G*: in each region Ri of G, draw a vertex vi* of G*; and whenever two regions Ri, Rj of G are adjacent, draw an edge vi*vj* of G*. Note that each vertex of G corresponds to a region of G*.
- Draw a spanning tree T ⊂ G: i.e. a tree connecting all the vertices of G.
- Draw the subgraph T* ⊂ G* containing all vertices of vi* and all edges vi*vj* which do not cross any edge of the tree T in (c).
- Explain why T* must be connected and acyclic, given that T is acyclic and connected.
- Without counting, find the number of edges q
in G as the number of edges of T plus the number of edges in T*:
q = (n−1) + (r−1), where G has n vertices and G* has r vertices. Explain why this is equivalent to Euler's Formula.
- Draw a Schlegel diagram of P: i.e. a planar drawing of the edge-graph G, obtained from projecting P from a point beyond one of the faces onto a screen on the far side.
-
The f-vector of a polyhedron is the triple
(n,q,r) of its vertex, edge, and face numbers.
Since q = n + r − 2, it is enough to record (n,r).
In the next lecture, we will prove
Steinitz's Lemma: For any polyhedron P, we have:½ n + 2 ≤ r ≤ 2n − 4.
- In the (n,r) plane, draw the wedge region defined by the above inequalities, and mark the integer points in this region. These are the f-vectors of all possible polyhedra P.
- For all the standard polyhedra in HW 3/19 #1, including Platonic solids, pyramids and bipyramids, prisms and anti-prisms, compute the f-vector (n,r), and plot it in the above region. (Include some truncations and multiple truncations.)
- What distinguishes the polyhedra whose f-vector lies on the upper boundary of the (n,r) region? What about the lower boundary?
- Can you find polyhedra whose f-vectors give all the (n,r) in your picture (up to some bound on n and r)?
- Work on the second draft of your proof from last week. See the hints below.
- Extra Credit: Show that every polyhedron has a triangle face, or a simple vertex (a vertex of degree 3), or both. Even stronger, show that the number of triangle faces plus the number of simple vertices is at least 8, so there are at least 4 triangle faces, or at least 4 simple vertices. Hint: Use Euler's Formula, and the Edge-Vertex and Edge-Region Formulas. (From Ziegler p. 24.)
- Here are two drawings of the edge-graph G of the vertex-truncated octahedron: the upper right drawing is a Schlegel projection from the indicated light source; the lower one is the standard drawing for the octahedron, with the top vertex expanded into a 4-cycle. In each drawing, a spanning tree T of G is traced in green, the dual spanning tree T* of G* is in red.
Clearly, every edge of G is either green, or has a red edge crossing it, so the number of edges of G equals the numbers of edges of T and T*: thus, q = (n−1) + (r−1); in this case, q = (9−1) + (9−1) = 16. - Steinitz Lemma
- The set of f-vectors (n,r) of polyhedra makes the following cone in the plane:
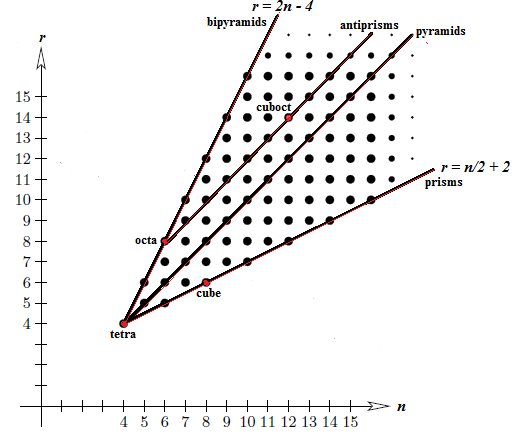
- The picture above is marked in red with the f-vectors of various polyhedra.
- The top line r = 2n − 4 corresponds to "simplicial polyhedra", those whose faces are all triangular and whose edge-graphs are maximal planar. The bottom line corresponds to the "simple polyhedra", the duals of simplicial, whose corners all have 3 edges.
- We can construct polyhedra with all vectors in the cone. We start with prisms, which give all vertices on the diagonal r = n. Performing truncation at a vertex with 3 edges changes (n,r) to (n+2, r+1); and we can repeat such truncation indefinitely, since every vertex of the new face has 3 edges: this fills the top half of the region (above r = n). Taking dual polyhedra then fills the bottom half. Alternatively, repeatedly stack a pyramid onto a triangular face, changing (n,r) to (n+1, r+2).
- The set of f-vectors (n,r) of polyhedra makes the following cone in the plane:
- 3/26: Steinitz's Lemma and Steinitz's Theorem
Reading:- Notes 3/26−3/28
- Survey: Günter Ziegler, Convex Polytopes: Extremal Constructions and f-Vector Shapes
- Connectivity, 3-connected graphs: R. Diestel, Graph Theory, 4th ed., p.10 and p.62
- Maximal planar graphs (equivalent to triangular polyhedra): Math 481 Graph Notes III.8 and HW 11/15 #3, HW 11/18 #4.
- A triangular polyhedron means one with only triangular faces.
- Use Euler's Formula and the Edge-Region formula ∑R deg(R) = 2q to show that a polyhedron is triangular if and only if it has n vertices, q = 3n−6 edges, and r = 2n−4 vertices. (This numerical condition means (n,r) lies on the upper edge of the Steinitz region, the wedge in the (n,r) plane containing all possible f-vectors.)
- Find two maximal planar graphs with (n,r) = (6,8), but which are combinatorially inequivalent. Draw polyhedra associated to these graphs.
Hint: One is the edge-graph of a standard polyhedron. The other graph is made from two 3-cycles connected in a non-standard way.
- Combinatorial types with f-vector (7,7).
Consider the following graph: G is a 5-cycle C5 with consecutive vertices 1,2,3,4,5; and inside the cycle is vertex 6 adjacent to 1,2,3,7; and vertex 7 adjacent to 1,4,5,6.- Find a standard polyhedron with (n,r) = (7,7).
- Show the above graph G is planar and 3-connected with (n,r) = (7,7); but it is not isomorphic to the graph from part (a). Hence G is the edge-graph of a polyhedron combinatorially inequivalent to the one from (a).
- Draw a sketch of a polyhedron having edge-graph G.
- Find a third inequivalent graph and polyhedron with (n,r) = (7,7), by modifying the construction of G.
- Cyclic polyhedron
- For any n ≥ 4, the cyclic polyhedron (usually called the cyclic polytope) P = Cyc(n) is a weird oyster-shape (Ziegler Fig 1.2) which is the convex hull of n vertices: pick any real numbers t1 < ⋯ < tn, and define: vi = (ti, ti2, ti3). That is, the vertices are points on the rational normal curve c(t) = (t, t2, t3).
- The convex hull of these vertices is the n-vertex cyclic polyhedron Cyc(n).
- It is known that the faces of Cyc(n) are the triangles with vertices vivjvk, where j = i+1 or k = j+1.
- Here is another picture:

- Verify the description of the faces in the two pictures.
- Determine the number of faces and edges for Cyc(n). (Why was this predictable?)
- Make a planar drawing of the edge-graph of Cyc(n).
- Unique polyhedra
- Prove that any polyhedron with (n,r) = (4,4) is combinatorially equivalent to the tetrahedron.
- Draw the (combinatorially unique) polyhedron with (n,r) = (5,6); and its dual with (n,r) = (6,5).
- Convince yourself that all of the above edge-graphs are 3-connected: that is, removing any 2 vertices leaves the graph connected.
- Work on the second draft of your proof from last week. See the hints below.
- 3/28: Balinski's Theorem:
Edge-graph of P is 3-connected.
Reading:- Notes 3/26−3/28
- Wikipedia. This proof of the Theorem is similar to the one I gave in class.
- I adapted my presentation from Günter Ziegler, Lectures on Polytopes, p. 95.
- Can you identify the polyhedron in Dürer's famous picture Melencolia, in terms of our standard polyhedra, their duals, and our construction methods?
(Try enlarging for a better view. The shape has a small triangle on top and bottom, and 3+3 non-regular pentagonal sides. It is sort of a triangular version of the dodecahedron.)
Hint: The dual is a polyhedron which is fairly easy to visualize.

- Balinski Proof.
- Balinski's Theorem (for dimension 3): The edge-graph G of a convex 3-dimensional polyhedron P is 3-connected. That is, G−v1−v2, the graph with any two vertices removed, is always a connected graph.
- Case (i): Suppose v1 and v2 lie on a face F of P. Suppose that, for a normal vector a, the plane of F is given by the equation a • x = c, so that a • x ≤ c for all x ∈ P. The "height" function a • x has a maximum value a • x = c for x on F, and a minimum value a • x = b for x in some "bottom" flat B (a vertex, edge, or face).
Now, any vertex v ∉ B has a lower neighbor w, meaning a • w < a • v : this is because P contains points lower than v by hypothesis, and P is contained in the cone of v, whose edges are the neighbors of v. Therefore, we can connect v to the bottom B by a strictly decreasing path, which cannot contain v1 or v2 since the path contains at most one point with a • x = c. Thus, any two vertices v, v' can be connected to each other in G−v1−v2 by connecting v to some w ∈ B and v' to some w' ∈ B, and connecting w to w' along the edge-graph of B (which is a vertex, an edge, or a cycle). - Case (ii): Suppose v1 and v2 pass through the interior of P. Then we can take a third vertex v0, so that v0, v1, v2 define a plane, a • x = c. By the same reasoning as before, for any vertex v with a • v ≤ c, we can connect v by a downward path to the "back flat" B = {x such that a • x = min}. Also, for any vertex v with a • v ≥ c, there is an upward path to the "front flat" F = {x such that a • x = max}. Finally, the middle vertex v0 connects to both F and B, so we can clearly produce the needed paths in G−v1−v2.
- Let v1 = (½, ½, 3⁄2) and v2 = (1,1,1). These lie in the triangular face with vertices v1, v2, and v0 = (1,0,1). Illustrate Case (i) above by computing a normal vector a to this face, and marking all vertices v with their height in the direction a, that is a • v. (Hint: You can scale a to any convenient length.) Verify that every vertex in G−v1−v2 can be connected by a decreasing path within G−v1−v2 to the "bottom flat" B (the points x ∈ P where a • takes on its minimal value). Show how this connects any two vertices.
- Now let v1 = (½, ½, 3⁄2) and v2 = (1,0,0). Pick another vertex v0 = (0,0,0). Illustrate Case (ii) above by computing a normal vector to the plane containing v0, v1, v2, and marking all v with their a-height. Verify that every v on or below the plane can be connected by a decreasing path to the "back flat" B (the points of minimum a-height); and every v on or above the plane can be connected by an increasing path to the "front flat" F (the points of maximum a-height). Also, v0 can be connected to both B and F. Show how to connect any two vertices in G−v1−v2 by concatenating these paths.
- The dual of a k-gon anti-prism is a k-gon trapezohedron. The pictured solid is a triangular trapezohedron, with the top and bottom vertices truncated. Thus, the solid is the dual of a triangular anti-prism (an octahedron), with small triangular pyramids stacked on top and bottom.
- Balinski proof
-
Find the normal vector a by taking the cross-product (v1−v0) × (v2−v0), and scaling to clear denominators. The "heights" a • v are in green.
We consider "up" and "down" relative to the direction a, not the vertical direction.
- Similar to (a).
-
Find the normal vector a by taking the cross-product (v1−v0) × (v2−v0), and scaling to clear denominators. The "heights" a • v are in green.
We consider "up" and "down" relative to the direction a, not the vertical direction.
- 3/31: Augmenting path algorithm
Menger's Theorem: Minimum number of disconnecting points = maximum number of connecting paths
Reading:- Notes 3/31
- I adapted my proof from Diestel, Graph Theory, p. 68−71.
- Generalization: independent paths are a special case of flows, and the augmenting path algorithm finds a maximum flow.
- Determine the connectivity index κ(G) for the following edge-graphs of the following polyhedra.
Also, compare with the minimum vertex-degree δ(G) = min{deg(v) for v ∈ V}.
(We always have κ(G) ≤ δ(G), since we can always remove all the neighbors of a vertex to isolate it, disconnecting the graph.)
- Each of our standard polyhedra from HW 3/19 #1.
- The k-gonal prism with pyramids stacked on the top and bottom k-gons
- Two triangular anti-prisms glued top-to-bottom. In the Schlegel diagram below, there are three triangular shells (exterior, intermediate, interior) corresponding to the tops and bottoms of the anti-prisms.
- Extra Credit: We know by Graph Notes III.9 that any polyhedron graph G (in fact any planar graph) has a vertex of degree at most 5; and G is 3-connected by Balinski's Theorem. Thus:
3 ≤ κ(G) ≤ δ(G) ≤ 5.
-
Consider the 4 × 4 grid graph G whose vertices are the integer points V = {(i,j) with i,j = 0,1,2,3};
with edges of the form e = (i,j)(i,j+1) or (i,j)(i+1,j) for all i,j. Let x = (0,1) and y = (3,2), and ℘ = {P1, P2}, the family of two "greedy" paths which connect x and y in the shortest way:
P1 = (0,1)(0,2),(1,2),(2,2),(3,2) and P2 = (0,1),(1,1),(2,1),(3,1)(3,2).
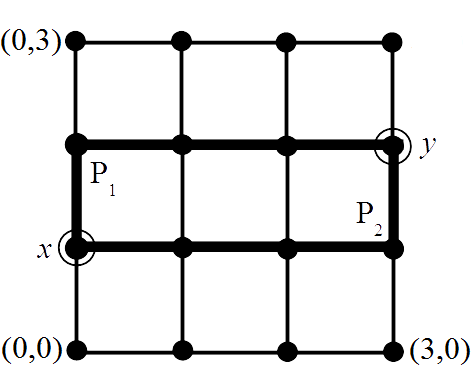
- Apply the Augmenting Path Algorithm to modify the above paths ℘, into a family ℘' of 3 independent xy-paths.
- Apply the algorithm one more time to find a disconnecting set {v1, v2, v3}.
- What is the connectivity κ(G)? How can you be sure?
- Same as the previous for the following example:
Let x = (1,1) and y = (0,2), and ℘ = {P1, P2} with:
P1 = (1,1)(2,1),(3,1),(3,0),(2,0) and P2 = (1,1),(0,1),(0,2).
- Connectivity index
- Standard polyhedra: Each polyhedron family is over a k-gon. We compare the connectivity index κ(G) to the minimum vertex degree δ(G) = min{deg(v) for v ∈ V}.
Exception: Bipyr(3) has κ(G) = δ(G) = 3.P pyram prism anti-pr bipyr trapezo dodeca icosa κ(G) 3 3 4 4 3 3 5 δ(G) 3 3 4 4 3 3 5 - For P = k-prism with k-pyramids stacked on top and bottom, we have κ(G) = δ(G) = 4 for k ≥ 4, and κ(G) = δ(G) = 3 for k = 3.
- The 3 vertices of with deg(v) = 6 form a cut-set,
and we can find 3 paths between any two vertices, so κ(G) = 3. But δ(G) = 4,
so in this case κ(G) < δ(G).
- Standard polyhedra: Each polyhedron family is over a k-gon. We compare the connectivity index κ(G) to the minimum vertex degree δ(G) = min{deg(v) for v ∈ V}.
- Augmenting paths on the 4×4 grid graph G.
- Below left is one possible augmenting path Q in red, traversing two backward edges of ℘ = {P1, P2}. Erasing the backward edges (below right) unblocks the third xy-path, producing the modified path family ℘' = {P1', P2', P3'}.
- The red vertices in the picture above right give the cut-set produced in Case (ii) of the Algorithm. For this graph, we have κxy(G) = deg(x) = 3, and the xy-paths use all the edges at x. No more augmenting paths are possible except the 1-point path of x itself, and the cut-set chooses the second vertex on each path, the neighbors of x. (If there do exist augmenting paths, we define vi to be the farthest vertex on Pi reachable by such a path.)
- The above guarantees that κxy(G) = 3. If we ran the Algorithm for all pairs x,y, it would show that κ(G) = min{κxy(G) for all x,y} = 2. We can see this informally by imagining 2 independent paths between any two vertices, including the corners with deg(v) = 2.
- Below left is one possible augmenting path Q in red, traversing two backward edges of ℘ = {P1, P2}. Erasing the backward edges (below right) unblocks the third xy-path, producing the modified path family ℘' = {P1', P2', P3'}.
- 4/2: Classifying polyhedra
Reading:- Wolfram Mathworld on polyhedral graphs and hexahedra, and Wikipedia on hexahedra. (6-faced polyhedra)
- Numericana on enumerating polyhedra. This chart shows how many combinatorial types correspond to each f-vector (n,r) in the Steinitz region.
- Constructing 3-connected graphs: Diestel Ch. 3.2, p. 68 after Thm 3.2.3.
- Extra reading: Edward Bender, The number of three-dimensional convex polyhedra. This is a difficult counting problem that can be handled by methods similar to the unlabeled trees (but harder). It again shows the tremendous power of generating function methods.
- A theorem of Tutte states that every 3-connected graph can be constructed from the tetrahedron Pyr(3) by drawing extra edges
between existing vertices, between midpoints of existing edges, or one of each.
Examples:
- We get Pyr(4) from Pyr(3) by adding a vertex at the midpoint of one of the exterior edges, and drawing an edge from the new vertex to the center.
- We get a 6-vertex polyhedron by drawing an edge between the midpoints of two edges of Pyr(3).
- All polyhedra with 5 vertices. How many are there?
- All polyhedra with 6 vertices. Seven combinatorially distinct ones are possible, distinguished by their lists of vertex degrees:
(deg(v1),..., deg(v6)) = (3,3,3,3,3,3), (3,3,3,3,3,5), (3,3,3,3,4,4),
(3,3,3,4,4,5), (3,3,4,4,4,4), (3,3,4,4,5,5), (4,4,4,4,4,4).
- Pictures
- Dualize the graphs in #1 to get all the pentahedra (5 faces) and hexahedra (6 faces).
- Draw legible pictures of each polyhedron in (a).
- There is one hexahedron with 4 triangular and 2 quadrilateral faces. It is the smallest polyhedron with chirality: no stretched version of it is equivalent by rotation to its mirror image, so it inevitably has left- and right-handed versions. Draw these.
- We apply the construction algorithm described in the problem to produce all possible 5-vertex polyhedral graphs.
- Starting with the tetrahedron graph Pyr(3) we subdivide one edge to introduce a fifth vertex. (Since all edges are symmetric to each other, it does not matter which edge.) This new vertex is one end of a new edge, and if we want exactly 5 vertices, the other end must be an existing vertex.
- We cannot create any more vertices (having 5 already), so we can only connect the two existing vertices across the single face which is not a triangle (the outer region in the picture). The result is a maximal planar graph (all regions triangles), so we cannot add any more edges.
- Mathworld also has the geometric hexahedra. (Note the confusing terminology: the "hexahedral graphs" have 6 vertices, whereas the geometric hexahedra have six faces.) The left and right versions of the chiral hexahedron are shown on Wikipedia and Numerica (the "tetragonal antiwedge").
- 4/4: Properties of polyhedral graphs. Start Rubber-Band Model.
For the next couple of weeks, we will study the proof of Steinitz's Theorem which combines ideas from the graph-theorist Tutte and the physicist Maxwell.
Reading:- Again review Graph Notes from Math 481, including Planar Graphs (III) and Polyhedra (IV).
- Khan Academy on Hooke's Law and potential energy; and on line integrals.
- Steinitz Proof: Jurgen Richter-Gebert, Realization Spaces of Polytopes, pp. 120−143.
- Basic formulas for polyhedral graphs with n vertices, q edges, and r regions:
- Vertices have deg(v) ≥ 3; edges adjoin 2 distinct regions; regions have deg(R) ≥ 3.
- Edge-Vertex & Edge-Region: ∑v deg(v) = 2q ; ∑R deg(R) = 2q.
- Euler: n − q + r = 2.
- q ≤ 3r − 6.
- n ≤ 2r − 4 (one of Steinitz's inequalities).
- There is some region with deg(R) ≤ 5; that is, every polyhedron has some face which is a triangle, quadrilateral, or pentagon.
- Potential energy
- Recall that, given the force F(x) along the x-axis, the potential energy (the amount of work needed to reach a given point x1 from the origin) is the integral:
PE(x1) = −∫0x1F(x) dx .
- If we have two Hooke forces pulling toward different centers:
F(x) = −(x−a1) − (x−a2),
- Show that no matter how many Hooke forces we add, the potential has a unique minimum point x = x0, which is the unique equilibrium point: all the forces cancel, giving F(x0) = 0.
- Recall that, given the force F(x) along the x-axis, the potential energy (the amount of work needed to reach a given point x1 from the origin) is the integral:
- Generalize Prob 2 to two dimensions. The vector force field F(x,y) = −(x,y) has potential energy given by a line integral
PE(x1,y1) = −∮ F(r) • dr ,
-
Compute the potential for the two-dimensional Hooke force field above.
Hint: Use a radial path r(t) = (tx1,ty1) for 0 ≤ t ≤ 1. - Extra Credit: Why is this a conservative field?
- Again show that no matter how many Hooke forces we add, the potential has a unique minimum point which is the unique equilibrium point.
-
Compute the potential for the two-dimensional Hooke force field above.
- 4/7: Rubber-Band Model.
Reading:- Notes corrected
- Steinitz Proof: Richter-Gebert pp. 123−124.
- Web notes on Gaussian elimination.
- We will find the equilibrium position for the familiar graph:
- Write appropriate coordinates to record the positions of the mobile vertices v1, while the outer v3, v4, v5 are fixed in convenient positions − not necessarily an equilateral triangle.
- Write the forces F1, F2 (vector functions depending on the positions of v1, v2) acting on the mobile vertices v1, v2.
- Solve a system of linear equations to find the equilibrium points.
- Compute the potential function PE, which represents the work performed against the force when we start with v1, v2 both at (0,0), we move v1 to its given position, then move v2 to its position.
- Why is it clear that PE has a large positive value whenever v1 or v2 are far from the origin? What does this mean about the critical points of PE?
- Show that the critical points with ∇PE = (0,...,0) are precisely the equilibrium points of F1,..., F5.
- Same as #1, but for the chiral hexahedron graph:
- 4/9: Rubber-Band Model.
Reading:- MathWorld on the Incidence Matrix.
- Steinitz Proof: Richter-Gebert pp. 123−124.
- Extra Credit: Hand in the answer to HW 4/7 #2. That is, find the
equilibrium position for the chiral hexahedron graph:

Next lecture, I will compare your results to a rubber-band experiment.
Try some other interesting graphs, such as the Platonic graphs. For example, for the octahedron graph, how much smaller is the internal triangle than the external? I would be impressed if you write some software for this.
- 4/11: Finish Rubber-Band Model.
Reading:- Example: of the equilibrium computation using incidence matrices (a readable part of Richter-Gebert, p. 138).
- Check out Sam Moore's brilliant rubber-band app!
Controls:- Click and drag any vertex to move.
- Right click a vertex to toggle whether it is fixed or mobile.
- Add vertex and delete vertex.
- Set edge toggles to & from edge mode, where you click on two vertices to create an edge between them.
- Wikipedia on Laplacian matrix and algebraic connectivity.
- Partial Laplacian matrix
- For a graph G = (V,E) with vertices V = {1,...,n}, we denote the position of a vertex by vi = (xi, yi).
We designate an external cycle with vertices vk+1,..., vn, and pin them in
fixed positions;
while we allow the internal vertices v1,..., vk to move to arbitrary positions.
An equilibrium position makes the rubber-band forces cancel at each internal vertex:
Fi = ∑j ∈ N(i) (vj − vi) = (0, 0) for i = 1,...,k,
- We now give another way of setting up this linear system of equations.
Define a k×k matrix, called the partial graph Laplacian, L = (ℓij), whose entry in row i, column j is:
Let x = (x1,..., xk) and y = (y1,..., yk) be k×1 column-vectors of variables (coordinates of internal vertices). Finally, define b = (b1,..., bk) and c = (c1,..., ck) by:deg(vi) if i = j, ℓij = −1 if ij ∈ E 0 otherwise. bi = ∑j ∈ XN(i) xj , ci = −∑j ∈ XN(i) yj ,
- Show that v1,..., vk defines an equilibrium position exactly when:
L • x = b and L • y = c,
- Consider the graphs in HW 4/7 #1,2. Use Wolfram Alpha to do Gaussian elimination (row-reduction) on the matrix L, augmented by the constant vectors b and c, and find the equilibrium position. (Command: row reduce {{1,2,3},{4,5,6}} for the 2×3 matrix with rows (1,2,3) and (4,5,6).)
- Extra Credit: Same as (b) for the icosahedron graph.
- For a graph G = (V,E) with vertices V = {1,...,n}, we denote the position of a vertex by vi = (xi, yi).
We designate an external cycle with vertices vk+1,..., vn, and pin them in
fixed positions;
while we allow the internal vertices v1,..., vk to move to arbitrary positions.
An equilibrium position makes the rubber-band forces cancel at each internal vertex:
- Full Laplacian matrix
- Continuing with the graph G with n vertices from Prob 1, the adjacency matrix is the n×n matrix A = (aij) whose entry n row i, column j is aij = 1 if ij ∈ E, and aij = 0 otherwise. This is an obvious book-keeping device for the edges and vertices of G: what is amazing is that considering it as a matrix with eigenvalues, etc., gives subtle information about the graph.
- The (full or ordinary) Laplacian of a graph G is the matrix L = D − A, where D is the diagonal matrix with deg(i) in the (i,i) position (and 0 elsewhere). (Thus, the full Laplacian L = (ℓij) has the same entries as in Prob 1, except that it is for all n vertices, not just the mobile vertices 1,...,k.)
- The Laplacian always has an eigenvalue λ = 0: that is the n×1 column vector u1 = (1,...,1) satisfies L • u1 = 0 u1 = (0,...,0). Furthermore, it is known that L is diagonalizable with n non-negative eigenvalues 0 = λ1 ≤ λ2 ≤ ⋯ ≤ λn.
- The second eigenvalue λ2 is known as the algebraic connectivity. We have λ2 ≥ 1 if and only if G is connected; and in general, it gives a lower bound for the usual index of connectivity: λ2 ≤ κ(G). (Recall that κ(G) is the minimum number of vertices whose removal disconnect the graph, and this can be computed by the Augmenting Path Algorithm applied to all pairs of vertices.) There are many other results in spectral graph theory, relating the eigenvalues (or spectrum) of L with graph-theory properties of G.
- Let G be the 5-vertex graph in HW 4/7 #1. Write its 5×5 adjacency matrix A and its 5×5 (full) Laplacian L = D − A.
- For the same G, find the spectrum (set of eigenvalues) of L on Wolfram Alpha. (Example: eigenvalues {{1,2},{3,4}} gives the spectrum of matrix with rows {1,2} and {3,4}.) Verify that λ2 ≤ κ(G) for this graph.
- Now let G be a general graph, and let u1 = (1,...,1) as above. Prove that L • u1 = 0 u1 = (0,...,0).
- Extra Credit: Prove that if G is not connected, then λ2 = 0. Hint: Find another eigenvector u2 with L • u2 = (0,...,0).
- Extra Credit: Make some rubber-band graphs to hook onto the exterior triangle on my board. For example, make the
icosahedron: 12−3 = 9 internal vertices (little rings) and 30−3 = 27 rubber-band edges.
It would be especially interesting to compare the experiment with the exact analytic solution computed above.
Practical considerations.- You have to break in the rubber bands with a few dozen stretches to make their forces uniform.
- To get an accurate model of the Hooke forces, you have to use smaller rubber-bands for the innermost edges, since their natural length is not zero, and they would go slack when their ends are too close.
- In such an arrangement, are there the same Hooke forces from all the different kinds of rubber bands? You might have to use thicker bands, or double up, to make the forces uniform...
- Proof of Tutte's Theorem.
- In class, we proved the following lemmas, which are part of the proof that an equilibrium position forms a good drawing of any 3-connected planar G, decomposing the exterior into non-overlapping convex polygons.
- We assume an equilibrium position with mobile internal vertex positions v1,..., vk and external vertices vk+1,..., vn forming a fixed convex polygon.
- Lemma 1: Each internal vertex vi is the centroid (vector average) of its neighboring vertices: vi = 1⁄n ∑j∈N(i) vj.
- Lemma 2: No vertex can have all its neighbors on the same line ℓ.
We proved this by defining a Y-graph as the union of three independent paths in G, joined at a single common endpoint. We showed that if all the neighbors of v are on a line ℓ, then we can construct three Y-graphs, disjoint except for their common leaf vertices a,b,c: one Y-graph on ℓ, one above ℓ, one below ℓ. But this is a contradiction, since these Y-graphs form a subdivision of the complete bipartite graph K3,3, which cannot exist in a planar G by Kuratowski's Theorem.
- For the equilibrium positions found in HW 4/7 #1, 2 and in Prob 1 above, check that each internal vertex vi is the centroid of its neighbors.
- Extra Credit: Find a counter-example to Lemma 2 if G is allowed to be only 2-connected: that is, find a 2-connected graph whose equilibrium position does have an internal vertex with all neighbors on a single line.
- Extra Credit: In the proof of Lemma 2, we assumed that all neighbors of the internal vertex vi lay on the line ℓ. One case we skipped is if some of these neighbors of vi are fixed external vertices vj, v'j: these must be of maximum or minimum height with respect to ℓ, so it would not be possible to construct three Y-graphs as before, nullifying the previous contradiction of Kuratowski's Theorem. Nevertheless, why is this case impossible?
- Partial Laplacian matrix to find equilibrium positions
- From the definiton of matrix multiplication, we immediately see the equivalence of the matrix equation and the linear system for equilibrium position.
- For the chiral hexahedron graph (6 vertices, with external vertices an equilateral triangle), we compute x-coordinates:
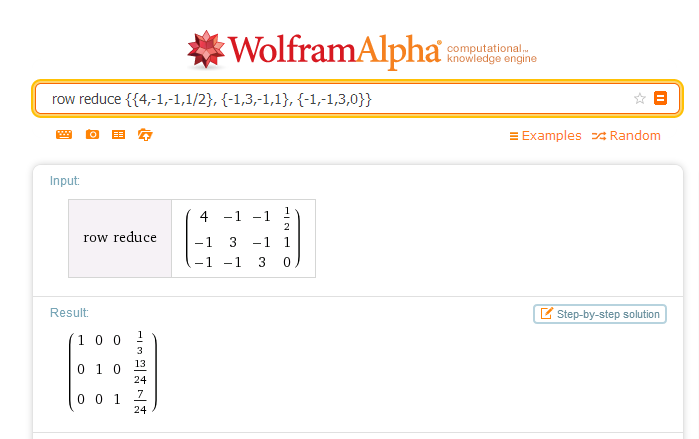
Then y-coordinates:
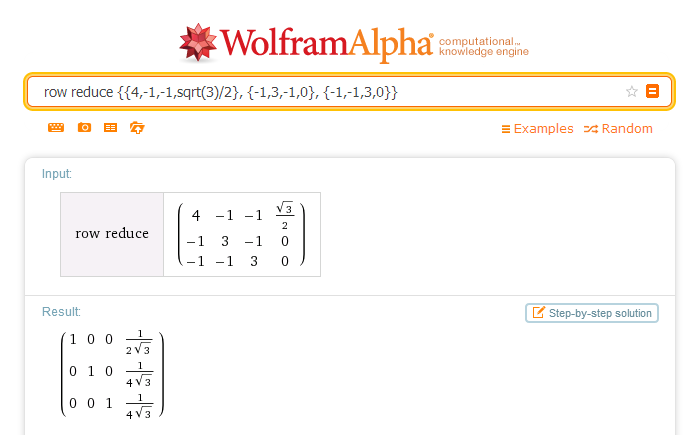
Thus:(x1, y1) = (1⁄3, 1⁄2√3 ), (x2, y2) = (13⁄24, 1⁄4√3 ), (x3, y3) = (7⁄24, 1⁄4√3 ).
- Full Laplacian
- The adjacency matrix A and the (full) Laplacian L, for the 5-vertex graph in
HW 4/7 #1:
0 1 1 1 1 1 0 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 4 −1 −1 −1 −1 −1 3 0 −1 −1 −1 0 3 −1 −1 −1 −1 −1 4 −1 −1 −1 −1 −1 4 - Wolfram Alpha gives the eigenvalues of L as:
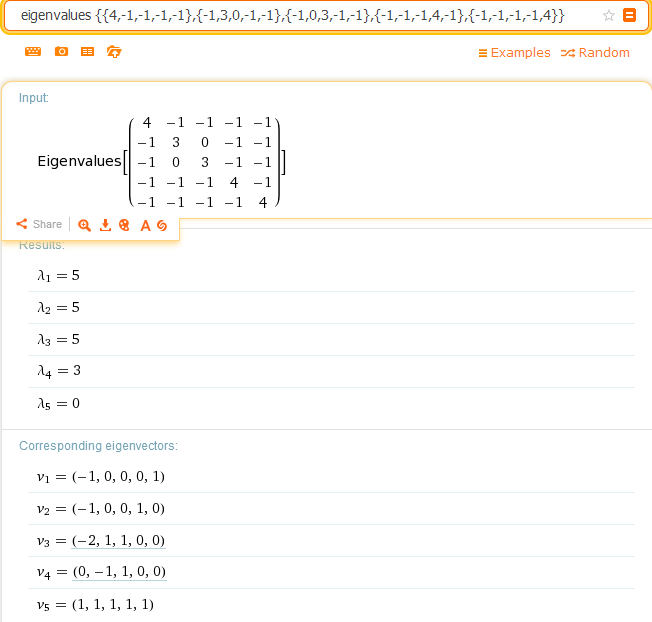
Note that they index the eigenvalues from largest to smallest, so that they write λ4 instead of our notation λ2. That is, the second smallest eigenvalue is: λ2 = 3. This is equal to κ(G), the index of connectivity; and also equal to δ(G), the smallest deg(v) of G.
- The adjacency matrix A and the (full) Laplacian L, for the 5-vertex graph in
HW 4/7 #1:
- 4/14: Begin Maxwell's Lifting Theorem
Reading:- Notes
- My lectures follow Richter-Gebert pp. 133−139: this part is pretty readable.
- Wikipedia on the Laplace equation and the Dirichlet problem, which is a continuous analog of our rubber-band equations.
- Consider the simplest 3-connected planar graph, G = Pyr(3) = K4, the tetrahedron graph,
with equilibrium position:
- Find the vectors q1, q2, q3 for the 3 internal regions, starting with q1 = (0,0,0).
- Find q3 in two ways, by starting with q1 = (0,0,0) and following both paths of neighboring regions: verify that the same q3 is produced. Can you explain why? (Hint: It has to do with the special positions of vi.)
- What is the effect of raising vi to (vi,1) before taking cross products? Why do we get downward-pointing qi's? Try to picture the geometry involved. Hint: Review the right-hand rule for the cross-product.
- Find h1,..., h4, the heights of all vertices. Again, compute h1 in three ways, corresponding to all 3 regions containing v 1: check that you get the same answer each time.
- Sketch the polyhedron with corners (vi, hi).
- 4/16: Maxwell's Lifting Theorem
Reading:- Notes
- Richter-Gebert pp. 133−139. Lemmas 13.1.1−13.1.4 correspond to our Lemmas 1,2,3.
- Let G be the chiral hexahedron graph from HW 4/7 #2
and HW 4/11 #1b.

- For the external vertices, instead of the equilateral triangle coordinates, we choose integer coordinates: v4 = (1,1), v5 = (2,0), v6 = (0,0). Work out the locations of v1, v2, v3 using the partial Laplacian matrix from HW 4/11.
- Compute Maxwell's qj vectors for the regions using the recursive formula, starting from the triangle R1 with vertices v1v4v6.
- Determine the height hi = qj • (vi,1) of each vertex, producing lifted vertices v'i = (vi, hi) of a convex polyhedron P, the convex hull of v'1,..., v'6.
- Write all the face-boundaries of P in the form q'j • v ≥ dj,
where q'j is a normal vector, v = (x,y,z) is a vector variable, and dj is a constant.
This specifies P as the vectors of height ≥ dj, with respect to the direction q'j,
as in HW 3/21.
Note: q'j is different from qj, though closely related. This corrects a mistake in the Richter-Gebert notes.
Hint: Let qj = (aj, bj, cj). The face above Rj is defined as the set of points v = (x,y,z) with (x,y) ∈ Rj, and height given by z = qj • (x,y,1), i.e.:z = ajx + bjy + cj .
- Show that P is convex, by checking that all P-vertices v'i not adjoining region Rj have q'j • u > dj.
- Prove Lemma 2: If a vertex v is a corner of two regions R,S, then the height hv is well-defined:
hv = qR • (v,1) = qS • (v,1)
- 4/18: Proof of Maxwell's Lifting Theorem
Reading:- Notes
- Richter-Gebert pp. 133−139.
- Review HW 3/21 on planes and cross-products
- Marvelous: George Hart's polyhedron gallery
- First, you need to install the VRML plugin for your browser.
- Table of contents with hundreds of polyhedra, which you can rotate (Examine mode), see close or far (Fly mode), even view from the interior (fly in past the surface).
- Canonical form of a polyhedron is the unique most well-proportioned solid for a given combinatorial type. It is defined by having all edges tangent to a given sphere, and the points of tangency having their centroid at the origin. One really neat feature is that the dual polyhedron has the same points of tangency, with each dual edge perpendicular to the original edge.
- Equivalent versions of Lemma 3 from the Notes:
- For each edge uv separating two regions S,R in G, the planes in their lifting form a surface (a lower surface of P) which is concave up (like an open book face up rather than face down).
- For any point w inside the left-hand region S, the R-height is less than the S-height.
- {(w,1), (v,1), (u,1)} is a left-handed coordinate system.
- det((w,1),(v,1), (u,1)) < 0, where ((w,1),(v,1), (u,1)) means the 3×3 matrix with row vectors (w,1),(v,1), (u,1).
- For a plane vector a = (a1,a2) ∈ R2, show that a⊥ = (−a2, a1) is 90° counter-clockwise from a. (We make the standard assumption that the y-axis is 90° counter-clockwise from the x-axis.)
- A right-handed coordinate system in the plane is a pair of non-parallel vectors {a,b} with
b counter-clockwise from a.
This means that a⊥ and b are on the same side of a, or algebraically,
a⊥ • b > 0.
Problem: Prove that {a,b} is a right-handed coordinate system if and only if det(a,b) > 0, where (a,b) is the 2×2 matrix with row vectors a,b. - A right-handed coordinate system in 3-dimensional space R3 is a triple {a,b,c} of independent vectors such
that the cross-product a×b and c are on the same side of the plane spanned by {a,b}: that is,
(a×b) • c > 0.
Problem: Prove that {a,b,c} is a right-handed coordinate system if and only if det(a,b,c) > 0. - Let S,R,u,v be as described above. Prove the crucial fact for Lemma 3: If w is to the left of the vector from u to v (i.e. on the same side as S), then {(w,1),(v,1),(u,1)} is a left-handed coordinate system (i.e. not right-handed, with det < 0).
- Finishing HW 4/16 #1e, find the equation of the top surface of the chiral hexahedron (i.e. the lid). Hint: Use HW 3/21 #2.
-
4/21: Final Review 1: Finite Difference Calculus.
Notes:- We can view a sequence (an)n≥0 as a function a : ℕ → ℝ, since to each input n ∈ ℕ (a discrete variable), it assigns an output a(n) = an. There is a close analogy with a function a(x), where x is a real number input (a continuous variable), and many familiar operations on a(x) have analogs for an.
-
The derivative operation D = d⁄dx for a(x):
Da(x) = a'(x) = limh→0 (a(x+h) − a(x))⁄h = limh→0 (a(x) − a(x−h))⁄h
Δ+an = (an+1−an)⁄1 = an+1 − an.
Δ−an = (an−an−1)⁄1 = an − an−1.
It turns out that Δ− is more useful, so we will drop the superscript, and simply denote: Δ = Δ−. -
The integral or anti-derivative operation ∫ a(x) = ∫t=0x a(t) dt
is analogous to the summation operation:
Σan = ∑i=0n ai.
-
Prove the Fundamental Theorem of Difference Calculus: Δ and Σ are inverse operations:
that is, Δan = bn
⇔
an = Σbn .
Or equivalently, for any sequence (an)n≥0, we have:
Δ(Σan) = an and Σ(Δan) = an .
-
Our main tool for analyzing a sequence is to take its generating function:
(an)n≥0 ↔ops f(x) = ∑n≥0 anxn.
- Use Prob #2 to give a generating-function proof for the Fundamental Theorem (Prob #1).
- Solve the difference equation Δ+an = an, by elementary means (just write out what it means), and also by generating functions.
Assume the initial value a0 is an arbitrary constant.
Compare to the solutions of the corresponding differential equation a'(x) = a(x). - Show that
Δ+Δ−an = Δ−Δ+an = an+1 + an−1 − 2an for n ≥ 1.
This is another way of writing the negative Laplacian operation −L (HW 4/11 #2), which adds the a-values at the neighbors of vertex n, minus the vertex-degree times the value at n. - Solve the difference equation:
Δ+Δ−an
= −an for n ≥ 1, using generating functions.
We do not assume any recurrence for n = 0; rather,
the initial values a0, a1 are arbitrary constants.
Compare to the solutions of the corresponding differential equation a''(x) = −a(x), which is a version of Hooke's Law. - Recall that, for a fixed whole number k, we have the falling-power sequence an = nk = n(n−1)⋯(n−k+1). (Also n0 = 1.) Find a simple formula for the generating function f(x) = ∑n≥0 nk xn. Hint: Start with the cases k = 1 and k = 2. Use Wilf's Rules.
- Prove
by inductionthat Δ(nk) = k(n−1)k−1 for k ≥ 1 and n ≥ 1. Hint: Is induction needed here, or can you prove it directly? - Reversing the previous problem, we have nk = k Σ(n−1)k−1, and iterating, we get nk = k! Σkcn, where Σk means perform the Σ operation k times, and cn = (n−k)0 = 1 for n ≥ k, and cn = 0 for n < k. Use this and Prob #2 as a different way to find a simple formula for the generating function f(x) = ∑n≥0 nk xn.
- Find a transformation to prove the formula:
nk = ∑i=0k {k | i}n i ,
- Newton's finite-difference Taylor series:
f(n) = ∑n≥0 ci n i , for ci = Δif(0)⁄i! . This is the interpolation polynomial passing through evenly-spaced data points (0,f(0)), (1,f(1)), . . . , (n−1,f(n−1)).
Compare to Lagrange's form of the interpolation polynomial for arbitrary data points, defined by Cramer's Rule applied to an augmented Vandermonde matrix, or by a sum of n terms with Vandermonde denominators, or by a single (n+1)×(n+1) Vandermonde determinant = 0 (extra column [f(x),1,x, . . . ,xn−1]).
-
4/23: Final Review 2:
Deletion transforms, recursive choice algorithms, generating functions
HW:- Define a language as a set W of words, which are lists of letters, according to specified rules.
In our language, a word can be any string of letters a,b, with no two consecutive a's.
We let wn be the number of allowed words with n letters.
For example, w3 = 5 counts the words:
aba, abb, bab, bba, bbb.
- A theory problem. Suppose we take two convex polyhedra P1, P2 and join them along one edge, which becomes a hinge between the two bodies. The resulting union P is clearly not convex, but still has vertices, edges, and faces.
- Is the edge-graph of P always planar? If so, explain how to draw it.
- Prove or disprove: There exists a convex polyhedron P' with the same edge-graph as P.
- Another theory problem. True or false: there exists a convex polyhedron with 100 vertices and 200 edges. Prove your answer using results we have covered.
- Words in a,b with no aa's
- Step 1: To get a recursive choice algorithm, delete the the letters up to and including the first b, if any:
Any word w ⇔ (w = ∅) or (w = a) or (w = bw' for word w') or (w = abw' for word w')
f(x) = 1 + x + x f(x) + x2 f(x).
- Step 2: To obtain information from the above formula about the coefficients wn.
- We get a recursive formula by clearing denominators and multiplying out:
(1 − x − x2) ∑n≥0 wnxn = ∑n≥0 wnxn − ∑n≥0 wnxn+1 − ∑n≥0 wnxn+2 = 1 + x .
- To obtain an exact formula, we must write f(x) as a sum of standard functions with known power series.
This form will have the same vertical and horizontal asymptotes as f(x), namely the horizontal asymptote y = 0
and the simple vertical asymptotes given by the roots of the denominator: α = ½(√5−1) and β = − ½(√5+1).
In fact, 1 − x − x2 = (1 − x/α) (1 − x/β),
and we get:
f(x) = A⁄(1 − x/α) + B⁄(1 − x/β)
A = limx→α (1 − x/α) f(x) = limx→α (1 − x/α)(1+x)⁄(1 − x/α)(1 − x/β) = (1+α)⁄(1 − α/β) = (5+3√5)⁄10 ,
- To get an asymptotic formula, we extract the contribution of the vertical asymptote closest to the the origin, namely x = α. That is, wn ≈ A/αn. Since |1/β| < 1 < |1/α|, the second term of the exact formula is a tiny correction.
- We get a recursive formula by clearing denominators and multiplying out:
- Step 1: To get a recursive choice algorithm, delete the the letters up to and including the first b, if any:
- Hinged polyhedron.
- Given a planar graph G with an internal region R,
we can invert R, flipping all the edges and vertices outside R to the inside.
(Geometrically, if we draw G so that R is a unit circle, we flip each point outside R to
the reciprocal of its radius.) In the resulting picture, R becomes the outside region.
Now, given the graphs of P1, P2, each with a specified edge, we can do inversion so that each edge is on the exterior of the drawing. Now we can join these edges vertex-to-vertex in the plane, giving a planar drawing of the edge-graph of P. - The above graph could not be the edge-graph of a convex polyhedron, because it is not 3-connected: removing the 2 vertices of the join-edge clearly disconnects the graph. But Steinitz's Theorem states that the edge-graph of any convex polyhedron is 3-connected.
- Given a planar graph G with an internal region R,
we can invert R, flipping all the edges and vertices outside R to the inside.
(Geometrically, if we draw G so that R is a unit circle, we flip each point outside R to
the reciprocal of its radius.) In the resulting picture, R becomes the outside region.
- Can there be a convex polyhedron with n = 100 vertices and q = 200 edges?
One simple test is whether q exceeds the number of edges in a maximal planar graph:
200 = q ≤ 3n−6 = 294, which does not disqualify n,q.
Steinitz's Lemma gives the real answer: a simple numerical criterion for the f-vectors of all convex polyhedra. Euler's Formula gives r = 2−n+q = 102, which satisfies:100 = n ≤ 2r−4 = 200 and 102 = r ≤ 2n−4 = 196.
- Define a language as a set W of words, which are lists of letters, according to specified rules.
In our language, a word can be any string of letters a,b, with no two consecutive a's.
We let wn be the number of allowed words with n letters.
For example, w3 = 5 counts the words:
- 4/25: Final Review 3
HW: Here is a "greatest hits" list from our HW, keyed to the test topics.
Note: You should be able to state the definitions and theorems listed below, and apply them to particular cases.- Twelvefold Way
- HW 1/10 #1. Different data structures describing functions.
- Transformations
- Power series manipulations
-
HW 1/29 #2. Practice with Wilf's Rules.
- Ordinary and exponential generating functions, combinatorial families −−−−−− Midterm −−−−−−
- Trees, recursive families, Lagrange Inversion Formula
- Dlog method and recurrences
- Otter's Formula for unrooted trees
- Tree proofs
- Math 481 HW 11/6 #1, 2. Definitions and properties of trees.
- Planar graphs, Euler's Formula
- HW 4/4 #1. Polyhedral graph formulas.
- Graph connectivity, Menger's Theorem
- HW 3/31 #2. Augmenting path algorithm for Menger's Theorem.
- Polyhedra, standard examples, vector geometry
- Steinitz Theorem, Balinski theorem
- Tutte's Rubber Band Model
- HW 4/11 #1. Laplacian matrix for computing equilibrium position.
- Maxwell's Lifting Theorem
- Twelvefold Way